POLITECHNIKA WARSZAWSKA

PODSTAWY KONSTRUKCJI URZĄDZEŃ PRECYZYJNUCH

PROJEKT 1

Temat: MODUŁ STOLIKA LINIOWEGO - 23

Wykonał: Dariusz Kidacki Gr. UL

Prowadzący: dr inż. Zbigniew Kusznierewicz

PROJEKT 1

Temat: MODUŁ STOLIKA LINIOWEGO - 23

Wykonał: Dariusz Kidacki, Gr.UL

1. KRÓTKI OPIS ZADANIA

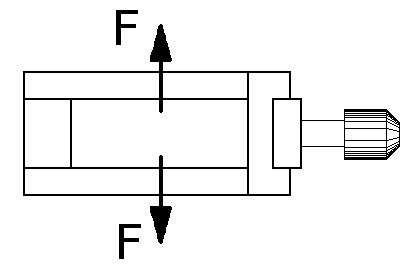
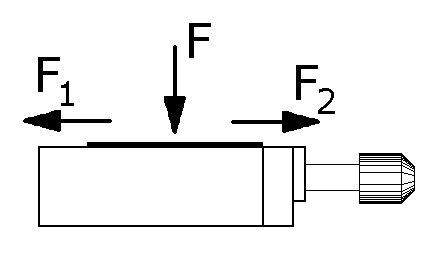
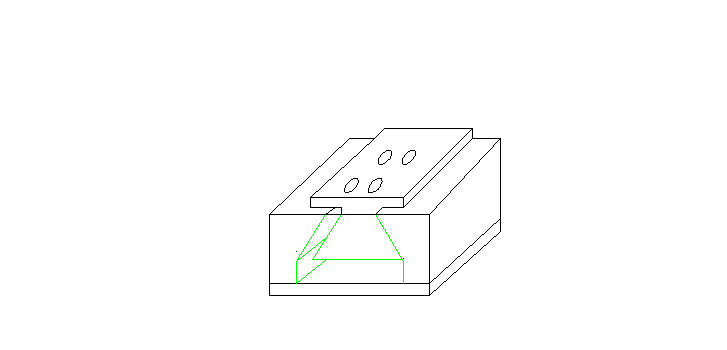
Zadaniem moim było sporządzenie projektu Modułu Stolika Liniowego o wymiarach 50x50 (wymiary podane w milimetrach), który porusza się wzdłuż jednej osi (posiada jednak możliwość pozwalającą dołączyć inne podobne zespoły dzięki którym możliwy będzie ruch w płaszczyźnie XY a nawet po odpowiednich modyfikacjach w płaszczyznach XYZ). Ruch stolika wywoływany jest przez poruszającą się głowice śruby mikrometrycznej. Stolik porusza się na prowadnicy typu jaskółczy ogon. Ze względu na zadane na zadane obciążenia : F = 50 [N], F₁ = 10 [N], F₂ = 25 [N] (patrz rysunek poniżej) zdecydowałem się użyć sześć układów wałków umieszczonych w separatorze. Poniżej zamieszczam także rysunek poglądowy stolika.

2. OBLICZENIA KONSTRUKCYJNE

• Obliczam długość separatora:

S = a - 0.5L gdzie: a - długość stolika, L - zadany zakres ruchu

S = 40 [mm]

• Obliczam siłe kasującą luz:

F_w = k*F gdzie: k - współczynnik zawierający się w przedziale(0.2 -0.4)

F - zadana siła

F_w = 15 [N] przyjąłem k = 0.3

• Obliczam wartości składowych od siły F_w działających na poszczególne wałeczki:

Z zależności trygonometrycznych wynika:

F_sw = 18,31 [N]

F_nw = 10,5 [N]

F_max1 = 0.5F + F_nw = 35,5 [N]

F_max2 = F_sw + F/sin55 =79,35 [N]

Z obliczeń wynika, że na wałek drugi będzie przenosił dużo większe obciążenia

Wybieram wałeczki o wymiarach r = 1 [mm] i l = 4.8 [mm]

• 
  Obliczam maksymalne obciążenie jakie może przenieść pojedyńczy zespół wałków ze wzoru HERTZA

P_HMAX = 0.564 [F_n / {r * l*((1 - v₁² / E₁) + (1 - v₂² / E₂))²}]^1/3 = 16 [N]

Gdzie: F_n - maksymalna siła jaką może przenieść wałek

v₁, v₂ - liczba Poissona dla stali

E₁, E₂ - moduł sprężystości prowadnicy i kulki

Opierając się na tych obliczeniach zakładam konieczność użycia sześciu zespołów wałków ponieważ 6*16[N] > 79,35 [N]

• Obliczam minimalną siłę potrzebną do przesunięcia stolika

P_min > (F₁ + T_c ) gdzie: F₁ - zadane obciążenie, T_c - całkowite

opory ruchu,

m_obl - wsp. tarcia zawarty w (0.0015 - 0.003)

T_c = m_obl*F_max1*(1 + cos55/sin55) + 2*m_obl*F_w*(1 + cos55/sin55)

T_c = 0.67 [N]

Więc do obliczeń przyjąłem m_obl =0,0025

P_min > 5,67 [N]

• Obliczenia konstrukcyjne związane ze sprężyną

P_pocz > P_min przyjmuje siłę początkową P_pocz = 7 [N]

P_k = (1.3 - 2)*P_pocz siła końcowa będzie równa czternastu Niutonom

P_k = 2*7 [N] = 14[N]

P_gr = P_k / (1 - si) gdzie współczynnim si zawiera się w przedziale(0.05 - 0.1)

Obieram si równe 0.08

P_gr = 15.22 [N]

Ponieważ zakładam użycie sprężyny z napięciem początkowym zatem

P₀ < P_gr / 3

P₀ = 5 [N]

Obliczam strzałkę wydłużenia f

f_z = L(P_k - P₀) / (P_k - P_pocz) zatem

f_z = 9.6 [mm]

Obliczam strzałkę wydłużenia f₀

f₀ = L*P₀ / (P_k - P_pocz) zatem

f₀ =5.4 [mm]

Obliczam strzałkę wydłużenia całkowitego

f = f_z +f₀ zatem

f =15 [mm]

Zakładam wskaźnik sprężyny w = 10. Wskaźnik powinien zawierać się w przedziale (7 - 12)

w = D /d gdzie: D - Średnia średnica sprężyny, d - średnica drutu sprężyny

Obliczam współczynnik poprawkowy - k ze wzoru:

k = 1 +5/4(1/w) + 7/8(1/w)² + (1/w)³

k = 1.172

Obliczam średnice drutu d ze wzoru:

d = 8*P_k*w*k / k_s*Pi gdzie: k_s - dopuszczalne naprężenie na skręcanie,

przyjmuje k_s równe 600[Mpa], Pi ~ 3.14

d = 0.74[mm]

Zaokrąglam w górę do najbliższej wartości katalogowej czyli d = 0,8[mm]

Obliczam średnią średnice sprężyny D ze wzoru

D = w*d zatem

D = 6,4 [mm]

Obliczam ilość zwojów czynnych Z_c ze wzoru:

Z_c = G*d*f / 8*P_k*w³ gdzie: G wynosi 8*10⁴ [Mpa]

Z_c = 6.64

Przyjmuje więc, że jest 7 zwojów czynnych. Dodatkowo używam jednego (po połowie na każdą ze stron ) zwojów jako mocowanie do śrub.

Obliczam wydłużenie sprężyny nieobciążonej

l₀ = Z_c* d + z gdzie: z = D (dodatkowy zwój na mocowanie)

l₀ = 12[mm]

Obliczam wydłużenie na końcu skoku roboczego l_k

l_k = l₀ - f₀ +f zatem

l_k = 22 [mm]

Obliczam długość sprężyny na początku skoku roboczego l₁

l₁ = l_k - L zatem

l₁ = 17[mm]

Obliczam z jaką działa głowica śruby mikrometrycznej na stolik

Ze wzoru Hertza mamy:

P_HMAX = 0.578 [F_n / {r ²((1 - v₁² / E₁) + (1 - v₂² / E₂))²}]^1/3 = 7 [N]

Gdzie r jest promieniem czaszy którą zakończona jest głowica mikrometryczny i

Wynosi:1,5[mm]

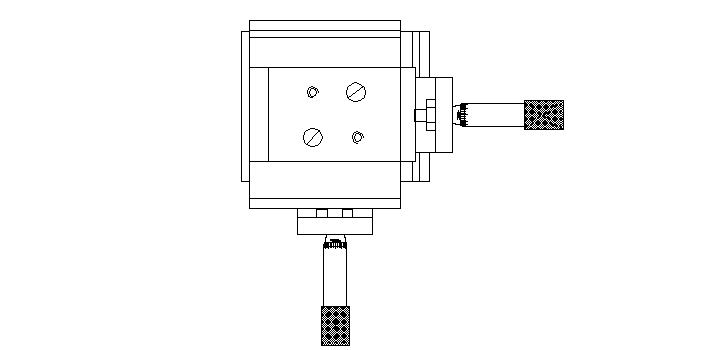
3. MONTAŻ DRUGIEGO MODUŁU

W celu stworzenia manipulatora mającego możliwość poruszania się wzdłuż drugiej osi tworzącej płaszczyznę w której porusza się blat stolika należy:

• Obydwa stoliki cofnąć do położenia początkowego (tzn. śruba mikrometryczna nie wywiera nacisku na stolik).

• Położyć jeden stolik na drugim (`na krzyż' tzn. aby jeden był względem drugiego obrócony o90[stopni])) tak aby otwory wywiercone w blatach pokrywały się .

• Za pomocą dołączonych śrub przytwierdzić jeden stolik do blatu drugiego.

1. UWAGI KOŃCOWE

Blokada ruchu w powyższym projekcie stolika liniowego nie jest konieczna ponieważ zastosowałem śrubę mikrometryczną o zakresie ruchu pokrywającym się całkowicie z zadanym zakresem ruchu stolika. Biorąc jednak pod uwagę możliwość niedokładnego zamocowania śruby mikrometrycznej w przystawce( co wydaje się mało prawdopodobne ze względu na konstrukcje przystawki przystosowanej specjalnie do obranej głowicy mikrometrycznej ) zaplanował milimetr luzu pomiędzy końcowym położeniem stolika a płyta zamykającą konstrukcje.

Wszelkie wzory jak również zakresy stałych użytych bo powyższych obliczeń zaczerpnięte są z wykładu prowadzonego przez pana prof. dr hab. Waldemara Oleksiuka jak również z ćwiczeń projektowych prowadzonych przez pana prof. dr. hab. Zygmunta Rymuze .

---