Zbieżność całek postaci 1 rodzaju
![]()
Niech a>0. Wtedy
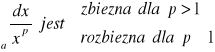
Kryterium porównawcze
Jeżeli
1. 0 ≤ f(x) ≤ g(x) dla każdego x ∈ [a,∞),
2. funkcje f i g są całkowalne na przedziałach [a,T] dla T>a,
3. całka 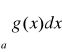
jest zbieżna
to całka 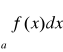
jest zbieżna.
Kryterium ilorazowe
Niech funkcje dodatnie f i g będą całkowalne na przedziałach [a,T] dla każdego T>a oraz niech ![]()
, gdzie 0<k<∞. Wówczas
całka 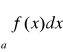
jest zbieżna ⇔ całka 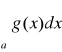
jest zbieżna.
Zbieżność bezwzględna całek niewłaściwych pierwszego rodzaju
Niech funkcja f będzie całkowalna na przedziałach [a,T] dla każdego T>a. Całka 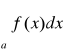
jest zbieżna bezwzględnie 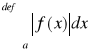
jest zbieżna.
O zbieżności całek 2 rodzaju![]()
Niech b>0. Wtedy całka niewłaściwa 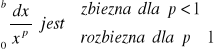
.
Warunek konieczny zbieżności szeregu
Jeżeli szereg ![]()
jest zbieżny, to ![]()
.
Zbieżność szeregów postaci ![]()
Szereg 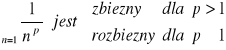
Kryterium d'Alemberta
1. Jeżeli 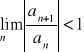
, to szereg ![]()
jest zbieżny.
2. Jeżeli 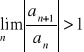
, to szereg ![]()
jest rozbieżny.
Kryterium Cauchy'ego
1. Jeżeli ![]()
, to szereg ![]()
jest zbieżny.
2. Jeżeli ![]()
, to szereg ![]()
jest rozbieżny
Leibniza o zbieżności szeregu naprzemiennego
Jeżeli
1. ciąg (bn) jest nierosnący od numeru n0∈N,
2. ![]()
to szereg naprzemienny
![]()
jest zbieżny.
Promień zbieżności szeregu potęgowego
Promieniem zbieżności szeregu potęgowego ![]()
nazywamy liczbę R określoną równością:
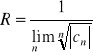
,
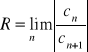
Cauchy'ego - Hadamarda
Niech 0 < R < ∞ będzie promieniem zbieżności szeregu potęgowego ![]()
. Wtedy szereg ten jest:
a) zbieżny bezwzględnie w każdym punkcie przedziału (x0 - R , x0 + R),
b) rozbieżny w każdym punkcie zbioru (-∞ , x0 - R )∪(x0 + R, ∞).
Def. 4.1.1 (pochodne cząstkowe pierwszego rzędu)
Niech funkcja f będzie określona na obszarze D ⊂ R2 oraz niech (x0,y0) ∈ D. Pochodną cząstkową pierwszego rzędu funkcji f względem x w punkcie (x0,y0) określamy wzorem:
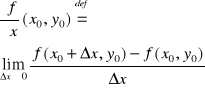
Dla y to samo.
Pochodne cząstkowe drugiego rzędu
Niech funkcja f ma pochodne cząstkowe ![]()
, ![]()
na obszarze D ⊂ R2 oraz niech (x0,y0) ∈ D. Pochodne cząstkowe drugiego rzędu funkcji f w punkcie (x0,y0) określamy wzorami:
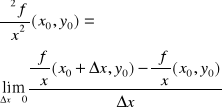
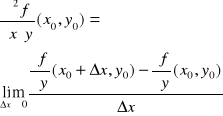
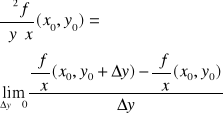
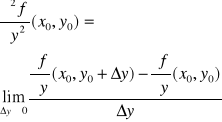
.
Równanie płaszczyzny stycznej do wykresu funkcji w punkcie (x0,y0,z0), gdzie ![]()
, ma postać:
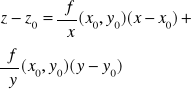
Różniczka funkcji
Różniczką funkcji f w punkcie (x0,y0) nazywamy funkcję zmiennych ![]()
, ![]()
określoną wzorem:
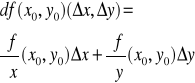
.
Zastosowanie różniczki funkcji do obliczeń przybliżonych
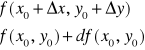
Zastosowanie różniczki funkcji do szacowania błędów pomiarów
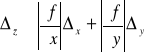
O pochodnej funkcji złożonej
![]()
Pochodna kierunkowa funkcji
niech ![]()
będzie wersorem na płaszczyźnie. Pochodną kierunkową funkcji f w punkcie (x0,y0) w kierunku wersora ![]()
określamy wzorem:
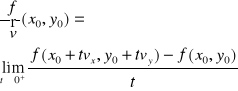
Gradient funkcji
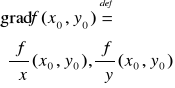
Pochodna kierunkowa
![]()
Warunek konieczny istnienia ekstremum)
![]()
![]()
.
Warunek wystarczający istnienia ekstremum
1. funkcja f ma ciągłe pochodne cząstkowe rzędu drugiego na otoczeniu punktu (x0,y0),
2. ![]()
,
3. 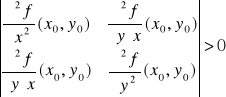
.
a) minimum lokalne właściwe, gdy ![]()
b) maksimum lokalne właściwe, gdy ![]()
O istnieniu i różniczkowalności funkcji uwikłanej
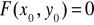
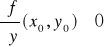
.
Wtedy na pewnym otoczeniu punktu x0 istnieje jednoznacznie określona funkcja uwikłana y = y(x) spełniająca warunki:
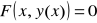
dla każdego x z tego otoczenia,y(x0) = y0,
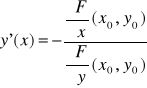
dla każdego x z tego otoczenia.
O ekstremach funkcji uwikłanej
niech
![]()
,
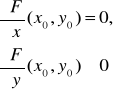
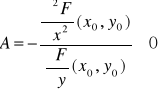
.
Wtedy funkcja uwikłana y = y(x) określona przez równanie F(x,y) = 0 ma w punkcie (x0,y0) ekstremum lokalne właściwe i jest to:
minimum, gdy A > 0
maksimum, gdy A < 0.
Równanie stycznej do krzywej określonej równaniem F(x,y)=0, w punkcie (xo,yo)
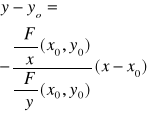
Wyszukiwarka