WEWNĄTRZSZKOLNY KONKURS MATEMATYCZNY
LIGA ZADANIOWA
etap 5 - odpowiedzi
Klasy I
5. Świeże grzyby zawierają 90% wody, suszone tylko 12%. Ile świeżych grzybów trzeba ususzyć, aby otrzymać 5 kg suszonych grzybów?
Odp. Grzyby - świeże jak i suszone - składają się z wody i „masy suchej”.
Skoro świeże grzyby zawierają 90% wody, to zawierają 100% - 90 % = 10 % „masy suchej”. Grzyby suszone zawierają 12 % wody, więc „masy suchej” jest 100% - 12 % = 88 %.
Niech: x - poszukiwana waga świeżych grzybów.
W wyniku suszenia grzybów waga „masy suchej” nie zmienia się. Stąd wynika, że:
10 % z x = 88 % z 5
![]()
![]()
![]()
![]()
![]()
Odp. Aby otrzymać 5 kg suszonych grzybów trzeba ususzyć 44 kg świeżych grzybów.
Klasy II
5. Dzieląc liczbę 100 przez pewną liczbę naturalną ![]()
otrzymujemy resztę 4, a dzieląc liczbę 90 przez tę samą liczbę ![]()
otrzymujemy resztę 18. Znajdź liczbę ![]()
.
Odp. Przypomnijmy sobie dzielenie z resztą.
Niech ![]()
, ![]()
, ![]()
, ![]()
- dowolne liczby naturalne. Mówimy, że w wyniku dzielenia liczby ![]()
przez ![]()
otrzymujemy iloraz ![]()
i resztę ![]()
(![]()
i ![]()
), jeżeli ![]()
.
Z warunków zadania wynika, że istnieją takie dwie liczby naturalne ![]()
i ![]()
takie, że:
![]()
i ![]()
i ![]()
Odejmując oba równania stronami otrzymujemy: ![]()
![]()
![]()
![]()
![]()
.
Ponieważ lewa strona równania jest podzielna przez ![]()
, to i prawa strona jest podzielna przez ![]()
. Czyli ![]()
jest dzielnikiem 24.
Dzielniki 24 to: 1, 2, 3, 4, 6, 8, 12, 24.
Możemy odrzucić wszystkie liczby mniejsze od 18. Zostaje nam tylko 24.
Odp. 24.
Klasy III
5. Punkt E leży na ramieniu BC trapezu ABCD, w którym ![]()
. Udowodnij, że ![]()
.
Odp.
Narysujmy rysunek pomocniczy. Wprowadziliśmy oznaczenia:
![]()
, ![]()
, ![]()
, ![]()
, ![]()
.
Teza z naszego twierdzenia brzmi teraz następująco: ![]()
.
W dowodzie będziemy korzystali z własności trójkątów i trapezów oraz miary kąta.
W trapezie suma miar kątów leżących przy tym samym ramieniu jest równa
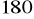
, czyli: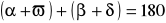
.Suma miar kątów trójkąta jest równa
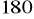
, czyli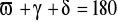
.
Z (2) wynika, że ![]()
.
Podstawiając do (1) otrzymujemy: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
.
Co należało udowodnić.
Zadania i rozwiązania znajdziecie na http://chomikuj.pl/matematyka4lo/Liga+zadaniowa
A
B
C
D
E
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka