Państwowa Wyższa Szkoła Zawodowa
im. Prezydenta Stanisława Wojciechowskiego
w Kaliszu
Instytut Politechniczny
Inżynieria Środowiska
Laboratorium z Mechaniki Płynów
Opadanie cząstek ciał stałych w płynach
Przygotowali:
Cel ćwiczenia.
Celem ćwiczenia jest zapoznanie się z doświadczalną metodą wyznaczania współczynników oporów przepływu.
Wprowadzenie.
Opadanie pojedynczej kulistej cząstki w przestrzeni nieograniczonej.
Analiza ruchu cząstek w płynie w przestrzeni nieograniczonej prowadzi do wniosku, że prędkość, która początkowo rośnie (cząstka w ciągu pewnego krótkiego czasu opada ruchem przyśpieszonym), po pewnym czasie ustala się i dalej pozostaje niezmienna. Dzieje się tak na skutek tego, że dalszemu wzrostowi prędkości opadania przeciwstawia się rosnący opór ośrodka płynnego. Od momentu, gdy siła ciężkości cząstki zrówna się z siłą oporów ośrodka - prędkość, z jaką opada cząstka będzie stała.
Opadanie pojedynczej kulistej cząstki w przestrzeni ograniczonej.
Prędkość cząstki podczas jej grawitacyjnego opadania w przestrzeni ograniczonej (w cylindrze) jest mniejsza niż w przestrzeni nieograniczonej. Związane jest to z istnieniem przepływu cieczy w górę wokół opadającej cząstki. Ruch ten jest hamowany na skutek oddziaływania ścianki naczynia.
Obliczenia.
Wzory:
Liczba Reynoldsa:
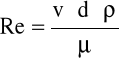
gdzie: v - prędkość opadania cząstek,
d - średnica opadającej cząstki,
ρ - gęstość płynu,
μ - lepkość płynu.
Przeliczanie prędkości opadania cząstki w przestrzeni ograniczonej na prędkość opadania w przestrzeni nieograniczonej:
dla 1 < Re < 50:
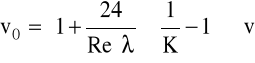
gdzie: v0 - prędkość opadania cząstki w przestrzeni nieograniczonej,
Re - liczba Reynoldsa,
λ - współczynnik oporów przepływu,
K - oblicza się ze wzoru:
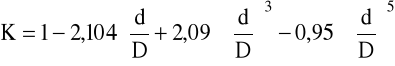
D - średnica cylindra.
dla Re > 100
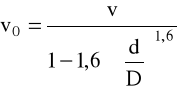
Współczynnik oporu przepływu:
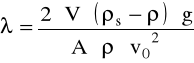
gdzie: V - objętość cząstki,
A - pole powierzchni rzutu cząstki na płaszczyznę prostopadłą do kierunku opadania,
ρS - gęstość ciała stałego,
g - przyśpieszenie ziemskie.
Obliczenia dla kulki o średnicy 4,5mm.
Dane: d = 0,0045m, D = 0,6m, V = 4,77·10-8m3, A = 1,59·10-5m2, ρS = 2500kg/m3, K = 0,984.
a) dla wody:
v = 0,305m/s, ρ = 1000kg/m3, μ = 1·10-3Pa·s.
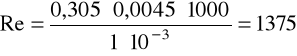
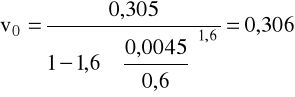
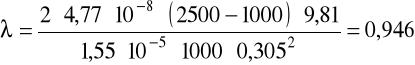
dla glikolu:
v = 0,201m/s, ρ = 1120kg/m3, μ = 40·10-3Pa·s.
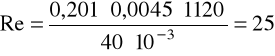
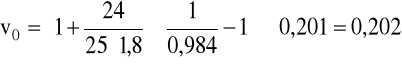
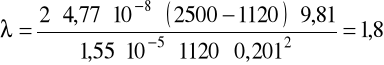
dla oleju:
v = 0,13m/s, ρ = 900kg/m3, μ = 60·10-3Pa·s.
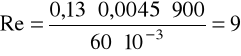
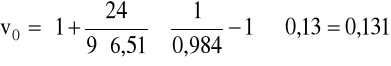
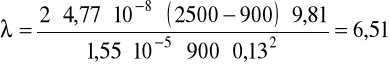
Obliczenia dla kulki o średnicy 5,2mm.
Dane: d = 0,0052m, D = 0,6m, V = 7,36·10-8m3, A = 2,12·10-5m2, ρS = 2500kg/m3, K = 0,982.
a) dla wody:
v = 0,327m/s, ρ = 1000kg/m3, μ = 1·10-3Pa·s.
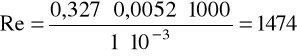

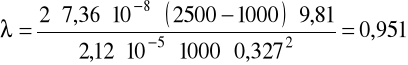
b) dla glikolu:
v = 0,254m/s, ρ = 1120kg/m3, μ = 40·10-3Pa·s.
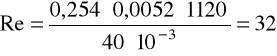
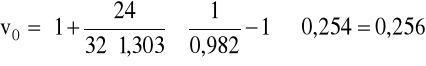
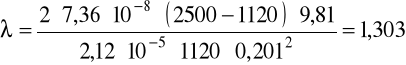
c) dla oleju:
v = 0,176m/s, ρ = 900kg/m3, μ = 60·10-3Pa·s.
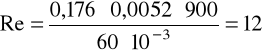
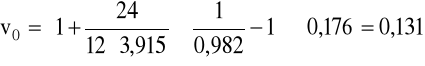
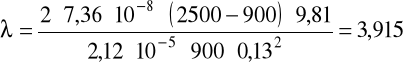
Obliczenia dla kulki o średnicy 8,5 mm.
Dane: d = 0,0085m, D = 0,6m, V = 3,22·10-7m3, A = 5,67·10-5m2, ρS = 2500kg/m3, K = 0,970.
a) dla wody:
v = 0,475m/s, ρ = 1000kg/m3, μ = 1·10-3Pa·s.
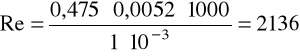

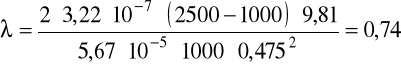
b) dla glikolu:
v = 0,378m/s, ρ = 1120kg/m3, μ = 40·10-3Pa·s.
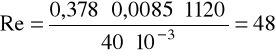
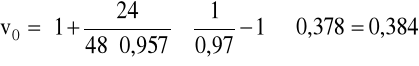
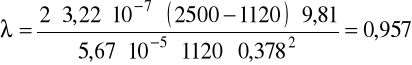
c) dla oleju:
v = 0,289m/s, ρ = 900kg/m3, μ = 60·10-3Pa·s.
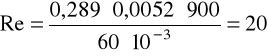
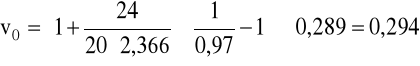
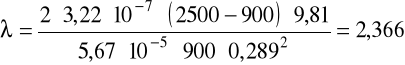
Obliczenia dla kulki o średnicy 15,7mm.
Dane: d = 0,0157m, D = 0,6m, V = 2,03·10-6m3, A = 1,94·10-4m2, ρS = 2500kg/m3, K = 0,945.
a) dla wody:
v = 0,619m/s, ρ = 1000kg/m3, μ = 1·10-3Pa·s.
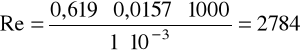
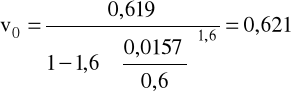
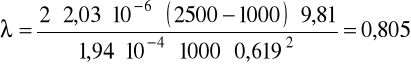
b) dla glikolu:
v = 0,586m/s, ρ = 1120kg/m3, μ = 40·10-3Pa·s.
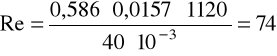
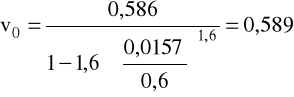
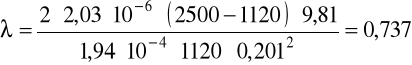
c) dla oleju:
v = 0,516m/s, ρ = 900kg/m3, μ = 60·10-3Pa·s.
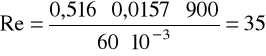
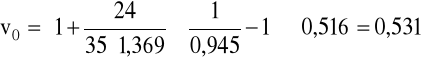
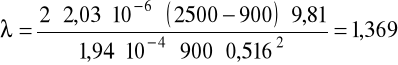
Wykresy.
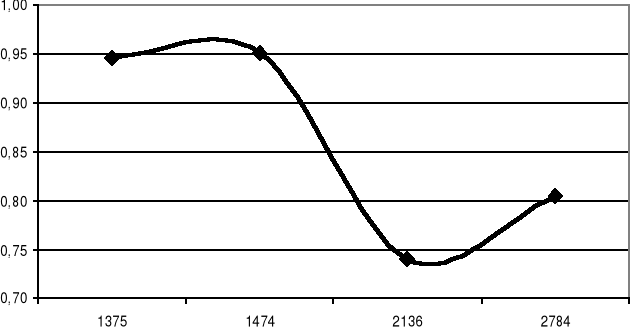
Wykres zależności współczynników oporu przepływu od liczby Reynoldsa dla wody.
2. Wykres zależności współczynników oporu przepływu od liczby Reynoldsa dla glikolu.
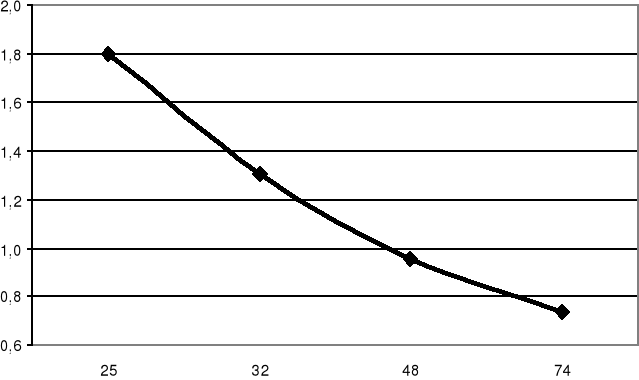
3. Wykres zależności współczynników oporów przepływu od liczby Reynoldsa dla oleju.
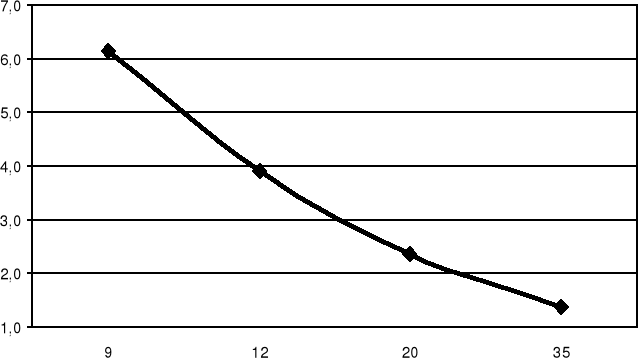
V. Wnioski.
Na podstawie dokonanych doświadczeń oraz na podstawie dokonanych obliczeń można stwierdzić, że współczynniki oporów przepływu λ rosną wraz ze spadkiem liczby Reynoldsa oraz ze wzrostem gęstości i lepkości cieczy.
Porównując otrzymane wykresy zależności współczynników oporów przepływu λ od liczby Reynoldsa z wykresem na rys. 1 zamieszczonym w instrukcji do ćwiczenia można stwierdzić, że przebieg tych wykresów jest do siebie zbliżony. Dla niskich wartości liczby Reynoldsa zależność ta ma postać liniową, dopiero dla wyższych wartości liczby Reynoldsa następują zakłócenia w przebiegu wykresu.
2
Liczba Reynoldsa Re
Współczynnik oporów przepływu λ
Liczba Reynoldsa Re
Współczynnik oporów przepływu λ
Liczba Reynoldsa Re
Współczynnik oporów przepływu λ
Wyszukiwarka