PRZEPŁYWY MIĘDZYGAŁĘZIOWE.
Jedną z metod analizy zależności występujących w procesach tworzenia i podziału produkcji materialnej są metody przepływów międzygałeziowych (analizy nakładów i wyników, analizy input-output).
Elementarnym opisem układu jest tutaj tzw.
tablica przepływów międzygałęziowych
(tutaj: ujęcie wartościowe w [zł])
dział |
produkcja globalna |
przepływy międzygałęziowe [xij] |
produkcja finalna |
||
|
Xi |
xi1 |
xi2 |
xi3 |
xi |
1 |
800 |
400 |
200 |
120 |
80 |
2 |
1000 |
160 |
400 |
120 |
320 |
3 |
600 |
160 |
200 |
180 |
60 |
koszty materiałowe |
1940 |
720 |
800 |
420 |
460 |
płace Vj |
345 |
60 |
150 |
135 |
x |
zyski Mj |
115 |
20 |
50 |
45 |
x |
wartość dodana Dj |
460 |
80 |
200 |
180 |
x |
produkcja globalna Xj |
2400 |
800 |
1000 |
600 |
x |
Podstawowe wielkości występujące w bilansie PM zdefiniowano w boczku i główce powyższej tablicy PM.
Matematyczny opis powiązań ujętych w tablicy PM nosi nazwę modelu PM,
(modelu nakładów i wyników, modelu input-output)
Podstawowe założenia dla rozpatrywanej tutaj najprostszej wersji modelu PM to:
1. układ daje się podzielić na n wzajemnie ze sobą powiązanych działów (gałęzi),
2. układ jest układem odosobnionym, tj. bez powiązań zewnętrznych.
Fudamentalnym pojęciem modelu PM jest pojęcie
współczynnika techniczno-finansowego (kosztów)
![]()
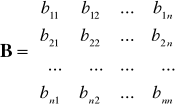
Interpretacja: jaka wartość produkcji działu "i" musi być zaangażowana w wytworzenie produkcji o wartości 1 zł w dziale "j"
W przykładowym układzie 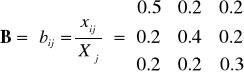
Układ równań bilansowych produkcji globalnej (Xi)
Bilans podziału produkcji globalnej
wartość produkcji globalnej =
zużycie produkcyjne + produkcja finalna (końcowa)
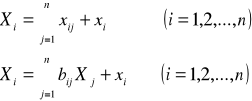
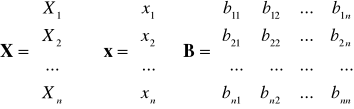
Układ równań bilansowych w zapisie macierzowym
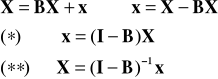
() Macierz (I-B) nazywana jest macierzą struktury techniczno-finansowej (lub macierzą Leontieff'a w ujęciu finansowym). Jej elementy interpretujemy następująco:
"o ile wzrośnie produkcja finalna w dziale 'i' jeżeli produkcja globalna w dziale 'j' wzrośnie o 1 zł"
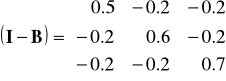
() Macierz (I-B)-1 nazywana jest macierzą współczynników materiałochłonności (lub dodatkowego zapotrzebowania) w ujęciu finansowym. Jej elementy interpretujemy następująco:
"o ile zł należy zwiększyć produkcję globalną w dziale 'i' aby produkcja finalna (końcowa) w dziale 'j' wzrosła o 1 zł"

( w przybliżeniu)
Układ równań bilansowych produkcji globalnej (Xj)
Bilans tworzenia produkcji globalnej (równanie kosztów)
Wartość produkcji = koszty materiałowe + płace + zyski
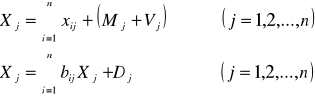
Warunek równowagi cząstkowej układu
Układ gospodarczy jest w równowadze cząstkowej jeżeli wartość produkcji liczone wg
bilansu podziału oraz
bilansu powstania
są sobie równe, tj.
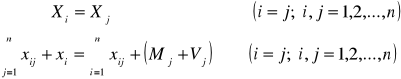
Warunek równowagi ogólnej układu
Układ gospodarczy jest w równowadze ogólnej jeżeli wartość dodana w układzie jest równa produkcji końcowej (finalnej) układu.
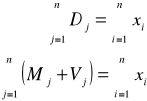
Warunek samowystarczalności układu
Układ gospodarczy nazywamy samowystarczalnym jeżeli dla każdego działu produkcja finalna (końcowa) jest nieujemna, tj.
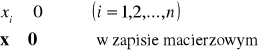
Wyznaczanie przyrostów produkcji globalnych i produkcji finalnych (końcowych)
Jeżeli zaplanowano przyrosty produkcji końcowych, to wymagane zmiany (przyrosty) produkcji globalnych można obliczyć, przy założeniu stałości powiązań międzygałeziowych, rozwiązując następujący układ równań
![]()
a w zapisie macierzowym ![]()
Na przykład
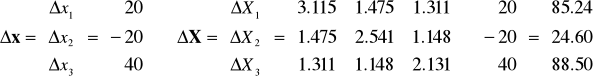
Jeżeli zaplanowano przyrosty produkcji globalnych, to zmiany w produkcjach finalnych (przyrosty) obliczyć, przy założeniu stałości powiązań międzygałeziowych, rozwiązując układ równań
![]()
Na przykład
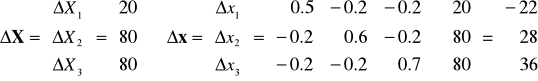
Tablica przepływów międzygałęziowych
(ujęcie ilościowe)
dział |
produkcja globalna |
przepływy międzygałęziowe [qij] |
produkcja finalna |
||
|
Qi |
qi1 |
qi2 |
qi3 |
qi |
1 [szt] |
80 |
40 |
20 |
12 |
8 |
2 [kg] |
50 |
8 |
20 |
6 |
16 |
3 [m3] |
60 |
16 |
20 |
18 |
6 |
Fudamentalnym pojęciem jest tutaj
współczynnik techniczny
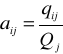
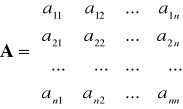
Interpretacja: ile jednostek produktu działu "i" musi być zaangażowane w wytworzenie jednostki produktu działu "j"
W przykładowym układzie 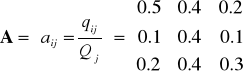
W ujęciu ilościowym rozważa się wyłącznie układ równań bilansowych produkcji globalnej (Qi)
Bilans podziału produkcji globalnej
wartość produkcji globalnej =
zużycie produkcyjne + produkcja finalna (końcowa)
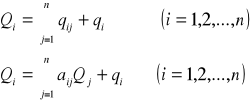
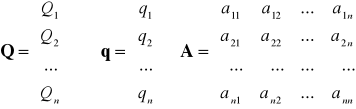
Układ równań bilansowych w zapisie macierzowym
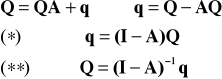
() Macierz (I-A) nazywana jest macierzą struktury technicznej. Jej elementy interpretujemy następująco:
"o ile jednostek wzrośnie produkcja finalna w dziale 'i' jeżeli produkcja globalna w dziale 'j' wzrośnie o jednostkę"
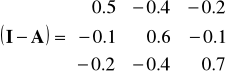
() Macierz (I-A)-1 nazywana jest macierzą współczynników materiałochłonności (lub dodatkowego zapotrzebowania) w ujęciu ilościowym. Jej elementy interpretujemy następująco:
"o ile jednostek należy zwiększyć produkcję globalną w dziale 'i' aby produkcja finalna (końcowa) w dziale 'j' wzrosła o jednostkę"

( w przybliżeniu)
Warunek samowystarczalności układu
Układ gospodarczy nazywamy samowystarczalnym jeżeli dla każdego działu produkcja finalna (końcowa) jest nieujemna, tj.
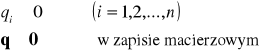
Wyznaczanie przyrostów produkcji globalnych i produkcji finalnych (końcowych)
Korzystamy tutaj z podobnego postępowania jak w ujęciu wartościowym stosując odpowiednio wzory
![]()
oraz ![]()
Równanie cen
Z równania kosztów mamy:
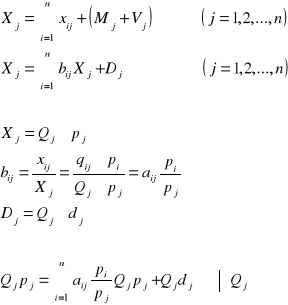
Układ równań cen ma postać:
![]()
Równanie cen - zapis macierzowy
![]()
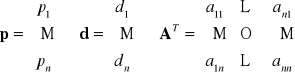
![]()
![]()
![]()
![]()
lewostr.
![]()
Wyznaczanie cen równowagi w układzie gospodarczym
Jeżeli dane są:
macierz współczynników technicznych A oraz
wektor jednostkowych wartości dodanych d (zyski+płace na jednostkę wyrobu),
to wektor cen równowagi wyznacza się z układu równań:
![]()
Przykładowo: jeżeli przyjmiemy, że wektor jednostkowych wartości dodanych (d) jest równy:
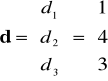
przy 
(liczby te mianowane są
w zł / jednostkę),
to wektor cen równowagi w układzie (p) będzie następujący

(liczby te mianowane są
w zł / jednostkę)
[11]
Wyszukiwarka