Jeżeli w kalorymetrze zachodzi jednocześnie kilka procesów o różnych efektach to oznaczona wielkość jest ich sumą:

Q = q₁ + q₂ + q₃ + …itd.

W celu wykonania ćwiczenia posłuży nam kalorymetr diatermiczny. Jest on używany do oznaczania ciepła reakcji chemicznych w fazie ciekłej. Osłonę zewnętrzną kalorymetru stanowi naczynie Dewara (termos), które ma na celu zmniejszyć wymianę ciepła między kalorymetrem a otoczeniem.

Sposób wykonania doświadczenia: W naczyniu Dewara umieszczam odmierzoną ilość wody (600 ml). W uchwycie umieszczamy szklaną ampułkę Nr 1 ze znaną ilością kwasu siarkowego( 5,89 g). Przykręcamy mieszadełko, które spowoduje, że temperatura cieczy wszędzie będzie taka sama. Umieszczamy sondę pomiarową w przeznaczonym na nią miejscu. Po zmontowaniu całego urządzenia wykonujemy 10 pomiarów co 30 sekund. Następnie tłuczemy ampułkę tak, aby kwas siarkowy zmieszał się z wodą. Kolejne 10 pomiarów odczytujemy co 10 sekund, a następne 10 co 30 sekund. Zmiany rezystancji termistora zapisuje w tabeli. W drugiej części ćwiczenia przygotowuję ampułkę szklaną z odważonym Na₂S₂O₃ (3,08 g) i topię ją w naczyniu z gotującą wodą. Następnie delikatnie schładzam pod zimną wodą. Tak przygotowaną ampułkę z przechłodzonym tiosiarczanem umieszczam w układzie kalorymetrycznym. Do naczynia Dewara wlewam znaną ilość wody (600ml). Odczytuje wskazania termistora co 30 sekund. Wrzucam do ampułki mały kryształek tiosiarczanu, aby zapoczątkować proces krzepnięcia. Odczytuje rezystancję co 10 sekund, a następnie co 30 sekund. Zmiany rezystancji zapisuje w tabeli

Część I

Oznaczanie pojemności cieplnej układu:

DANE:

• Waga ampułki Nr 1 pustej - 17,11 g

• Waga ampułki Nr 1 z reagentem - 23,00 g

• Masa - H₂SO₄ 23,00 - 17,11 =5,89 g

• Sonda pomarańczowo - niebieska -B=3814 [deg]

• R₂₅ = 14,24 [kΩ]

• Tabela rezystancji termistora R_T dla ampułki Nr1 oraz obliczonej temperatury środowiska.

Okres początkowy (co 30 sek)			Okres główny (co 10 sek)		Okres końcowy (co 30 sek)
Lp	[kΩ]	°C	[kΩ]	°C	[kΩ]	°C
1	40,00	2,80	38,00	3,82	37,60	4,04
2	40,00	2,80	36,87	4,43	37,77	3,95
3	40,00	2,80	36,86	4,44	37,87	3,89
4	40,00	2,80	36,89	4,42	37,95	3,85
5	40,00	2,80	36,95	4,39	38,07	3,79
6	40,00	2,80	37,01	4,36	38,21	3,71
7	39,90	2,85	37,10	4,31	38,22	3,71
8	39,90	2,85	37,20	4,25	38,23	3,70
9	39,90	2,85	37,29	4,20	38,25	3,69
10	39,90	2,85	37,40	4,14	38,26	3,69

Wykorzystując podane wartości stałych B i R₂₅ dla używanej sondy temperaturę środowiska obliczałam wg wzoru - T= B/(ln R_T - ln R₂₅ +B/ 298,15)-273,15

Przykładowo:

T=3814 / ( ln 40 - ln 14,29 +3814 / 298,15 )-273,15 = 2,80

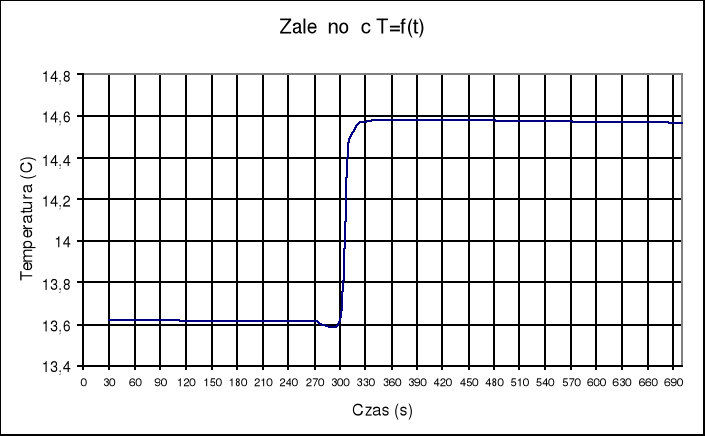
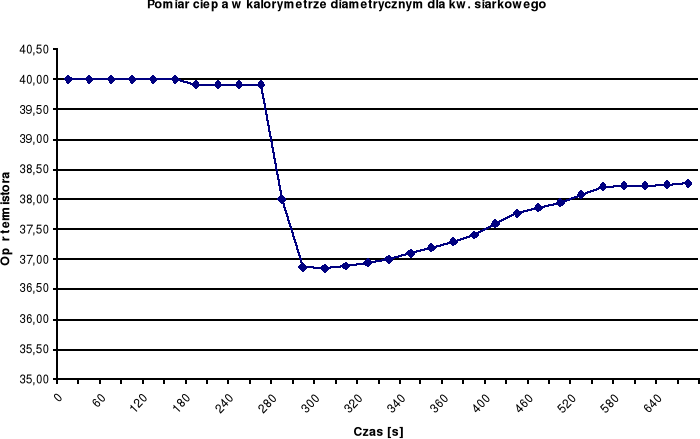
Na podstawie zanotowanych wskazań rezystancji termistora R_T wykonuję wykres w układzie osi R_T = f(czas)

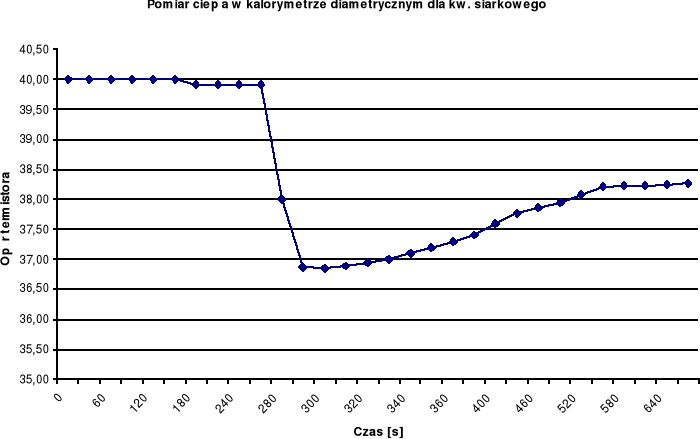
• Obliczam ilość moli wody:

1000 ml --- 55,5 mola wody

600 ml --- x

x = 33,3 mola wody

• Obliczam liczbę moli kwasu siarkowego
  

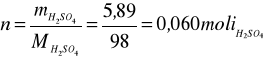
• Na 1 mol kwasu siarkowego przypada 555 moli wody. Znając molowe ciepła rozpuszczania kwasu w zależności od rozcieńczenia można określić ciepło jakie powstało w reakcji:

Q_rozp.≈ 76,80

• Wartość (Δt + ∑v) można wyznaczyć graficznie, ale tą sumę można wyliczyć z zależności:

(Δt + ∑v)= T_II - T_I

gdzie: T_I - końcowa temperatura okresu początkowego

T_II - początkowa temperatura okresu końcowego

(Δt + ∑v)= T_II - T_I = 4,04 - 2,85 = 1,19K

• Obliczam stałą pojemność cieplną kalorymetru ze wzoru:

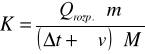
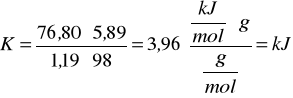
Część II

Pomiar ciepła krzepnięcia pięciowodnego tiosiarczanu:

DANE:

Masa Na₂S₂O₃ * 5H₂O =3,08 g

• Tabela rezystancji termistora dla ampułki ze stopionym tiosiarczanem

Okres początkowy (co 30 sek)			Okres główny (co 10 sek)		Okres końcowy (co 30 sek)
Lp	[kΩ]	°C	[kΩ]	°C	[kΩ]	°C
1	44,6	0,64	44,2	0,82	43,9	0,95
2	44,6	0,64	44,1	0,86	43,8	1,00
3	44,6	0,64	44,1	0,86	43,8	1,00
4	44,6	0,64	44	0,91	43,8	1,00
5	44,6	0,64	44	0,91	43,7	1,04
6	44,5	0,68	44	0,91	43,7	1,04
7	44,5	0,68	43,9	0,95	43,7	1,04
8	44,5	0,68	43,9	0,95	43,7	1,04
9	44,5	0,68	43,9	0,95	43,7	1,04
10	44,4	0,73	43,9	0,95	43,7	1,04

• Wyznaczam ilość ciepła mierzonego w procesie krzepnięcia:

(Δt + ∑v)= 0,4K

Q_mierz=3,96 *0,4 =1,58 kJ

• Obliczam liczbę moli tiosiarczanu:

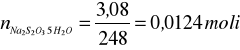
• Molowe ciepło procesu:

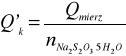
=127,42

• Obliczam molowe ciepło krzepnięcia zgodnie z równaniem Kirhoffa:

3. Wnioski

Proces zobojętniania mocnej zasady za pomocą mocnego kwasu jest w istocie relacją pomiędzy jonami H⁺ a OH^- z utworzeniem słabo zdysocjowanej cząsteczki wody:

H⁺ + OH^- → H₂O

Efekt cieplny tej reakcji wynosi około 13,7 kcal (57359). Wielkość ta praktycznie jest niezależna od rodzaju mocnej zasady i mocnego kwasu.

W ćwiczeniu został użyty słaby kwas, który w stanie równowagi pozostaje mieszaniną kwasu, jonów wodorowych oraz sprzężonej z tym kwasem zasady:

H₂SO₄ → 2H⁺ +SO₄^2-

Jeżeli w procesie zobojętniania zostanie użyta słaba zasada lub słaby kwas, to obserwowany efekt cieplny różni się znacznie od powyższej wartości, jaka jest podana dla mocnego kwasu i mocnej zasady. Wynika to stąd, że podczas zobojętniania słabego kwasu musi towarzyszyć proces dysocjacji tego kwasu.

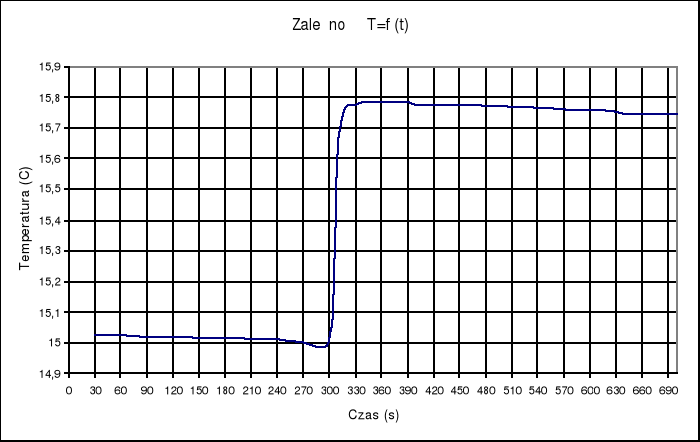
2. Ampułka z kwasem w roztworze wodorotlenku sodu:

---