nr ćw. 109	data 23.V	Krzysztof Kubicki	Wydział Elektryczny	Semestr II	grupa E-10
prowadzący mgr inż. Krzysztof Trybuś			przygotowanie	wykonanie	ocena końcowa

BADANIE RUCHU JEDNOSTAJNIE ZMIENNEGO.

Prędkość tego ciała możemy wyliczyć korzystając z prostej zależności:

=

gdzie:
- prędkość

Δt - czas

Δs - droga przebyta w czasie Δt

Tak zdefiniowaną prędkość nazywamy prędkością średnią.

Należy także wziąć pod uwagę przypadki gdy ciało porusza się ze zmienną prędkością. Wówczas należy wyliczać prędkość chwilową tego ciała, czyli prędkość jaką posiada to ciało w czasie Δt
0. Aby wyliczyć prędkość chwilową danego ciała należy skorzystać z następującej zależności:

v=

=

Widzimy więc, że prędkość chwilowa jest to pochodna drogi względem czasu.

Przyspieszenie.

Przyspieszeniem nazywamy przyrost prędkości w czasie wyrażający się wzorem:

=

Natomiast przyspieszeniem chwilowym nazywamy pochodną prędkości względem czasu i wyrażamy wzorem:

a=

Wiedząc, że prędkość chwilowa to pochodna drogi względem czasu możemy zdefiniować przyspieszenie jako drugą pochodną drogi względem czasu.

Równanie ruchu jednostajnie zmiennego.

Ruchem jednostajnie zmiennym nazywamy taki rodzaj ruchu, w którym przyspieszenie jest stałe.

Ruch jednostajnie zmienny możemy podzielić na ruch jednostajnie opóźniony, czyli taki w którym przyspieszenie jest stałe i mniejsze od zera, oraz ruch jednostajnie przyspieszony, czyli ruch jednostajnie zmienny, w którym przyspieszeni jest przybiera wartość dodatnią.

Poniżej znajdują się wzory stosowane przy obliczaniu wielkości charakteryzujących ten ruch.

Prędkość: v=v₀+at

Droga: s=v₀t+
at²

Przyspieszenie: a=const.

I. POMIAR PRZYSPIESZENIA ZIEMSKIEGO.

Lp.	Przyspieszenie ziemskie g	Błąd pomiaru
1	9,79	0,075
2	9,99	0,12
3	9,39	0,77
4	9,89	0,72
5	9,93	0,08
6	10,08	0,95
7	9,63	0,6
8	9,48	0,98
9	9,76	0,51
10	9,63	1,21

Wartość średnia
dla powyższych pomiarów :

, ostatecznie:

g=9,76
0,22

DYSKUSJA BŁĘDÓW :

Podczas wykonywania ćwiczenia zauważyłem, że drabinka nie zawsze w czasie lotu spadała pionowo. Zdarzało się, że przekrzywiała się co powodowało błędne wyniki. Możliwe jest także, że podczas upuszczania drabinki nadałem jej przyspieszenie, lecz jest to raczej mało prawdopodobne.

Porównując mój wynik g=9,76
0,22
, z tablicowym g=9,81
łatwo zauważyć, że jest on bardzo przybliżony.

2. BADANIE RUCHU JEDNOSTAJNIE ZMIENNEGO.

Lp.	m [kg]	m [kg]	m= m + m [kg]	m [kg]	[ ]	V=v +at
						a	v
1.	0,35	0	0,35	0,1	20	0,26	-0,2
2.	0,35	0,05	0,4	0,1	20	0,59	-0,4
3.	0,35	0,1	0,45	0,1	20	0,95	-1,07
4.	0,35	0,15	0,5	0,1	20	1,13	-1,32
5.	0,35	0,2	0,55	0,1	20	1,35	-1,17
6.	0,35	0	0,35	0,1	25	0,84	-0,44
7.	0,35	0,05	0,4	0,1	25	1,04	-0,08
8.	0,35	0,1	0,45	0,1	25	1,35	-1,65
9.	0,35	0,15	0,5	0,1	25	1,63	-1,6
10.	0,35	0,2	0,55	0,1	25	1,9	-2,27

Wyprowadzenia wzorów

- współczynnik tarcia kinetycznego

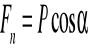
T=?

Dane mamy przyspieszenie. Pomijamy tarcie i poślizg nici o krążek oraz moment bezwładności krążka bo masa krążka jest dużo mniejsza od m
czy m.

- wypadkowa siła, która działa na wózek i m

- wypadkowa siła która działa na

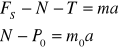
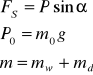
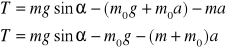
Obliczenia.

Lp.			[N]	[N]
1.	0,076	0,055	3,43	0,077	45,13	0,016
2.	0,065	0,066	2,94	0,088	45,23	0,023
3.	0,0056	0,077	2,45	0,099	43,75	0,031
4.	0,018	0,088	1,96	0,11	10,89	0,045
5.	0,014	0,099	1,47	0,12	10,5	0,068
6.	0,091	0,055	3,43	0,077	37,69	0,017
7.	0,157	0,066	2,94	0,088	18,73	0,024
8.	0,141	0,077	2,46	0,099	17,45	0,034
9.	0,113	0,088	1,96	0,11	17,36	0,048
10.	0,063	0,099	1,47	0,12	23,33	0,074

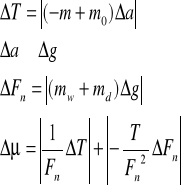
Po odrzuceniu najbardziej odbiegających wyników obliczyłem średnią arytmetyczną i odchylenie standardowe.

;

Wynik ostateczny:

WNIOSKI

W trakcie obliczeń zauważyłem spore różnice wyników. Po zastanowieniu się nad powodem wystąpienia błędów, znalazłem następujące powody ich występowania:

1. W obliczeniach zaniedbaliśmy ruch bloczka, tarcie nici o bloczek

2. Wózek nie poruszał się idealnie równolegle do krawędzi deski.

3. W trakcie ruchu wózka ciężarek wiszący na nitce wykonywał ruch wokół własnej osi, a także delikatny ruch wahadłowy.

---