Numer tematu: 6B
Temat: Analiza kinematyczna i kinetostatyczna mechanizmu suwakowego
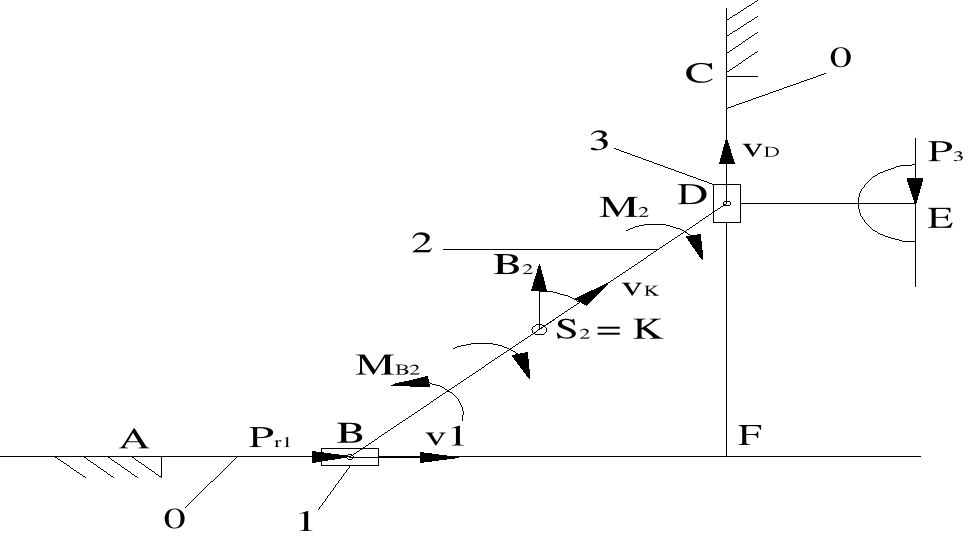
Zgodnie z numerem i wariantem liczbowym zadania przyjęto wymiary mechanizmu i położenie jak na rys. 1.
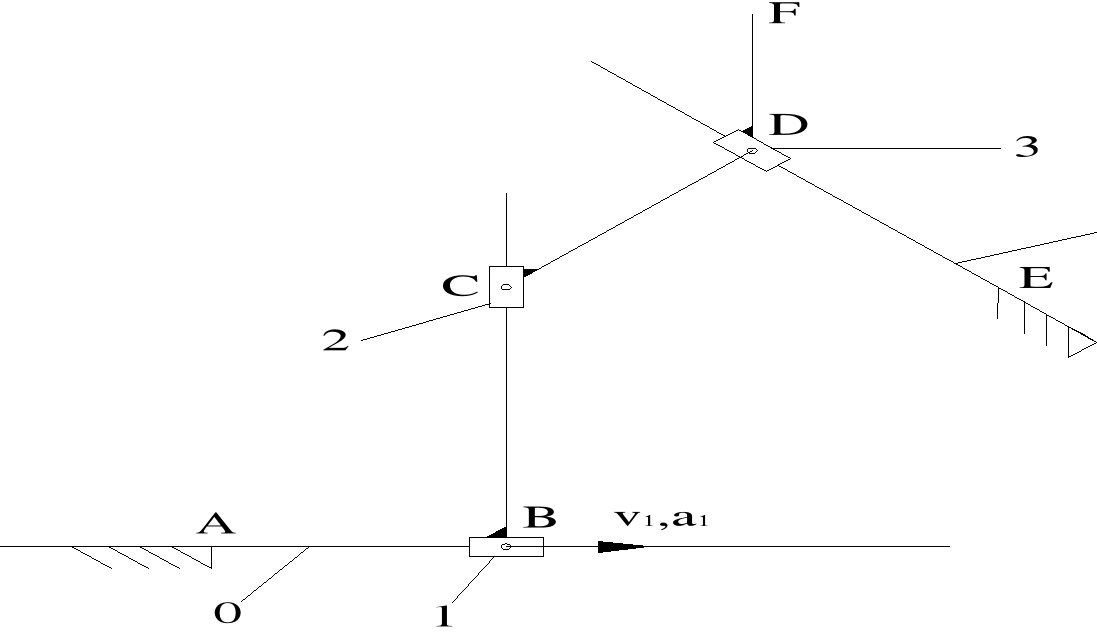
AB = 0,6 m
BC = 0,9 m v1 = 20 cm/s
CD = 0,707 m a1 = 20 cm/s
DE = 0,707 m
DF = 0,5 m
![]()
Analiza strukturalna mechanizmu - ruchliwość i klasa mechanizmu
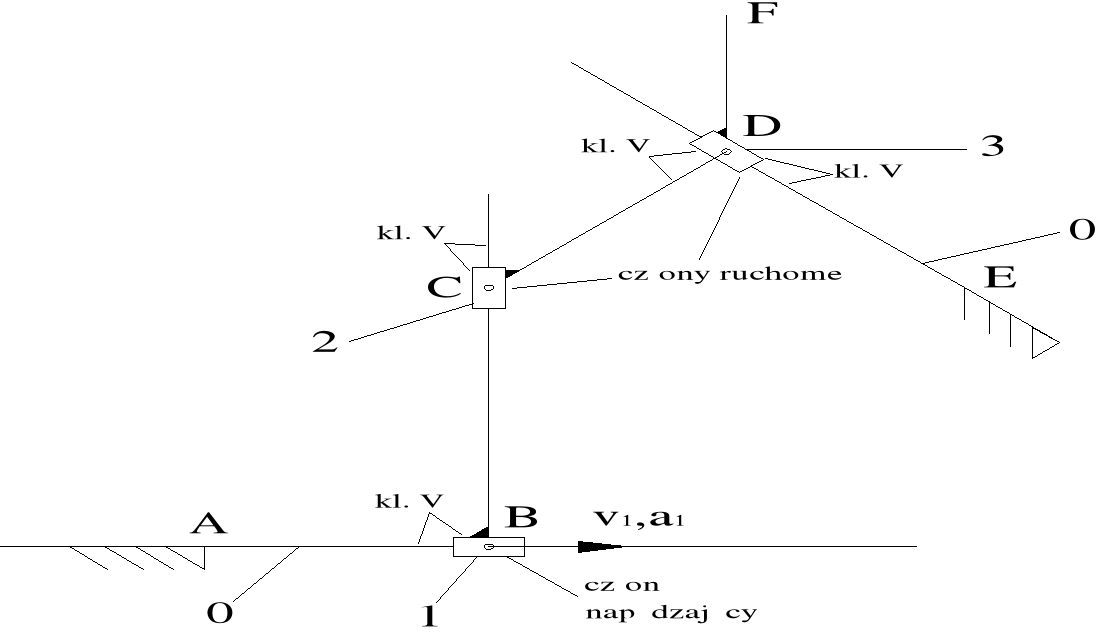
Ruchliwość mechanizmu:
w = 3⋅n - 2⋅p5 - p4
n = 3 p5 = 4 p4 = 0
w = 1
Podział mechanizmu na grupy strukturalne:
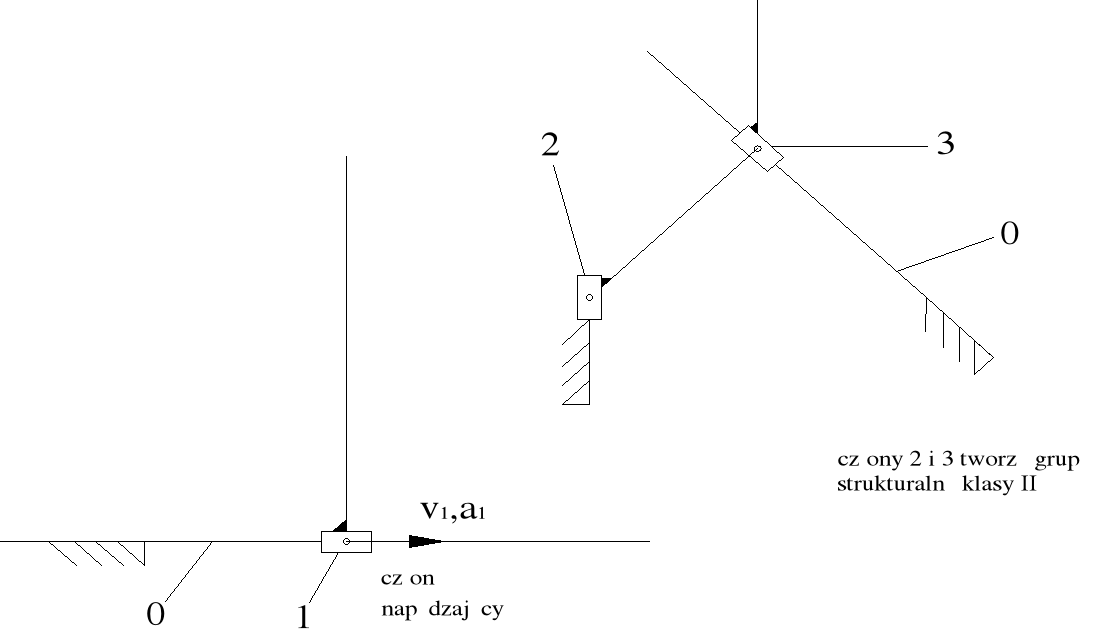
Analizowany mechanizm jest mechanizmem klasy II.
Analiza kinematyczna mechanizmu:
Metoda grafoanalityczna (metoda planów)
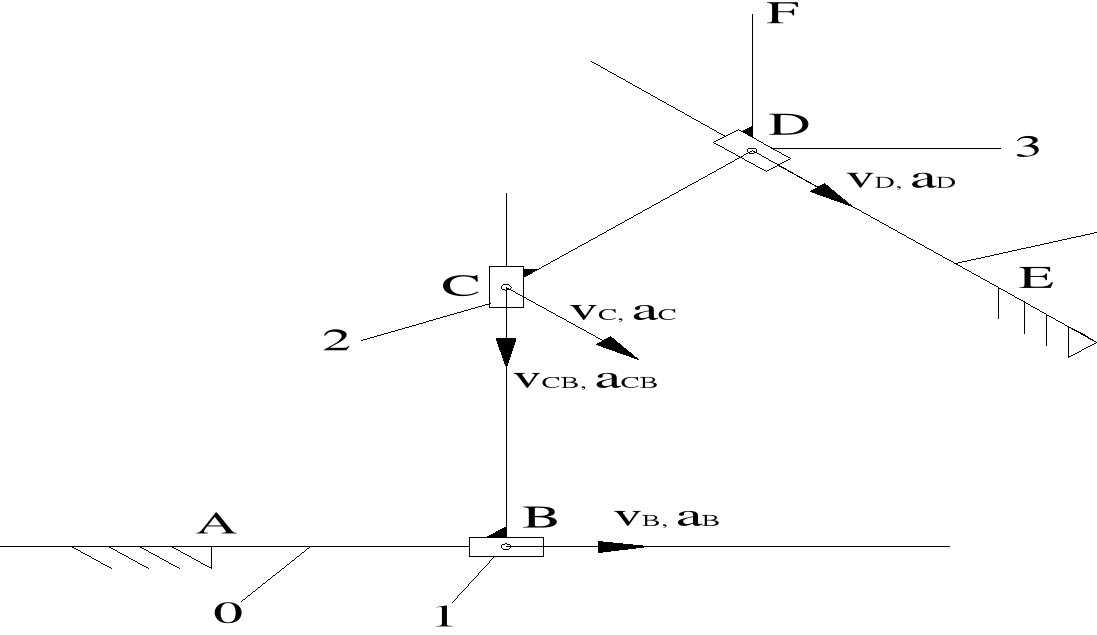
AB = 0,6 m
BC = 0,9 m vB = 20 cm/s
CD = 0,707 m aB = 20 cm/s
DE = 0,707 m
DF = 0,5 m
![]()
Analiza prędkości:
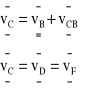
Analiza prędkości - plan prędkości:
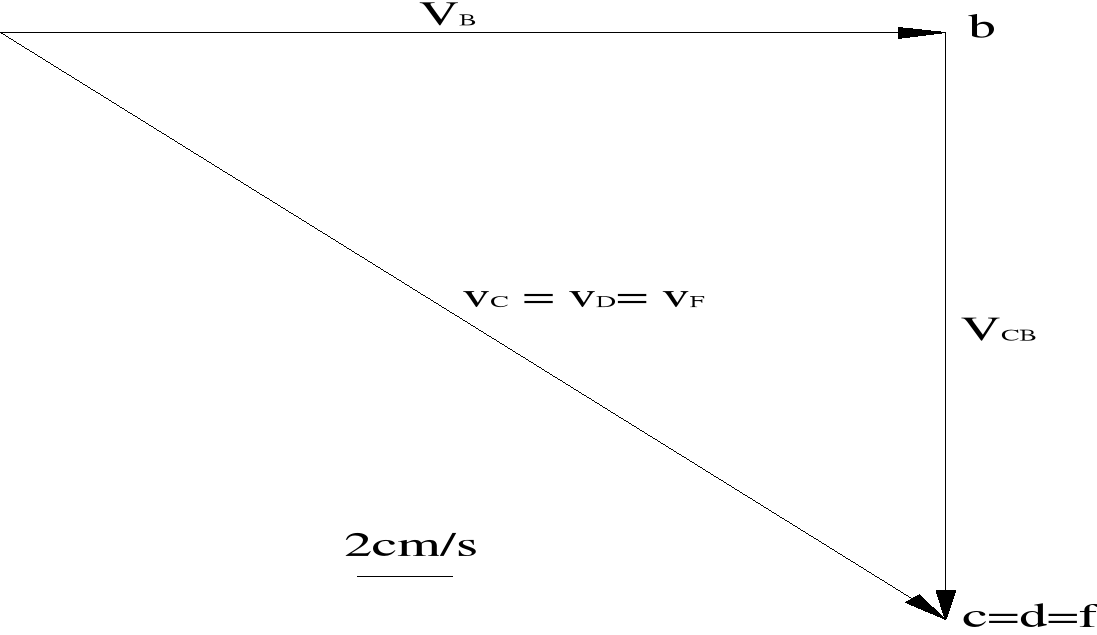
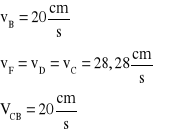
Na podstawie planu prędkości zaznaczono na rysunku zwroty prędkości ![]()
i ![]()
Analiza przyspieszeń:
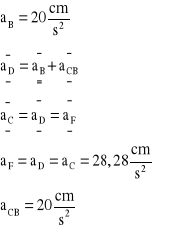
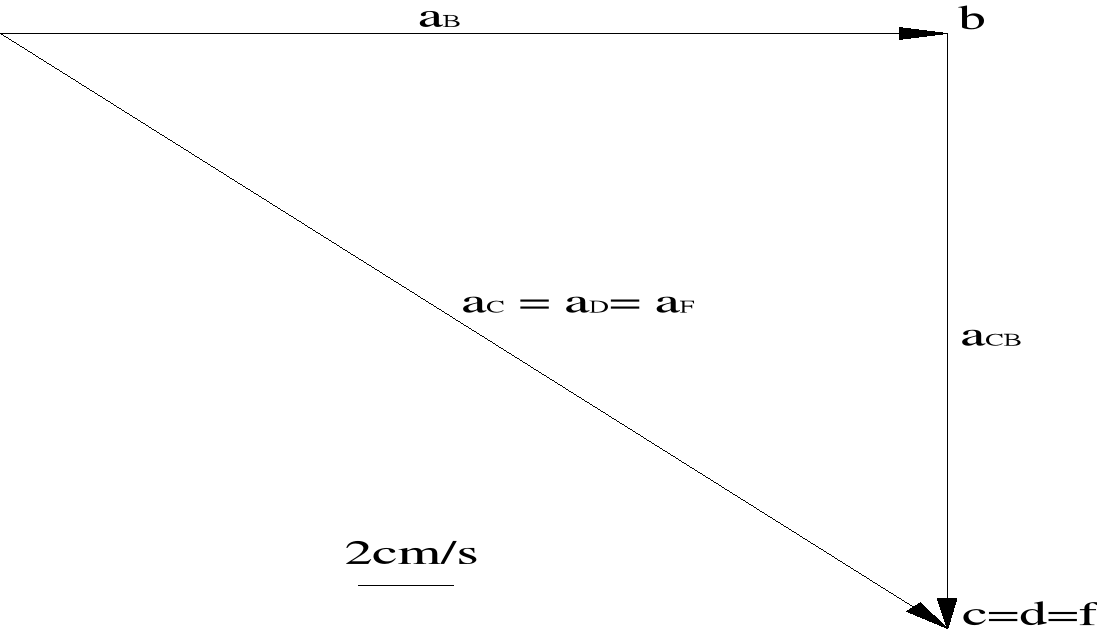
Na podstawie planu przyspieszeń zaznaczono na rysunku zwroty przyspieszeń ![]()
i ![]()
Analiza kinetostatyczna:
Przyjęcie mas, momentów bezwładności oraz sił oporu
m3 = 10 kg
Przyjmijmy siłę zewnętrzną P2 = 100N oraz P3 = 200N
Obliczanie sił i momentów od sił bezwładności:
![]()
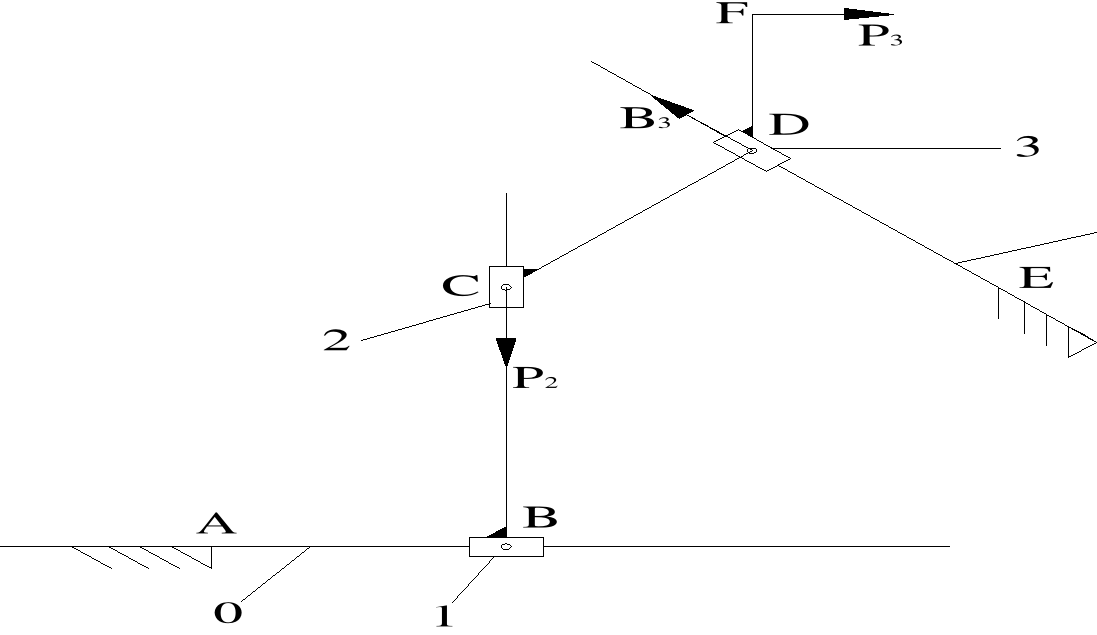
Oswobodzenie grupy strukturalnej od więzów:
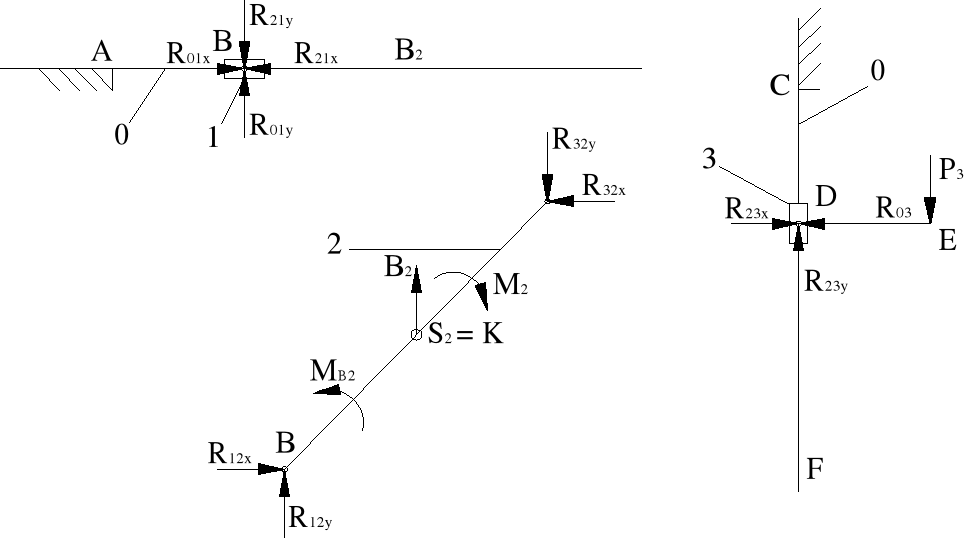
Równania równowagi sił zewnętrznych i reakcji:
R12x - R32x = 0
R12y + B2 - R32y = 0
MB2 + B2⋅0,5 - M2 - R32y⋅1 + R32x = 0
R32y = R23y = P = 100N
R12y = R21y = R32y - B2 = 100 - 0,04 = 99,96 N
R32x = M2 + R32y - 0,5⋅B2 - MB2 = 10 + 100 - 0,5⋅0,04 - 0,0066 = 109,97N
PR1 = R32x = 109,97N
Analiza kinetostatyczna - sprawdzenie poprawności obliczeń siły równoważącej metodą mocy chwilowych:
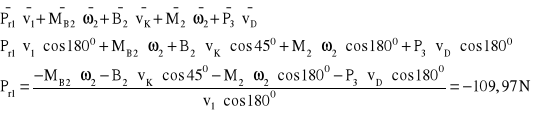
Wyszukiwarka