Numer ćwiczenia: 301	Data ćwiczenia: 26.04.2010	Imię i Nazwisko: Jakub Zmyslowski	Wydział: Technologii Chemicznej	Semestr II , Rok I Grupa 4
Prowadzący: Dr Mirosława Bertrandt	Przygotowanie i Wykonanie: Jakub Zmysłowski, Dawid Przybylski		Ocena:

„Wyznaczanie współczynnika załamania światła metodą najmniejszego odchylenia w pryzmacie”

Wprowadzenie.

Załamanie światła.

Promień światła napotykając na granicę pomiędzy dwoma ośrodkami tzn.przy przejściu z jednego ośrodka do drugiego ulega załamaniu (rys.1) . Kąt padania α , to kąt zawarty między prostopadłą do obydwu ośrodków a promieniem padającym P. Kąt załamania β , to kąt zawarty między prostopadłą N a promieniem przepuszczonym Z. Załamanie światła na powierzchni rozgraniczającej dwa ośrodki opisane jest prawem Snella.

Prawa Snella w postaci powyższej nie używa się do praktycznego wyznaczania współczynnika załamania ze względu na niedogodność i niedokładność wyznaczania kątów padania i załamania, natomiast możemy je skutecznie zastosować do pryzmatu, gdzie kąty α i β można wyrazić przez inne, dogodne do pomiaru wielkości.

W naszym ćwiczeniu wykorzystujemy tylko dwie płaszczyzny pryzmatu, tworzące między sobą kąt ϕ, zwany kątem łamiącym. Promień świetlny padający na pryzmat ulega dwukrotnemu załamaniu i zostaje odchylony o pewien kąt ϕ, zależny od kąta padania α oraz kąta od kąta łamiącego ϕ. Na podstawie rys. Możemy wyrazić kąt odchylenia następująco:

Kąt padania możemy tak dobrać, aby promień biegnący wewnątrz pryzmatu był prostopadły do dwusiecznej kąta łamiącego ϕ. W tej sytuacji bieg promienia jest symetryczny , tzn. α1=α2 oraz β1=β2, a kąt odchylenia - najmniejszy z możliwych dla danego pryzmatu. Biorąc ponadto pod uwagę , że 2β=ϕ , możemy przekształcić równanie do postaci:

Podstawiając wyrażone powyżej wartości α i β do wzoru definiującego współczynnik załamania, otrzymamy:

( 4 )

Stosując powyższy wzór możemy wyznaczyć n na podstawie pomiarów kąta łamiącego i kąta najmniejszego odchylenia.

Część praktyczna

Dane dodatkowe:

Nr filtra	3	4	5	6	7	8	9
λ [nm]	675	656	600	589	554	500	439

( tłustym drukiem zaznaczono filtry wykorzystane w ćwiczeniu)

Tabela wyników uzyskanych w doświadczeniu.

Nr filtra	α1 = 214.26° α2 [ ° ]
4	240.30
5	240.37
6	240.38
7	240.44
8	240.55

Obliczenia.

Do obliczenia wartości współczynnika załamania n wykorzystam wzór ( 4 )

1. Obliczam wartość kąta ϕ z równania:

otrzymuję: ϕ = (256.55° - 173.02°) / 2 = 44.765°

Tabela obliczeń kątów najmniejszych odchyleń δ_min i współczynnika załamania n.

Nr filtra	4	5	6	7	8
λ [ nm ]	656	600	589	554	500
[ ° ]	26.04	26.08	26.12	26.18	26.29
współczynnik załamania n (wzór 4)	1.528	1.522	1.523	1.524	1.526
błąd dn	0.033	0.033	0.032	0.033	0.032

Wzór na błąd pomiaru parametru n.

Błąd obliczony metodą różniczki:

błędy dδ i dϕ : dδ = 0.01° i dϕ = 0.01°

Wnioski:

Na podstawie otrzymanych wyników (dla strony Lewej) i wartości tablicowych możemy stwierdzić, że materiał z którego wykonany był pryzmat użyty w ćwiczeniu to szkło Crown lub szkło zwykłe.(wsp. zał. Światła w temp. 15°C dla filtra nr 6 {589 nm}wynosi dla szkła crown 1.525, dla szkła zwykłego 1.518) , w doświadczeniu otrzymałem 1.523±0.032.

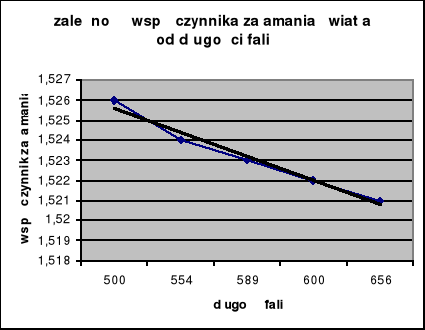
Prostokąty błędu na wykresie krzywej dyspersji n = f(λ) są tak duże, gdyż wynika to z przyjętej skali niemniej jednak wykres krzywej dyspersji przebiega prawidłowo tzn. im większa długość fali tym mniejsze złamanie.

--> [Author:MF]

1

---