6.Stacjonarność składnika losowego.
Odpowiedź na pytanie o stacjonarność składnika losowego jest jednocześnie weryfikacją założenia o stałości wariancji. Ponieważ stacjonarność rozumiemy jako brak istotnego związku szeregu reszt z czasem, zatem weryfikacja tego założenia, to odpowiedź na pytanie, czy miara takiego powiązania - współczynnik korelacji Pearsona różni się istotnie od zera.
Niech statystyka 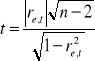
, gdzie 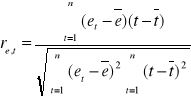
jest sprawdzianem hipotezy ![]()
składnik losowy jest stacjonarny} wobec hipotezy alternatywnej ![]()
składnik losowy nie jest stacjonarny}. Statystyka t ma rozkład t-Studenta o parametrach ![]()
. Z tablic rozkładu t-Studenta odczytujemy wartość krytyczną ![]()
. Jeśli ![]()
, nie ma podstaw do odrzucenia hipotezy ![]()
, jeśli natomiast ma miejsce relacja ![]()
, to należy odrzucić hipotezę ![]()
, i przyjąć hipotezę alternatywną ![]()
, co oznacza brak stacjonarności rozkładu składnika losowego.
W przypadku braku stacjonarności składnika losowego przyczyną może być niewłaściwa metoda estymacji. W takich przypadkach zalecana jest tzw. uogólniona metoda najmniejszych kwadratów. Metoda uogólniona różni się od klasycznej postacią funkcji kryterium dopasowania modelu do danych empirycznych, mianowicie:
![]()
,
gdzie ![]()
jest ilorazem wariancji składnika losowego w momencie czasu ![]()
do wariancji w momencie czasu ![]()
.
7. Weryfikacja założenia o wartości oczekiwanej składnika losowego.
Ten etap procedury weryfikacyjnej nie dotyczy modeli liniowych, bowiem metoda najmniejszych kwadratów daje gwarancje nieobciążoności składnika losowego, co wyraża się tym, że jego wartość oczekiwana jest równa zero. Weryfikację tej własności składnika losowego prowadzi się w przypadku modeli sprowadzalnych do postaci liniowej, modeli segmentowych, adaptacyjnych.
Weryfikacji poddajemy hipotezę ![]()
wobec hipotezy alternatywnej ![]()
. Sprawdzianem hipotez jest statystyka:
![]()
, gdzie S jest standardowym błędem oceny.
Statystyka t ma rozkład t-Studenta o (n-1) stopniach swobody. Z tablic rozkładu Studenta dla parametrów rozkładu ![]()
określamy wartość krytyczną statystyki ![]()
. Jeśli ![]()
nie ma podstaw do odrzucenia hipotezy ![]()
, jeśli natomiast ![]()
nie ma podstaw do przyjęcia hipotezy ![]()
, przyjmujemy hipotezę alternatywną ![]()
, co oznacza, iż ![]()
.
8. Autokorelacja składnika losowego
Analizując ciąg reszt uporządkowanych według wskaźnika czasu, można niekiedy zauważyć, że istnieje zależność reszt z okresu t od reszt przyporządkowanym okresom wcześniejszym. Zależność ta nosi nazwę autokorelacji. Literatura wyróżnia następujące przyczyny wystąpienia autokorelacji:
powolne wygasanie tendencji w kształtowaniu się wielkości ekonomicznych /bezwład/,
pominięcie istotnych zmiennych objaśniających,
przyjęcie błędnego założenia o postaci analitycznej,
pominięcie zmiennych opóźnionych w czasie,
błędy w ocenie opóźnień czasu niektórych zmiennych objaśniających,
„manipulowanie danymi” np. agregacja, bądź interpolacja brakujących informacji statystycznej.
W przypadku zależności pomiędzy szeregami opóźnionymi o jeden okres weryfikujemy hipotezę ![]()
wobec hipotezy alternatywnej ![]()
. Sprawdzianem jest statystyka:
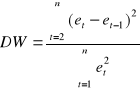
.
Przekształcając zdefiniowane wyrażenie otrzymamy:
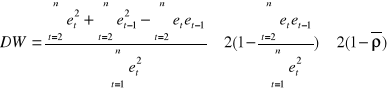
.
Z definicji współczynnik korelacji ![]()
należy przedziału [-1;1] tzn. /![]()
/, zatem statystyka DW należy do przedziału ![]()
.
Dla współczynnika korelacji z przedziału [-1,0), obserwujemy ujemną autokorelację, której z reguły odpowiada wartość DW z przedziału (2,4]. Natomiast dla autokorelacji dodatniej, współczynnik ![]()
należy do przedziału (0,1], a statystyka DW będzie się zawierała w przedziale [0,2].
W przypadku autokorelacja dodatniej, weryfikujemy hipotezę ![]()
wobec hipotezy alternatywnej ![]()
. Z tablic rozkładu statystyki Durbina - Watsona dla parametrów rozkładu (n,k) /k oznacza liczbę zmiennych objaśniających/ odczytujemy wartości ![]()
oraz ![]()
, są to wartości odpowiednio dolna oraz górna wartość krytyczna:
jeżeli
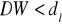
, hipotezę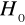
odrzucamy na rzecz hipotezy alternatywnej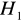
, oznacza to autokorelację składnika losowego,jeżeli
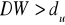
, nie mamy podstaw do odrzucenia hipotezy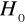
, oznacza to brak istotnej autokorelacji składnika losowego,jeżeli
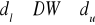
, nie mamy podstaw do przyjęcia bądź odrzucenia żadnej z dwu hipotez, jest to tzw. obszar niekonkluzywności testu Durbina - Watsona.
Jeśli ma miejsce przypadek autokorelacji ujemnej, korekcie poddajemy wartość statystyki DW, nowa wartość DW' jest różnicą 4-DW. Weryfikujemy hipotezę ![]()
, wobec hipotezy alternatywnej ![]()
:
jeżeli
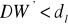
, hipotezę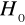
odrzucamy na rzecz hipotezy alternatywnej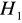
, oznacza to autokorelację składnika losowego,jeżeli
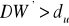
, nie mamy podstaw do odrzucenia hipotezy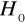
, oznacza to brak istotnej autokorelacji składnika losowego,jeżeli
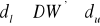
, nie mamy podstaw do przyjęcia bądź odrzucenia żadnej z dwu hipotez, jest to tzw. obszar niekonkluzywności testu Durbina - Watsona.
Oczywiście możliwe jest także łączne testowanie autokorelacji, bez rozstrzygania jej znaku.
Test Durbina - Watsona stosowany może być wówczas gdy w zbiorze zmiennych objaśniających modelu nie występuje opóźniona w czasie zmienna objaśniana. Jeżeli takie zmienne występują, wówczas w weryfikacji przyjętych hipotez korzystamy z testu - h, pochodzącego od Durbina:
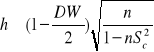
,
gdzie: ![]()
- ocena wariancji współczynnika regresji /parametr strukturalny/ przy ![]()
.
Test h ma jedno ograniczenie oczywiście poza tym, że weryfikuje autokorelację rzędu pierwszego, jest nim mianowicie to, że nie możemy wyznaczyć wartości h jeżeli ![]()
.
W przypadku autokorelacji rzędu p, w weryfikacji hipotezy o braku autokorelacji rzędu wyższego aniżeli jeden korzystamy z testu Godfreya.
Weryfikujemy hipotezę ![]()
autokorelacji rzędu p czyli ![]()
}, bowiem zakładamy, że w przypadku hipotezy alternatywnej składniki losowe są generowane przez proces autoregresyjny rzędu p, zapisujemy:
![]()
,
gdzie: ![]()
- składnik losowy o wartości oczekiwanej ![]()
, stałą wariancją ![]()
oraz zerowymi kowariancjami ![]()
dla ![]()
.
Hipoteza alternatywna wobec ![]()
przyjmie zatem postać:
![]()
miejsce autokorelacja rzędu i, tzn. istnieje takie i, że ![]()
Statystyka F ma rozkład Fishera - Snedecora z ![]()
stopniami swobody, gdzie ![]()
, a ![]()
, ![]()
oznacza liczbę szacowanych parametrów modelu.
Statystyka zaproponowana przez Godfreya jest równa:
![]()
,
gdzie:
![]()
,
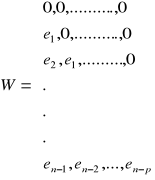
Test Godfreya ma dwa sprawdziany: ![]()
, dla dużych prób, oraz ![]()
o rozkładzie ![]()
dla małych prób. Pomiędzy sprawdzianami testu zachodzi relacja:
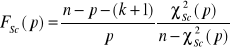
.
Jeżeli ![]()
lub ![]()
są większe od wartości krytycznych odczytanych z tablic rozkładu dla ustalonego poziomu istotności i właściwej liczby stopni swobody, nie ma powodów do przyjęcia hipotezy ![]()
, należy przyjąć hipotezę alternatywną ![]()
, co oznacza istnienie autokorelacji rzędu i. Jeśli zachodzi relacja przeciwna i obliczone statystyki ![]()
oraz ![]()
są mniejsze od wartości krytycznych odczytanych z tablic rozkładu, nie mamy podstaw do odrzucenia hipotezy ![]()
.
Wyszukiwarka