1. 
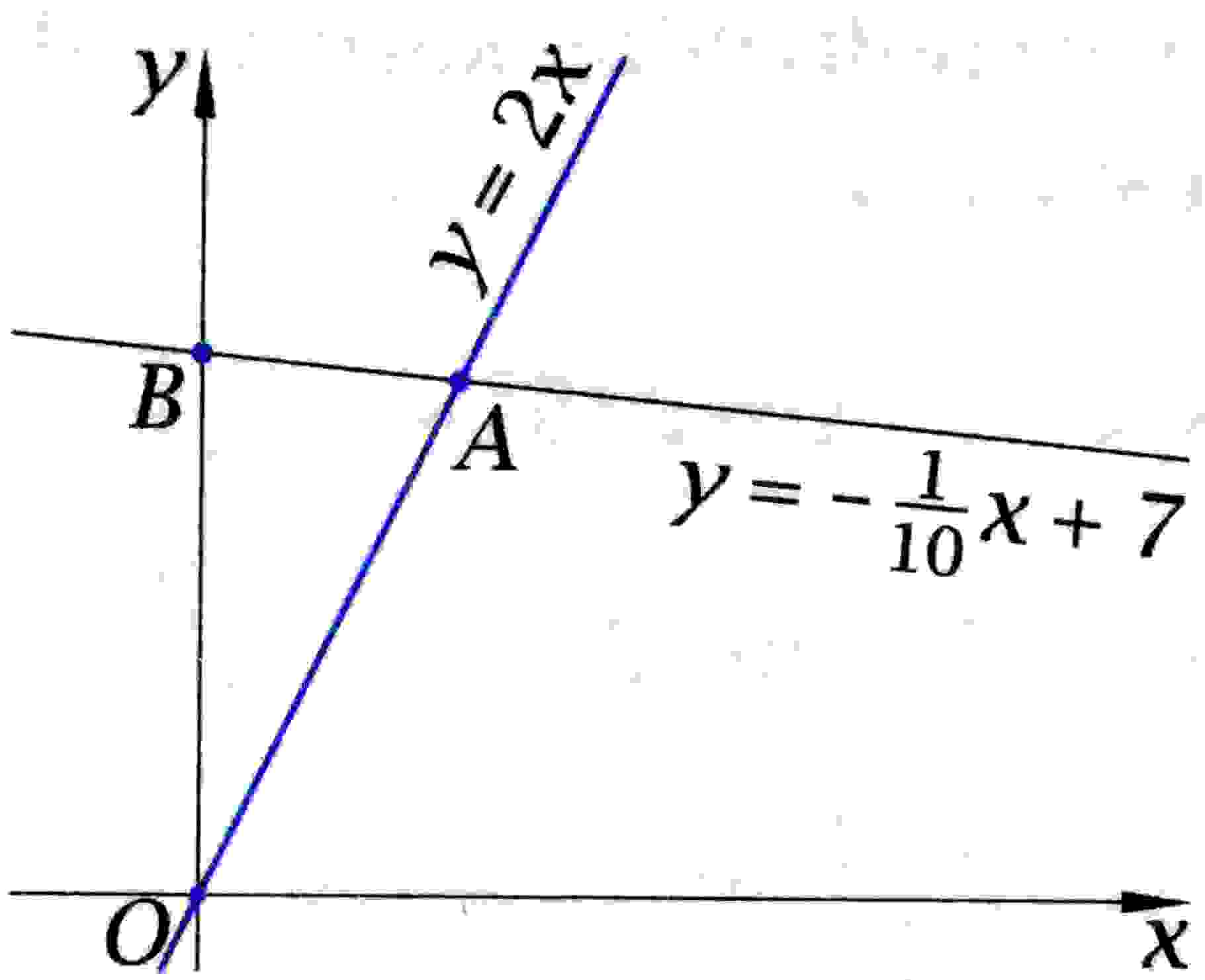
   Popatrz na rysunek obok a następnie:

1. Znajdź współrzędne punktów A i B

2. Oblicz pole trójkąta OAB

3. Oblicz sinus kąta OAB.

2. Punkty
   ;
   ;
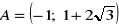
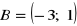
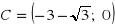
   są kolejnymi wierzchołkami równoległoboku ABCD. Oblicz współrzędne czwartego wierzchołka równoległoboku oraz miarę kąta ABC.

3. Podaj współrzędne wektora, który jest równoległy do prostej
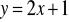
   i ma długość 1.

4. Dane są punkty A = (-4; 5), B = (1, 4) i C = (8, -4).

1. Jeden z tych punktów nie leży na prostej l o równaniu
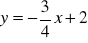
   . Oblicz odległość tego punktu od prostej l.

2. Oblicz pole trójkąta ABC

5. Dla jakich wartości
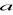
   prosta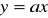
   ma przynajmniej jeden punkt wspólny z trójkątem o wierzchołkach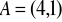
   ;
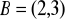
   i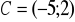
   .

6. Jakie współrzędne ma obraz punktu
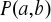
   w symetrii względem prostej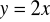
   ?

7. Punkt
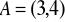
   jest wierzchołkiem równoległoboku, którego dwa boki zawarte są w prostych o równaniach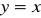
   i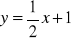
   . Znajdź współrzędne punktu przecięcia przekątnych oraz wysokość równoległoboku.

8. Przeczytaj poniższy tekst

1. Znajdź współrzędne kartezjańskie punktu C o współrzędnych biegunowych:
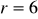
   oraz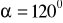
   

2. Znajdź współrzędne biegunowe punktu D o współrzędnych kartezjańskich
   ,
   

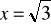
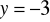
3. Naszkicuj dwa układy współrzędnych. W pierwszym zaznacz zbiór wszystkich punktów, których współrzędne biegunowe spełniają warunek
   (
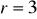
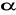
   jest dowolnym kątem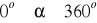
   ). W drugim układzie zaznacz zbiór wszystkich punktów, których współrzędne biegunowe spełniają warunek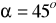
   .

9. Dwaj współudziałowcy chcą podnieść kapitał spółki, wykupując dodatkowe udziały, przy czym mają być spełnione dwa warunku:

1. zachowana jest zasada, że 88% udziałów m jeden udziałowiec i 12% drugi

2. każdy udział ma wysokość 500 PLN.

1. Ile udziałów powinien wykupić jeden, a ile drugi udziałowiec, aby kapitał został podwyższony o 100 tys. PLN?

2. Ile udziałów powinien wykupić jeden, a ile drugi udziałowiec, aby kapitał został podwyższony o co najmniej
   120 tys PLN?

10. Rozwiąż równanie
    

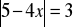
11. Rozwiąż nierówność
    

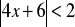
12. Znajdź liczby, które spełniają koniunkcję:
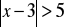
    i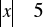
    

13. Hasło dostępu do komputera ma się składać z trzech cyfr i dwóch liter. Przyjmij, że na klawiaturze jest 25 liter oraz, że wielka i mała litera traktowane są jak dwa różne znaki.

1. Ile różnych haseł można ułożyć?

2. Ile jest haseł, które zaczynają się od litery A i nie zawierają cyfr parzystych.

14. Rozwiąż nierówność
    .

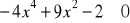
Zadanie egzaminacyjne - geometria analityczna - str.1