KOSZT KAPITAŁU W OCENIE PROJEKTU INWESTCJNEGO

Przedsiębiorstwa działające w gospodarce rynkowej muszą w swych decyzjach uwzględniać reguły panujące na rynku finansowym. To rynek finansowy poprzez swoje mechanizmy decyduje o alokacji kapitału i ryzyka w gospodarce oraz o koszcie kapitału pochodzącego z różnych źródeł.

We wzorach stosowanych do wyceny projektów inwestycyjnych koszt kapitału to jeden z kluczo­wych parametrów - im niższy jest koszt kapitału, tym wyższa efektywność projektów realizowanych przez spółkę.

Koszt kapitału przedsiębiorstwa obliczany jest jako koszt średni zdeterminowany strukturą kapitału i kosztem kapitału z poszczególnych źródeł. Struktura kapitału to efekt decyzji zarządu, natomiast koszt kapitału z poszczególnych źródeł zależy od stóp procentowych występujących na danym rynku oraz od oceny przedsiębiorstwa przez rynek. Koszt kapitału jest ściśle uzależniony od ponoszonego ryzyka, co z kolei oznacza, iż łatwiej będzie firmie znaleźć inwestora w przypadku, gdy firma jest stabilna i rozwojowa, a sytuacja gospodarcza w kraju, w którym firma działa, jest ustabilizowana i są optymistyczne rokowania, co do dalszego wzrostu gospodarczego. Wówczas ryzyko w tej inwestycji będzie mniejsze, w szczególności niskie jest ryzyko, gdy przedmiot inwestycji z góry zapewnia określony poziom stopy zwrotu z danej inwestycji.

Rozpatrując obiekt inwestycji, inwestor musi brać pod uwagę zasadę, iż wraz ze wzrostem oczekiwanej stopy zwrotu z inwestycji rośnie ryzyko. Stąd też uważa się za inwestycje praktycznie pozbawione ryzyka w ustabilizowanej gospodarce takie inwestycje, jak zakup obligacji skarbowych oraz lokaty bankowe w dużych bankach. Bardzo ryzykowną inwestycją są zakupy udziałów w spółkach, zwłaszcza od niedawna funkcjonujących.

Warunkiem realizacji czy to pojedynczego projektu inwestycyjnego, czy też całego programu rozwoju firmy jest zgromadzenie odpowiedniego kapitału. Możliwości inwestycyjne przedsiębiorstwa zależą w znacznej mierze od dostępności kapitału oraz od jego kosztów. Dlatego konieczne jest przede wszystkim określenie potencjalnych źródeł pozyskania kapitału inwestycyjnego.

Z uwagi na pochodzenie kapitałów źródła te dzieli się na:

• własne

• i obce.

Kapitał własny służący finansowaniu rozwoju przedsiębiorstwa może pochodzić z dwóch podstawowych źródeł:

• Z zysków zatrzymanych

• Z wkładów wnoszonych przez właścicieli poprzez objęcie nowych akcji lub udziałów.

Źródłem kapitału własnego może być pozyskiwanie dodatkowego kapitału od dotychczasowych bądź nowych właścicieli. W zależności od formy organizacyjno - prawnej sposób gromadzenia tego kapitału będzie różny.

W spółce akcyjnej podwyższenie kapitału własnego odbywa się drogą emisji i sprzedaży nowych akcji. Każda emisja akcji pociąga za sobą określone koszty, może również wiązać się z pewnym ryzykiem (czyli wzrost podaży akcji na giełdzie może spowodować spadek ich kursu i zmniejszyć wartość kapitału pozyskanego w drodze nowej emisji).

W spółce z ograniczoną odpowiedzialnością pozyskiwanie kapitału wiąże się w drodze sprzedaży udziałów wspólnikom (suma wszystkich udziałów odzwierciedla wartość kapitału zakładowego).

W spółkach osobowych kapitał pochodzi z wkładów właścicieli. W przypadku spółek już funkcjonujących kapitał ten może pochodzić zarówno z powiększenia wkładów przez dotychczasowych wspólników, jak i z poszerzenia grona współwłaścicieli wnoszących własne wkłady.

Kapitałem własnym jest kapitał pochodzący z zysków zatrzymanych i z emisji akcji zwykłych. Zgodnie z zasadą korzystania najpierw z najtańszego kapitału, przedsię­biorstwa emitują nowe akcje zwykłe po wykorzystaniu zysków zatrzymanych. Do szacowania kosztu kapitału własnego mogą być stosowane, w zależności od zakresu posiadanych informacji, różne modele.

Koszt kapitału własnego z zysków zatrzymanych

Wypracowany w przedsiębiorstwie zysk może zostać wypłacony właścicielom w formie dywidend (wypłat z zysku) lub reinwestowany. Przy szacowaniu kosztu kapitału pochodzącego z zysków zatrzymanych przyjmuje się, że właściciele firmy decydując o pozostawieniu zysku w celu jego reinwestycji w przedsiębiorstwie, oczekują minimum takiej stopy zwrotu jaką mogliby uzyskać nabywając za środki uzyskane dzięki wypłaconej dywidendzie akcje obarczone identycznym ryzykiem. Koszt kapitału z zysków zatrzymanych może być zatem wyliczony na podstawie oczekiwanej stopy zwrotu z akcji danej firmy.

Model CAPM

Model wyceny aktywów kapitałowych CAPM (capital asset prycing model), stara się odpowiedzieć na pytanie, jaki powinien być oczekiwany dochód z papierów wartościowych przy danym ryzyku.

k_e = r_f +ၢ_e * (r_m - r_f)

Gdzie:

• k_e - koszt kapitału własnego,

• r_f - stopa zwrotu z inwestycji wolnej od ryzyka ,

• ၢ _e - wskaźnik beta dla kapitału własnego firmy,

Współczynnik beta:

 

• β = 1 ryzyko przeciętne;

• β > 1 podwyższone ryzyko (im większa wartość β, tym większe ryzyko);

• β < 1 ryzyko stosunkowo niewysokie.

• r_m - stopa zwrotu z portfela rynkowego

Przykład modelu CAPM.

Przykład 1

Wolna od ryzyka stopa dochodu obligacji skarbowych wynosi r_f = 9%.

Współczynnik ryzyka rynkowego beta właściwy dla badanej spółki to β = 1,4.

Stopa dochodu dla akcji przeciętnych wynosi r_m = 14%.

Koszt zysku zatrzymanego spółki to:

k_e = 9% + 1,4 * (14% - 9%) = 9% +7% = 16%

 

Koszt kapitału (zysku zatrzymanego) na poziomie 16% oznacza, iż w przypadku, gdyby firma nie uzyskała stopy zwrotu z reinwestowanego zysku na poziomie wyższym niż 16%, należałoby rozważyć przeznaczenie tego zysku na dywidendę i wypłatę jej akcjonariuszom. W przeciwnym razie grozi spółce wyprzedaż akcji.

Przykład 2

Ustalono, że rozpatrywanemu projektowi można przypisać beta = 1,4 , a zatem jest to projekt wysoce ryzykowny. Wiadomo, że stopa procentowa wolna od ryzyka oraz rynkowa stopa procentowa są następujące: r_f = 8,0%, r_m = 10,2%. Oblicz koszt kapitału własnego, który ewen­tualnie zostanie wykorzystany przy realizacji projektu.

Korzystając ze wzoru otrzymujemy wynik:

 

k_e = 8,0 + (10,2 - 8,0) x 1,4 = 8,0 + 3,08 = 11,08%.

Taki sam rezultat powinniśmy otrzymać posługując się wielkościami ułamkowymi:

k_e = 0,08 + (0,102 - 0,08) x 1,4 = 0,08 + 0,0308 = 0,1108 = 11,08%.

W metodzie DCF do oszacowania kosztu kapitału własnego wykorzystuje się model wyceny akcji zwykłych. Jest to najprostszy i chyba najczęściej stosowany wariant modelu zdyskontowanych dywidend. Zakłada się w nim, że stopa wzrostu dywidendy jest i pozostanie stała na zawsze. Ma on następującą postać:

Gdzie:

• D₁ - dywidenda wypłacona w następnym roku,

• D₀ - dywidenda wypłacona w ostatnim roku;

• P_e - cena rynkowa akcji;

• g - tempo wzrostu dywidendy,

• k- wymagana stopa zwrotu

W powyższym modelu należy jeszcze przyjąć założenie, że r >g

Oprócz wymaganej stopy zwrotu wystarczy znać ostatnio wypłaconą dywidendę oraz stopę wzrostu dywidendy g. Jeśli chodzi o tę ostatnią wielkość, to często proponuje się zastosowanie następującego wzoru:

g = ROE - f

 

Gdzie:

• ROE - stopa zwrotu z kapitału własnego, określona na podstawie sprawozdania finansowego (Return On Equity);

• f - wskaźnik zatrzymania, określony jako iloraz zysku zatrzymanego i zysku netto.

Z wzoru Modelu Gordona wynika, że stopa zwrotu uzyskiwana przez obecnych akcjonariuszy wynosi:

• k_e - koszt kapitału własnego,

• D₀ - dywidenda wypłacona w ostatnim roku

• g - tempo wzrostu dywidendy,

• P_e - cena rynkowa akcji;

Model w takiej postaci stosowany jest do obliczania kosztu kapitału własnego pochodzącego z zysków zatrzymanych.

KOSZT KAPITAŁU OBCEGO

• Kapitał obcy cechuje się tym, że jest oddany do dyspozycji przedsiębiorstwa na czas określony, po terminie umowy musi być zwrócony. Korzystanie z niego związane jest z określonym kosztem - w postaci odsetek.

• Koszt kapitału obcego mierzy bieżący koszt firmy do zaciągania zobowiązań

i zależy od trzech składników:

• Stopy wolnej od ryzyka

• Ryzyka niewypłacalności przedsiębiorstwa (Default Risk),

• Korzyści wynikające z tarczy podatkowej.

 

• liczony wg nominalnej stopy oprocentowania długu z jakiego korzysta firma

• Program rozwoju przedsiębiorstwa może być również finansowany przy wykorzystaniu kapitału obcego (długu). Najczęstszym źródłem tego kapitału są:

• Długoterminowe i krótkoterminowe kredyty bankowe,

• Emisja obligacji zwykłych i zamiennych na akcje,

• Emisja krótkoterminowych papierów dłużnych,

• Leasing,

• Kredyt kupiecki od dostawców maszyn i urządzeń.

• Podejmując decyzje o sposobie finansowania projektów inwestycyjnych, przedsiębiorstwo musi brać pod uwagę nie tylko możliwości pozyskania kapitału. Konieczne jest również uwzględnienie kosztów kapitału oraz uwarunkowań związanych z kształtowaniem jego struktury. Wpływają one bowiem w sposób znaczący na efektywność przewidywanego do realizacji programu rozwoju firmy, a przez to kształtują zmiany jej wartości.

• Do wyliczenia kosztu kapitału obcego bierzemy stopę procentowa kredytu. Faktyczny koszt kredytu jest dla przedsiębiorstwa niższy niż jego oprocentowanie z uwagi na to, że koszty obsługi długu stanowią koszty uzyskania przychodu. Podatek płacony przez przedsiębiorstwo jest niższy niż iloczyn zapłaconych odsetek i stawki podatkowej. A zatem koszt kredytu to odsetki minus tarcza podatkowa:

K_e = K_n(1-T)

gdzie:

• K_e - (koszt kapitału obcego) efektywne oprocentowanie

• K_n - nominalne oprocentowanie

• T - stawka podatku dochodowego

PRZYKŁAD

• Przedsiębiorca zdecydował zaciągnąć kredyt oprocentowany 20% w skali roku. Zakładając, że firma płaci 28% podatek dochodowy, efektywny koszt kredytu wyniesie:

 

Odp:

• K_e = 20%(1-0,28) = 14,4%

Podobnie postępujemy w przepadku liczenia kosztu długu

• Efektywny koszt finansowania długiem uwzględnia korzyści z „osłony podatkowej” („tarczy podatkowej”). Odsetki płacone od zadłużenia są bowiem kosztem uzyskania przychodu, co pozwala na zmniejszenie wydatków na podatek dochodowy.

Warunek wykorzystania osłony podatkowej w pełnym zakresie: Zysk przed spłatą odsetek i opodatkowaniem musi być co najmniej równy kwocie odsetek.

 

r_D = i (1 - T)

• gdzie: r_D - koszt długu

• i - nominalna stopa procentowa

• T -stopa podatku dochodowego

Koszt obligacji

a) koszt kapitału ze sprzedaży obligacji

• gdzie:

• k_O -koszt kapitału ze sprzedaży obligacji

• O -wartość rocznych odsetek od obligacji

• T -stopa podatku dochodowego (wyrażona ułamkiem)

• V_O- skorygowana wartość rynkowa obligacji

B) skorygowana wartość rynkowa obligacji

• gdzie:

• V_O- skorygowana wartość rynkowa obligacji

• P_O- rynkowa cena obligacji

• m- liczba miesięcy, które upłynęły od ostatniej wypłaty odsetek

• i_O- oprocentowanie obligacji

Oczekiwana przez inwestorów stopa zwrotu z inwestycji w obligacje przedsiębiorstwa musi rekompensować wszystkie rodzaje ryzyka jakie związane są zakupem obligacji. Zakup obligacji dowolnego przedsiębiorstwa obarczony jest większym ryzykiem niż zakup obligacji Skarbu Państwa. Stąd stopa rentowności tych obligacji jest wyższa niż stopa rentowności oferowana prze obligacje Skarbu Państwa.

• 
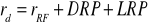
  Przedsiębiorstwo aby zachęcić inwestorów do nabycia obligacji musi zaoferować pewna premią w stosunku do stopy wolnej od ryzyka, którą oferują obligacje Skarbu Państwa. Premia ta odzwierciedla ryzyko niewypłacalności i ryzyko płynności. A zatem stopa oprocentowania obligacji korporacyjnych (przedsiębiorstw) zawiera następujące składniki:
  

• gdzie:
  rRF - stopa wolna od ryzyka,
  DRP - premia za ryzyko niewypłacalności,
  LRP - za ryzyko płynności.

• Przy ocenie opłacalności inwestycji używa się pojęcia stopy dyskontowej, czyli stopy procentowej, której dyskontuje się przepływy pieniężne.

• Stopa dyskontowa odzwierciedla oczekiwania inwestorów co do stopy zwrotu z zainwestowanego przez siebie kapitału.

R = RF + PR

• R - stopa dyskontowa,

• RF - (risk free rate) stopa wolna od ryzyka,

• PR - premia za ryzyko.

• Stopa wolna od ryzyka zależy od oprocentowania lokat bankowych, od oprocentowania obligacji skarbu państwa i bonów skarbowych. Jest to minimalna, oczekiwana stopa zwrotu przez inwestora.

• Premia za ryzyko zależy od kraju, w którym ma powstać inwestycja, od branży, od charakteru inwestycji i od samej firmy inwestującej (zarządzana profesjonalnie obarczona jest mniejszym ryzykiem).

ŚREDNI WAŻONY KOSZT KAPITAŁU

Koszt kapitału przedsiębiorstwa jest średnią ważoną kosztu poszczególnych składników kapitału. Wagami są udziały tych składników w kapitale służącym do finansowania działalności.

WACC = ၓ u _i * k _i

Gdzie:

• WACC - średnioważony koszt kapitału,

• u _i - udział i-tego źródła (składnika) kapitału w wartości kapitału ogółem

• k _i - koszt i-tego źródła (składnika) kapitału

• n - liczba źródeł (składników) kapitału

Koszt kapitału poszczególnych źródeł jest uzależniony od wymaganej stopy zwrotu, jakiej oczekują ich dostarczyciele. Wypłaty jakich dokonuje przedsiębiorstwo na rzecz swoich wierzycieli i właścicieli decydują o osiąganej przez nich stopie zwrotu z inwestycji. Dla firmy te wydatki są kosztem wykorzystania kapitału.

Przykład 3

Dana jest inwestycja o nakładach początkowych równych I_0 = 10.000 PLN. Koszt ten będzie sfinansowany z następujących źródeł:

 

Niepodzielone zyski 2.500 PLN

Kapitał akcyjny 6.000 PLN

Kredyt bankowy (dług) 1.500 PLN

----------

10.000 PLN

Zatem struktura finansowania prezentuje się następująco:

SKŁADNIK UDZIAŁ

 

Niepodzielone zyski 25%

Kapitał akcyjny 60%

Kredyt bankowy (dług) 15%

Jednocześnie koszty poszczególnych składników wynoszą (koszt po opodatkowaniu):

 

Niepodzielone zyski 15%

Kapitał akcyjny 25%

Kredyt bankowy (dług) 18%

 

Zgodnie ze wzorem, średni ważony koszt kapitału będzie się równał:

WACC = 0,25·0,15 + 0,60·0,25 + 0,15·0,18

WACC = 0,0375 + 0,1500 + 0,0270

WACC = 0,2145

Średni ważony koszt kapitału zaangażowanego w finansowanie tej inwestycji wynosi WACC = 21,45%.

Wcześniejszy wzór może przybierać następującą postać:

WACC = w _d k _d (1-T) + w _p k _p + w _e k _e

Gdzie:

w _d - udział kapitału obcego;

w _p - udział kapitału pochodzącego z akcji uprzywilejowanych;

w _c - udział kapitału własnego;

k_d - koszt kapitału obcego;

k - koszt kapitału pochodzącego z akcji uprzywilejowanych;

k_e - koszt kapitału własnego;

T - stopa podatku dochodowego płaconego przez spółkę.

Koszt kapitału obcego jest to koszt kredytu bankowego, gdy wierzycielem jest bank, lub stopa zwrotu, jakiej domagają się posiadacze obligacji wyemitowanych przez przedsiębiorstwo. Koszt kapitału obcego może być średnią ważoną, gdy przedsiębiorstwo korzysta z różnych kredytów bankowych i wyemitowało różne rodzaje obligacji. Koszt kapitału własnego zależy od tego, czy jest to kapitał własny wewnętrzny (pochodzący z zysków zatrzymanych), czy też zewnętrzny (pochodzący z emisji akcji zwykłych).

Miernik WACC jest przede wszystkim używany do:

a)dyskontowania przepływów pieniężnych planowanych do osiągnięcia z inwestycji podejmowanych przez przedsiębiorstwo (WACC jest stopą dyskontującą przyszłe przepływy pieniężne z inwestycji); jest on zatem jednym z kluczowym parametrów wykorzystywanych w metodologii oceny opłacalności projektów inwestycyjnych

b)dyskontowania przeciętnych dochodów przedsiębiorstwa i określania w ten sposób wartości podmiotu gospodarczego metodą dochodową zdyskontowanych przepływów pieniężnych

c)oceny wpływu struktury kapitału na wartość przedsiębiorstwa; bowiem im niższy jest średni ważony koszt kapitału, a więc lepiej jest dobrana struktura kapitałów finansujących działalność firmy, tym wyższa jest jej wartość; można zatem stwierdzić, iż WACC jest średnią oczekiwaną stopą zwrotu, której osiągnięcie jest konieczne do tego, aby cena akcji spółki nie pogorszyła się

d)wyznaczenia najniższej akceptowanej stopy zwrotu dla nowych przedsięwzięć inwestycyjnych przedsiębiorstwa; inwestycje generujące stopę zwrotu niższą od średnio ważonego kosztu kapitału je finansującego powinny być odrzucone.

Próg rentowności

• W zarządzaniu przedsiębiorstwem szczególnie ważna jest odpowiedź na pytanie:

Kiedy sprzedaż produktów zacznie przynosić zysk?

• Ponieważ koszty są kategorią pierwotną względem przychodów sprzedaż wyrobów do określonej wysokości nie przynosi zysku.

• Z punktu widzenia istnienia i rozwoju przedsiębiorstwa niezwykle ważne jest wyznaczenie minimalnej wielkości produkcji, której sprzedaż pozwoli zrównoważyć poniesione koszty.

• Analiz progu rentowności stanowi niezwykle pomocny instrument w zarządzaniu przedsiębiorstwem w gospodarce rynkowej. Obejmuje ona badanie tzw. Punktu wyrównania (break even point - BEP), w którym realizowane przychody ze sprzedaży pokrywają poniesione koszty. Przedsiębiorstwo nie osiąga wówczas zysku, ale też nie ponosi strat. Rentowność przychodów ze sprzedaży jest zerowa, co oznacza, że firma osiągnęła próg rentowności.

• Metoda analizy progu rentowności opiera się na podziale kosztów na stałe i zmienne.

W analizie progu rentowności przyjmujemy następujące założenia upraszczające:

• wielkość produkcji w badanym okresie jest dostosowana do wielkości sprzedaży (jest równa wielkości sprzedaży);

• koszty są funkcją wielkości produkcji;

• koszty stałe są jednakowe dla każdej wielkości produkcji;

• jednostkowe koszty zmienne są stałe i w związku z tym całkowite koszty zmienne zmieniają się proporcjonalnie do zmian wielkości produkcji;

• ceny sprzedaży poszczególnych produktów nie ulegają zmianie z upływem (czasu i nie zmieniają się również wraz ze zmianą skali produkcji i sprzedaży w całym badanym okresie; przychody ze sprzedaży są więc liniową funkcją ceny sprzedaży i ilości sprzedanych produktów;

• poziom jednostkowych kosztów zmiennych i kosztów stałych pozostaje niezmieniony w całym badanym okresie.

Próg rentowności przy produkcji jednoasortymentowej

Najpierw zbadamy próg rentowności przedsiębiorstwa wytwarzającego jeden produkt. Na poziom tego progu wpływają wówczas następujące czynniki:

• cena produktu,

• jednostkowe koszty zmienne,

• koszty stałe.

• Ilościowym (BEPil):

• wartościowym (BEPwart):

• procentowym (BEPproc)

Próg rentowności

• Próg rentowności w ujęciu ilościowym wyraża liczbę wyrobów jaką przedsiębiorstwo powinno sprzedać, aby pokryć koszty stałe i koszty zmienne.

• Próg rentowności znajduje się w punkcie, w którym wartość sprzedaży (Sr) jest równa poziomowi kosztów całkowitych,
  a więc:

Sr = Kc

Próg rentowności

Sr = BEPil x cj

Kc = Ks + BEPil x kzj

a zatem:

BEPil x cj = Ks + BEPil x kzj

BEPil x cj - BEPil x kzj = Ks

P ( cj - kzj ) = Ks

Ks

P = ------------ gdzie P = BEP

c - kzj

Ilościowy próg rentowności

• Ks - całkowite koszty stałe

• cj - cena jednostkowa

• Kzj - koszt zmienny jednostkowy

• Cj-kzj - marża jednostkowa na pokrycie

• BEPil - ilościowy próg rentowności

Wartościowy próg rentowności

• BEPil - ilościowy próg rentowności

• cj - cena jednostkowa

• BEP wart - próg rentowności w wyrażeniu wartościowym

Procentowy próg rentowności

• jako stopień zaspokojenia przewidywanego popytu (lub stopień wykorzystania zdolności produkcyjnej)

gdzie Pm - maksymalna możliwa wielkość sprzedaży określona na podstawie prognozy popytu (lub zdolności produkcyjnej).

Zadanie 1

Przedsiębiorstwo produkujące pralki ponosi w ciągu rozpatrywanego okresu koszty stałe w kwocie 50000 zł. Cena pralki wynosi 800 zł, a jednostkowy koszt zmienny 300 zł. Należy obliczyć próg rentowności ilościowy i wartościowy.

Ks = 50000

cj = 800

Kzj = 300

Cj-kzj = 800 - 300 = 500

BEPil = 10

BEPwart = 100* 800= 80000

Wykres progu rentowności

• Na podstawie równań przychodów ze sprzedaży oraz kosztów całkowitych możliwe jest również graficzne wyznaczenie progu rentowności (rysunek 1).

• Rysunek ten obrazuje ilościowy i wartościowy próg rentowności. Pozwala oni również ocenić, jaką część popytu (lub zdolności produkcyjnej) należy wykorzystać dla osiągnięcia progu rentowności. Porównanie krzywej przychodów ze sprzedaży i kosztów całkowitych umożliwia ponadto ustalenie przewidywanego poziomuj zysku, w zależności od zrealizowanej wielkości sprzedaży. Przy pełnym wykorzystaniu popytu (zdolności produkcyjnej) zysk ten wyniesie:

Zm - poziom zysku przy pełnym zaspokojeniu przewidywanego popytu (lub pełnym wykorzystaniu zdolności produkcyjnej).

Zm = Pm x c - (Ks + Pm x kz)

Próg rentowności - sporządzanie wykresu

• Aby sporządzić wykres należy dokonać podziału kosztów w okresie na koszty stałe i koszty zmienne.

• Sporządzić wykres jak na przykładowym rysunku poniżej, postępując w kolejności wskazanej na tym rysunku.

Próg rentowności - wykres

Uwagi:

A) W pierwszym kroku wykreślamy osie współrzędnych. Skala na nich powinna być jednakowa, aby wykres nadawał się do późniejszych symulacji.

B) Należy pamiętać, że oś pozioma nie ma nic wspólnego z czasem. Jest to oś oznaczająca wyłącznie SPRZEDAŻ OSIĄGNIĘTĄ W OKRESIE, np. w ciągu roku.

C) Sporządzając wykres najlepiej jest postępować według wskazanej na rysunku kolejności:

• Na osi poziomej oznaczyć sprzedaż osiągniętą w okresie, a następnie poprowadzić od nich pionową linię w górę.

• Na osi pionowej oznaczyć to samo (sprzedaż osiągniętą w okresie) i poprowadzić od nich poziomą linię (na rysunku cieniutka kropkowana) aż uzyska się punkt przecięcia z narysowaną poprzednio linią pionową. Przez ten punkt przecięcia i środek układu współrzędnych poprowadzić pomocniczą tzw. linię sprzedaży (na rysunku linia kreskowana). Dobrze jest upewnić się, że linia ta przebiega pod kątem 45 stopni do osi układu współrzędnych - wówczas wiadomo, że ten pierwszy etap sporządzania wykresu został zrealizowany prawidłowo.

• Wykreślić poziomą linię oznaczającą koszty stałe.

• Na linii pionowej do kosztów stałych dodać koszty zmienne. Od wyznaczonego w ten sposób punktu kosztów całkowitych poprowadzić tzw. linię kosztów zmiennych do punktu przecięcia linii kosztów stałych z pionową osią współrzędnych.

• Jeśli linia kosztów zmiennych przecina się z linią sprzedaży, punkt ich przecięcia wskazuje próg rentowności. Powyżej tego punktu przecięcia powstaje obszar, który na rysunku został zakreskowany.

D) Dokładną wartość progu rentowności możemy odczytać na osi poziomej. Próg rentowności jest to wielkość sprzedaży w okresie, która pokrywa koszty całkowite poniesione w okresie. Większa sprzedaż daje już zysk.

Zastosowania:

• Wyznaczanie wielkości sprzedaży docelowej dla potrzeb planowania.

• Symulacja skutków ekonomicznych programów, których celem jest redukcja kosztów i poprawa zyskowności przedsiębiorstwa.

• Obliczenie progu rentowności przedsiębiorstwa stwarza szerokie możliwości dalszej analizy. Obejmuje ona przede wszystkim oceną kształtowania się rentowności w przypadku zmian poszczególnych czynników wpływających na jej poziom.

Szczególne znaczenie ma przy tym zbadanie:

• jaki ewentualny spadek popytu na wytwarzane produkty może doprowadzić do całkowitej utraty rentowności przez przedsiębiorstwo,

jakie są możliwości zwiększenia zysku przedsiębiorstwa poprzez kształtowanie czynników określających jego poziom

• 
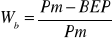
  Przedsiębiorstwo funkcjonujące w gospodarce rynkowej narażone jest na ciągłe niebezpieczeństwo spadku sprzedaży na skutek zmian warunków rynkowych. Celowe jest zatem ustalenie tzw. wskaźnika bezpieczeństwa, obrazującego wrażliwość przedsiębiorstwa na spadek popytu. Wskaźnik ten (Wb) obliczamy na podstawie:

• Jeżeli do osiągnięcia progu rentowności jest konieczne zaspokojenie pełnego popytu, to Wb = 0. Oznacza to, że już w chwili obecnej przedsiębiorstwo nie osiąga zysku. Każdy spadek popytu na wytwarzane produkty czy świadczone usługi przyniesie więc stratę. Z kolei im wyższy wskaźnik bezpieczeństwa (Wb 1), tym większy spadek popytu może przetrwać firma, nie ponosząc strat. Na przykład Wb = 0,5 oznacza, że nawet spadek popytu o 50% nie spowoduje strat, chociaż zredukuje zysk przedsiębiorstwa do zera.

• Ważna informacją dla bieżącego zarządzania przedsiębiorstwem jest również zbadanie potencjalnych możliwości podniesienia jego rentowności. Możliwości te tkwią zarówno po stronie przychodów ze sprzedaży, jak i po stronie kosztów.

Próg rentowności przy produkcji wieloasortymentowej

W praktyce gospodarczej przedsiębiorstwo produkuje lub dostarcza kila różnych usług. Analiza progu rentowności jest w tym przypadku utrudniona. Zaprezentowane dotychczas rozważania pozostają nadal aktualne. Lecz zachodzi konieczność uwzględnienia drugiego czynnika, jakim jest struktura asortymentowa sprzedaży. Podstawowe równania przyjmują wtedy postać:

• równanie wartości sprzedaży

• gdzie: S - wartość sprzedaży; Pi - liczba sprzedanych produktów i-tego asortymentu; ci - cena sprzedaży i-tego asortymentu; i = 1,…..,m - ilość wytwarzanych asortymentów produktów lub świadczonych usług.

równanie wartości sprzedaży

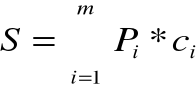
gdzie:

• S - wartość sprzedaży

• Pi - liczba sprzedanych produktów i-tego asortymentu

• ci - cena sprzedaży i-tego asortymentu

i = 1,…..,m - ilość wytwarzanych asortymentów produktów lub świadczonych usług

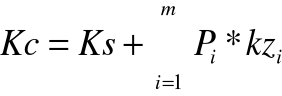
równanie kosztów całkowitych

• gdzie:

• Kc - koszty całkowite,

• Ks - koszty stałe,

• kzi - jednostkowe koszty zmienne

• i - tego asortymentu

• 
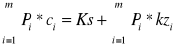
  Próg rentowności pokazuje, jaki poziom przychodów ze sprzedaży gwarantuje pokrycie poniesionych kosztów, a więc:

• O ile w przypadku produkcji jednorodnej próg rentowności był „punktem”, o tyle przy produkcji wielu wyrobów czy świadczeniu wielu usług jest on „zbiorem punktów”. Zrównoważenie przychodów ze sprzedaży i kosztów można, bowiem osiągnąć przy wielu różnych kombinacjach struktury asortymentowej. Próg rentowności można też osiągnąć na różnym poziomie wartościowym (z wyjątkiem szczególnych przypadków), zależnym od jednostkowego zysku realizowanego dla różnych punktów.

• Pewnym uproszczeniem dalszej analizy może być przyjęcie założenia, w myśl którego udział łącznych kosztów zmiennych (całej produkcji) w jej wartości jest stały i z góry określony. Wartościowy próg rentowności (BEPw') możemy wówczas ustalić na podstawie równania:

• O ile w przypadku produkcji jednorodnej próg rentowności był „punktem”, o tyle przy produkcji wielu wyrobów czy świadczeniu wielu usług jest on „zbiorem punktów”. Zrównoważenie przychodów ze sprzedaży i kosztów można, bowiem osiągnąć przy wielu różnych kombinacjach struktury asortymentowej. Próg rentowności można też osiągnąć na różnym poziomie wartościowym (z wyjątkiem szczególnych przypadków), zależnym od jednostkowego zysku realizowanego dla różnych punktów.

• 
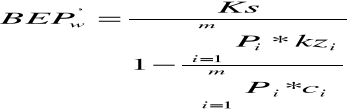
  Pewnym uproszczeniem dalszej analizy może być przyjęcie założenia, w myśl którego udział łącznych kosztów zmiennych (całej produkcji) w jej wartości jest stały i z góry określony. Wartościowy próg rentowności (BEPw') możemy wówczas ustalić na podstawie równania:

• 
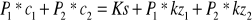
  Równie to służy głównie do oceny progu rentowności prowadzonej ex post. Znana jest wówczas rzeczywiście zrealizowana struktura asortymentowa sprzedaży, co umożliwia ustalenie udziału kosztów zmiennych w przychodach ze sprzedaży. Jednak wykorzystanie te relacji w analizie ex ante jest mało przydatne. Każda zmian struktury asortymentowej może bowiem zasadniczo zmienić poziom tej relacji.Najprostszym przykładem produkcji wieloasortymentowej jest wytwarzanie dwóch produktów. Równanie progu rentowności przyjmuje wówczas postać:

• 
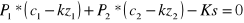
  gdzie: P1, P2 - wielkość sprzedaży produktów 1 i 2, c1, c2 - cena sprzedaży produktów 1 i 2. kz1, kz2 - jednostkowe koszty zmienne produktów 1 i 2, Ks - koszty stałe.

• Po odpowiednim przekształceniu wcześniejszej formuły uzyskamy następujące równanie:

Otrzymaliśmy równanie prostej. Rozwiązaniem tego równania będzie każdy punkt znajdujący się na tej prostej. Ponieważ badany przypadek dotyczy liczby wytwarzanych produktów, należy przyjąć założenie, że P1≥0 i P2≥0. Rozwiązaniem równania będzie wówczas jedynie odcinek. Analizując produkcję i sprzedaż określonych produktów, operujemy w zbiorze liczb naturalnych (powiększonych o 0). Jeżeli wielkość produkcji i sprzedaży wyrażamy w sztukach, ograniczymy zakres możliwych rozwiązań do skończonej liczby punktów leżących na tym odcinku.

• Marża brutto (marża na pokrycie) informuje o nadwyżce przychodów ze sprzedaży nad kosztami zmiennymi. Nadwyżka ta przeznaczana jest w pierwszej kolejności na pokrycie kosztów stałych, pozostała część - po przekroczeniu progu rentowności - jest zyskiem operacyjnym. Stopa marży brutto określa, jaka część przychodów pozostaje w dyspozycji po pokryciu kosztów zmiennych, na pokrycie kosztów stałych i pożądanego zysku. Stopę tę ustala się, korzystając ze wzoru

• 
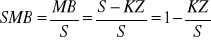
  gdzie MB - marża brutto.

• Próg rentowności zależy wprost proporcjonalnie od poziomu kosztów stałych i odwrotnie proporcjonalnie od wielkości stopy marży brutto. Zwiększenie kosztów stałych oraz udziału kosztów zmiennych w sprzedaży powoduje zatem, że przedsiębiorstwo przekracza później punkt krytyczny. Przyrost współczynnika udziału kosztów zmiennych w przychodach może być efektem spadku ceny oferowanych usług lub wzrostu kosztu zmiennego ich świadczenia. Wpływ analizowanych zmian na próg rentowności przedstawiono na rysunku 3 i 4.

• Z rysunku 3 wynika, że podwyższenie progu rentowności wskutek wzrostu kosztów stałych jest efektem równoległego przesunięcia w górę prostej kosztów całkowitych. Z kolei wzrost udziału kosztów zmiennych w przychodach ze sprzedaży prowadzi do podwyższenia punktu krytycznego na skutek zwiększenia kąta nachylenia prostej kosztów całkowitych.

Wzrost kosztów stałych i jego wpływ na próg rentowności

Wzrost udziału kosztów zmiennych w przychodach i jego wpływ na próg rentowności

• Zaprezentowana formuła progu rentowności pozwala na wyznaczenie minimalnej wielkości popytu zapewniającej dodatnią rentowność działalności przy danych kosztach uzyskania przychodów. Po odpowiednich przekształceniach możliwe jest także wyznaczenie granicznych wartości pozostałych parametrów, tzn. maksymalnego udziału kosztów zmiennych w przychodach i maksymalnego poziomu kosztów stałych przy danym poziomie sprzedaży. Wielkości te ustala się na podstawie wzorów:

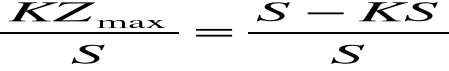
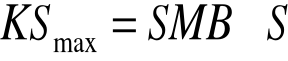
Analiza wrażliwości w ocenie projektów inwestycyjnych

Typowymi parametrami projektów inwestycyjnych są:

• nakłady inwestycyjne,

• poziom wykorzystania zdolności produkcyjnej,

• ceny sprzedaży produktów,

• koszty zakupu surowców,

• materiałów,

• płace,

• stopa oprocentowania kredytu,

• stopa dyskonta,

• okres życia projektu, itp.

• Budowa Planu finansowego

• Przeprowadzenie symulacji modelu planu finansowego wymaga zastosowania tylko jednej składowej

• Zbadanie wyników finansowych projektu

• Wyjaśnienie na czym polega analiza wrażliwości

Analiza wrażliwości ma na celu:

• ustalenie jak zmienią się wyniki finansowe projektu pod wpływem zmian wartości danych wejściowych

• ustalenie na zmiany których parametrów projekt wykazuje największą wrażliwość.

W analizie tej przeprowadza się kolejne symulacje modelu planu finansowego, wprowadzając za każdym razem zmienione wartości danego parametru.

Analiza wrażliwości może być przeprowadzona jako:

• badanie wpływu zmian jednego parametru

• badanie wpływu zmian kilku parametrów traktowanych oddzielnie

• badanie wpływu zmian kilku parametrów traktowanych łącznie

• badanie wpływu zmian cząstkowych danych wynikowych modelu.

• Przeprowadzenie analizy wrażliwości projektu pozwala w sposób pośredni ustalić ryzyko finansowe inwestycji..

• W praktyce analiza wrażliwości jest często stosowana wraz z analizą punktu krytycznego.

• Analiza wrażliwości w planowaniu procedury modelowania

W analizie wrażliwości jest modyfikowany jeden wskaźnik wejściowy. Istnieją dwa podstawowe podejścia do tego zagadnienia:

• można wykonać analizę wszystkich kluczowych wskaźników wejściowych zanim NPV osiągnie punkt obojętności

• alternatywnie można obliczyć określone zmiany w celu określenia wpływu na NPV.

• Przykład

Firma „X” inwestuje w pewne urządzenia100 000 zł. Ocenia się, że wygenerują one sprzedaż w wysokości 10 000 jednostek rocznie przez cztery lata. Marża jednostkowa jest spodziewana na poziomie 6 zł, koszt zmienny jednostkowy na poziomie 4, cena jednostkowa na poziomie 10. Koszty stałe na poziomie 46 000 zł. Koszt kapitału wynosi 5% , amortyzacja 20% a zysk w kolejnych latach wynosi 14 000zł.

W przykładzie mamy za zadanie:

1) obliczyć NPV,

2) wykazać jak może się zmienić każdy wskaźnik, zanim projekt stanie się dla przedsiębiorstwa obojętny?

DANE:

Rok	Sprzedaż (szt.)	Cena jednostkowa	Koszt zmienny (jedn.)	Marża jedn.	Koszt stały	Zysk
0	-	10	4	6	-	-
1	10 000	10	4	6	46 000	14 000
2	10 000	10	4	6	46 000	14 000
3	10 000	10	4	6	46 000	14 000
4	10 000	10	4	6	46 000	14 000

Przychody = 10 * 10 000 = 100 000

Koszty zmienne = 4 * 10 000 = 40 000

Marża na sprzedaż = 6 * 10 000 = 60 000

Amortyzacja

Amortyzacja roczna = 100 000 zł * 20%

Amortyzacja roczna = 20 000zł

Cash flow

CF = 14 000 + 20 000

CF = 34 000

Współczynnik dyskonta:

• dla roku „0” = 1/(1+0,05)^0 = 1

• dla roku „1” = 1/(1+0,05)^1 = 0,9523809527

• dla roku „2” = 1/(1+0,05)^2 = 0,9070294785

• dla roku „3” = 1/(1+0,05)^3 = 0,8638375985

• dla roku „4” = 1/(1+0,05)^4 = 0,8227024748

• PVn

• PV1 = 34 000 * 0,9524 = 32 380,9524

• PV2 = 34 000 * 0,9070 = 30 839,0023

• PV3 = 34 000 * 0,8638 = 29 370,4784

• PV4 = 34 000 * 0,8227 = 27 971,884

NPV

• NPV = - 100 000 + 120 562,32

• NPV = 20 562, 32

Inwestycja jest korzystna i możemy realizować projekt. NPV może się zmniejszyć o 20 562,32zł przed osiągnięciem punktu obojętności

Rok	Przychody	Koszty zmienne	Marża na sprzedaż	Zysk	Amorty- zacja	Roczny CF	CF Skumu- lowany	Dys- konto	Zdyskon-towane CF
0	-100 000					- 100 000	-100 000	1	-100 000
1	100 000	40 000	60 000	14 000	20 000	34 000	-66 000	0,95	32 380,95
2	100 000	40 000	60 000	14 000	20 000	34 000	-32 000	0,91	30 839,00
3	100 000	40 000	60 000	14 000	20 000	34 000	2 000	0,86	29 370,48
4	100 000	40 000	60 000	14 000	20 000	34 000	36 000	0,82	27 971,88
							SUMA	3,55

Oznacza to, że przepływy pieniężne mogą się zmienić o:

Przepływy pieniężne = 20 562,32 zł/3,546

Przepływy pieniężne = 5 800zł

• Koszty stałe mogą wzrosnąć do 5800 zł

• 5 800zł/46 000zł = 12,61%

• Jest to zmiana o 12,61%

• Wpływy mogą spaść o 5800 zł do 94 200 zł

• 100 000zł - 5 800zł = 94 200zł

• 5 800zł/100 000zł = 5,8%

• Jest to zmiana o 5,8%

• Zmiana spowodowana jest przez zmiany ceny i zmianę wydajności kosztowej

• Wielkość sprzedaży może spaść do 94 200 jednostek

• 94 200zł/10zł = 9 420 jednostki

• 10 000jednostki - 9 420jednostki = 580jednostek

• 580 jednostek/10 000jednostki = 5,8%

• Jest to zmiana o 5,8%

• Bez bardziej szczegółowej wiedzy o projekcie można prawdopodobnie założyć, że nie jest on wrażliwy na zmianę w kosztach stałych (ponieważ zmiana o 12,61 proc. wydaje się bardzo mało prawdopodobna).

• Analizowany projekt nie jest szczególnie wrażliwy na zmiany żadnego z obliczanych wskaźników. Z drugiej strony bardzo trudno jest przewidzieć przyszłe wielkości sprzedaży w niektórych projektach i można się spodziewać błędu w wysokości 10 proc. Wpływy składają się z wielu czynników (indywidualne koszty zmienne i cena sprzedaży) i bez dokładniejszej wiedzy nie jest możliwe wyciągnięcie dalszych wniosków.

Dla właściwej projekcji prawdopodobnej przyszłości można posłużyć się trzema wariantami:

• pesymistyczny

• prawdopodobny

• Optymistyczny

• Wycena spółki X na koniec 2007 roku

Dla ustalenia tych wariantów przyjęto następujące normy stosowane w krajach o gospodarce rynkowej:
- należności - 75-100% wartości księgowej,
- zapasy - 25-50% wartości księgowej,
- środki trwałe - 50-100% wartości księgowej,
- środki pieniężne - 100%.

		Wariant optymistyczny		Wariant najbardziej prawdopodobny		Wariant pesymistyczny
Wyszczegól- nienie	Wartość księg- owa	Współ-czynnik	Wartość likwida- cyjna	Współ-czynnik	Wartość likwida-cyjna	Współ-czynnik	Wartość likwida-cyjna
Środki trwałe	49,943	100%	49,943	75%	37,457	50%	24,972
Należności	67,746	100%	67,746	87,5%	59,278	75%	50,810
Zapasy	22,249	50%	11,125	37,5%	8,343	25%	5,562
Środki pieniężne	325,100	100%	325,100	100%	325,100	100%	325,100

• Analizę wrażliwości można przeprowadzić za pomocą arkusza kalkulacyjnego. Po zbudowaniu modelu można metodą prób i błędów zmieniać pojedynczą komórkę dla określenia zmiany potrzebnej do uzyskania zerowej wartości NPV.

• Ponieważ analiza wrażliwości jest przeprowadzana bez ustalania dokładnego prawdopodobieństwa wystąpienia określonego zdarzenia, jest łatwa do zastosowania.

A zatem użyteczność analizy tkwi w jej roli jako techniki zwracającej uwagę kierownictwa na czynniki, które mają największy wpływ na wyniki projektu. Uzbrojeni w taką wiedzę menedżerowie mogą podjąć kroki zmierzające do upewnienia się, że działania znajdujące się pod ich kontrolą pozostaną w ramach akceptowalnych parametrów. Ważne jest, aby nie interpretować błędnie wyników otrzymanych z analizy wrażliwości. Analiza ta stanowi spojrzenie na zmianę wartości czynnika w izolacji od innych uwarunkowań, a w rzeczywistym świecie prawdopodobne jest, że kilka czynników będzie się zmieniało razem tak, że rzeczywisty wynik projektu może zależeć od łącznych wyników kilku lub wszystkich zmiennych.

Analiza wrażliwości nie jest metodą, która umożliwia zmierzenie ryzyka, ani kryterium decyzyjnym. Jednak prawidłowo wykonana, pozwala na lepsze oszacowanie przyszłych wielkości i zmniejsza ryzyko projektu. Jest także przydatna w sytuacji, gdy porównujemy dwa zbliżone projekty inwestycyjne. Wtedy preferowane są projekty mniej wrażliwe na zmiany.

---