LABORATORIUM FIZYKI I |
Ćwiczenie nr 24 |
||||||
Wydział:
Inżynierii Chemicznej i Procesowej |
Dzień, godz.: Wtorek, 815-1100
|
Numer zespołu: 7 |
|||||
|
Data: 15.04.2008r.
|
|
|||||
Nazwiska i Imiona:
|
Ocena z przygotowania: |
Ocena ze sprawozdania: |
Ocena: |
||||
Prowadzący:
Dr Elżbieta Szerewicz |
Podpis prowadzącego: |
||||||
BADANIE EFEKTU HALLA
Podstawy teoretyczne.
Hallotron jest to cienka warstwa półprzewodnika naparowana na nieprzewodzące podłoże, zaopatrzona w 4 elektrody (długość warstwy naparowanej będziemy oznaczać przez l, a szerokość przez c).
Ruch nośników (elektronów i dziur) powoduje przepływ prądu sterującego IS . Na wszystkie nośniki działa jednakowa siła Lorentza skierowana prostopadle do kierunku ich ruchu oraz do wektora indukcji magnetycznej ![]()
.
![]()
Siła ta zakłóca ruch nośników powodując ich nagromadzenie na jednej z bocznych ścianek półprzewodnika aż do momentu wyrównania się siły Coulomba i siły Lorentza.
Skutkiem tego jest pojawienie się różnicy potencjałów pomiędzy powierzchniami bocznymi próbki, zwanej napięciem Halla (Uh).
Zjawisko to nazywamy efektem Halla. Wytwarzane przez te nośniki pole o natężeniu ![]()
działa na nie siłą ![]()
.
W stanie równowagi mamy:
![]()
Stąd otrzymujemy:
![]()
Prędkość dryftowa to prędkość jaką osiągają nośniki w próbce po przyłożeniu do niej napięcia.
Z powodu zderzeń z innymi nośnikami prędkość ta jest równa połowie prędkości między zderzeniami i jest wprost proporcjonalna do natężenia pola:
![]()
gdzie: μ - ruchliwość nośników prądu [![]()
].
Prędkość ta rośnie wraz ze wzrostem natężenia IS i maleje dla coraz większej koncentracji n cząstek, zgodnie ze wzorem:
![]()
gdzie: d - grubość płytki, n - koncentracja nośników, e - ładunek elementarny.
Ze wzoru na napięcie Halla otrzymujemy więc:
![]()
gdzie: ![]()
- spadek napięcia wzdłuż hallotronu.
Możemy wyznaczyć wzór na koncentrację nośników:
![]()
![]()
Cel ćwiczenia.
Celem ćwiczenia jest zapoznanie się ze zjawiskiem Halla oraz wyznaczenie koncentracji nośników.
Dane podstawowe.
Wymiary hallotronu:
- grubość: ![]()
,
- szerokość: ![]()
,
- długość: ![]()
.
Specyfikacja szczegółowa mierników:
Funkcja |
Zakres |
Klasa |
stałe napięcie DC |
200 mV |
± 0,5% rdg1) + 1dgt2) |
|
2 V |
|
prąd stały DC |
20 mA |
± 0,5% rdg1) + 1dgt2) |
1) rdg - wartość pomiaru 2) dgt - wartość ostatniej cyfry odczytu
Część I. Badanie asymetrii hallotronu.
Budujemy układ pomiarowy obwód elektryczny według schematu poniżej:
gdzie: E - źródło prądu, A - amperomierz, UH - woltomierz, H - hallotron, R - opornica dekadowa (Rmin = 0,1Ω).
Ta część ćwiczenia polegała na pomiarze napięcia i natężenia prądu dla hallotronu nieznajdującego się w polu magnetycznym. Pomierzone wartości zestawiono w tabeli.
Lp. |
IS [mA] |
Uh [mV] |
1 |
3,50 |
9,8 |
2 |
4,00 |
10,9 |
3 |
4,50 |
12,4 |
4 |
5,00 |
13,9 |
5 |
5,50 |
15,2 |
6 |
6,00 |
16,6 |
7 |
6,50 |
17,9 |
8 |
7,00 |
19,1 |
9 |
7,50 |
20,3 |
10 |
8,00 |
21,5 |
11 |
8,50 |
22,7 |
12 |
9,00 |
23,8 |
13 |
9,50 |
24,9 |
14 |
10,00 |
25,8 |
15 |
10,50 |
27,0 |
16 |
11,00 |
28,0 |
17 |
11,50 |
29,1 |
18 |
12,00 |
30,0 |
Zależności napięciowo-prądowe dla hallotronu nieznajdującego się w polu magnetycznym są wprost proporcjonalne do siebie, co wynika z asymetrii.
Część II. Badanie proporcjonalności napięcia Halla do natężenia prądu sterującego.
Modyfikujemy istniejący obwód elektryczny - w dotychczasowym układzie nic nie zmieniamy, dołączmy jedynie obwód z elektromagnesem (oraz miernikiem - amperomierzem), powodujący powstanie pola magnetycznego, które będziemy badać.
Następnie dokonujemy pomiarów napięcia dla tych samych wartości natężenia co w części I, kontrolując wskazanie amperomierza elektromagnesu - pożądana wartość to 1A (wtedy B = 0,130T oraz ΔB = 0,005T). Wyniki pomiarów przedstawiono w tabeli poniżej.
Lp. |
IS [mA] |
U [mV] |
1 |
3,50 |
62,6 |
2 |
4,00 |
71,5 |
3 |
4,50 |
80,5 |
4 |
5,00 |
89,4 |
5 |
5,50 |
98,2 |
6 |
6,00 |
107,0 |
7 |
6,50 |
115,8 |
8 |
7,00 |
124,2 |
9 |
7,50 |
132,6 |
10 |
8,00 |
141,0 |
11 |
8,50 |
149,8 |
12 |
9,00 |
158,0 |
13 |
9,50 |
166,5 |
14 |
10,00 |
174,5 |
15 |
10,50 |
182,5 |
16 |
11,00 |
190,2 |
17 |
11,50 |
198,0 |
18 |
12,00 |
206,0 |
Zależności napięciowo-prądowe dla hallotronu znajdującego się w polu magnetycznym, po odjęciu od wartości napięć Halla wartości napięć dla hallotronu w nieobecności pola magnetycznego przy tych samych natężeniach prądu, powinny być wprost proporcjonalne do siebie, co wynika z asymetrii hallotronu.
Opracowanie wyników pomiarów.
W tabeli poniżej wyliczone zostały niepewności wykonanych pomiarów, z uwzględnieniem zakresów woltomierza i amperomierza oraz `Szczegółowej specyfikacji mierników', przedstawionej na początku sprawozdania.
Zakres dla wszystkich wartości natężenia to 20mA, dla pomiarów napięcia od 1. do 17. zakres woltomierza to 200mV, a dla ostatniego, 18. pomiaru napięcia, 2V.
W tabeli znajdują się również wartości napięć hallotronu, znajdującego się w polu magnetycznym, po uwzględnieniu zjawiska asymetrii (Un), wyliczone z wzoru: Un = U - Uh.
Niepewności ΔUn wyliczone zostały ze wzoru ΔUn = ΔU + ΔUh (wzór ten można wyprowadzić, stosując metodę różniczki zupełnej dla wzoru na Un).
Lp. |
IS [mA] |
ΔIS [mA] |
Uh [mV] |
ΔUh [mV] |
U [mV] |
ΔU [mV] |
Un [mV] |
ΔUn [mV] |
1 |
3,50 |
0,02 |
9,8 |
0,8 |
62,6 |
0,9 |
52,8 |
1,8 |
2 |
4,00 |
0,02 |
10,9 |
1,0 |
71,5 |
0,9 |
60,6 |
1,8 |
3 |
4,50 |
0,02 |
12,4 |
0,5 |
80,5 |
0,9 |
68,1 |
1,4 |
4 |
5,00 |
0,03 |
13,9 |
1,0 |
89,4 |
0,8 |
75,5 |
1,8 |
5 |
5,50 |
0,03 |
15,2 |
0,3 |
98,2 |
0,7 |
83,0 |
1,0 |
6 |
6,00 |
0,03 |
16,6 |
0,7 |
107,0 |
0,5 |
90,4 |
1,2 |
7 |
6,50 |
0,03 |
17,9 |
1,0 |
115,8 |
1,4 |
97,9 |
2,4 |
8 |
7,00 |
0,04 |
19,1 |
0,2 |
124,2 |
0,8 |
105,1 |
1,0 |
9 |
7,50 |
0,04 |
20,3 |
0,4 |
132,6 |
1,3 |
112,3 |
1,7 |
10 |
8,00 |
0,04 |
21,5 |
0,6 |
141,0 |
0,7 |
119,5 |
1,3 |
11 |
8,50 |
0,04 |
22,7 |
0,8 |
149,8 |
1,5 |
127,1 |
2,4 |
12 |
9,00 |
0,05 |
23,8 |
0,9 |
158,0 |
0,8 |
134,2 |
1,7 |
13 |
9,50 |
0,05 |
24,9 |
0,9 |
166,5 |
1,3 |
141,7 |
2,3 |
14 |
10,00 |
0,05 |
25,8 |
0,9 |
174,5 |
1,4 |
148,7 |
2,3 |
15 |
10,50 |
0,05 |
27,0 |
0,1 |
182,5 |
1,4 |
155,5 |
1,5 |
16 |
11,00 |
0,06 |
28,0 |
0,1 |
190,2 |
1,2 |
162,2 |
1,3 |
17 |
11,50 |
0,06 |
29,1 |
0,2 |
198,0 |
1,0 |
168,9 |
1,2 |
18 |
12,00 |
0,06 |
30,0 |
0,2 |
206,0 |
1,0 |
176,0 |
1,2 |
By pokazać zależność liniową Un od IS należy wyznaczyć prostą: y = ax + b, obliczając współczynniki a i b, korzystając z metody najmniejszych kwadratów.
Owe współczynniki wyliczymy ze wzorów:
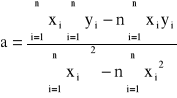
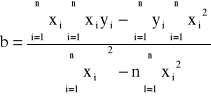
Za wartości x należy przyjąć IS, za y - Un.
Po obliczeniu otrzymujemy: a = 14,504 oraz b = 3,120.
Następnie wyliczamy średnie odchylenia standardowe współczynników:
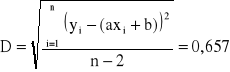

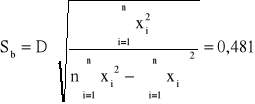
Zatem równanie szukanej prostej to: y = (14,504 ± 0,059)x + (3,120 ± 0,481)
Wykres badanej zależności napięcia Halla po uwzględnieniu asymetrii (Un) od natężenia prądu sterującego (IS) znajduje się w Załączniku 1 - Wykres Un = f(IS).
Na wykresie znajdują się punkty, dla których dokonano pomiarów wraz z wyliczonymi błędami.
Na wykresie tym narysowana jest również prosta, którą wyznaczono powyżej.
Wyznaczanie koncentracji nośników n.
By wyliczyć koncentrację nośników n należy skorzystać ze wzoru: ![]()
[![]()
].
Wzór ten należy jednak przekształcić do postaci: ![]()
, gdzie: a - wyznaczony wcześniej współczynnik kierunkowy prostej, e - ładunek elementarny elektronu, d - grubość hallotronu.
Takie przekształcenie jest możliwe, ponieważ: ![]()
tak, że: ![]()
[![]()
].
Dane do podstawienia:
![]()
![]()
![]()
![]()
Zatem: 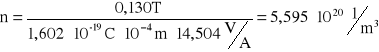
.
By policzyć niepewność otrzymanego wyniku korzystamy z metody różniczki logarytmicznej.
Po zlogarytmowaniu wzoru na n i usunięciu stałych, otrzymujemy wzór:
![]()
,
który po przekształceniu staje się wzorem na błąd wyliczonej koncentracji nośników:
![]()
,
gdzie za ![]()
należy wstawić wyliczone wcześniej odchylenie Sa.
Podstawiając do powyższego wzoru odpowiednie wartości otrzymujemy więc:
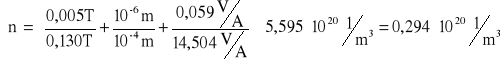
Ostateczny wynik koncentracji nośników wynosi więc: ![]()
.
Wnioski.
W doświadczeniu wykazaliśmy, że zależność napięcia Halla od natężenia prądu sterującego jest rzeczywiście zależnością liniową (ilustruje to załączony wykres).
Napięcie Halla jest więc wprost proporcjonalne do natężenia prądu sterującego.
Liniową zależność wykazuje również napięcie zmierzone dla hallotronu nieznajdującego się w polu magnetycznym, co wynika z asymetrii.
Wyliczyliśmy również koncentrację nośników prądu. W naszych obliczeniach założyliśmy, że występują jedynie nośniki jednego znaku.
Strona 1 z 7
Wyszukiwarka