Identyfikacja i estymacja wielorównaniowych liniowych modeli ekonometrycznych
Identyfikacja modeli wielorównaniowych
Wspomniano już, że estymacji parametrów modelu wielorównaniowego dokonuje się dla postaci zredukowanej
![]()
.
Postać ta nie odzwierciedla, w przeciwieństwie do postaci strukturalnej, ekonomicznej treści zależności między zmiennymi. Dlatego pożądana jest możliwość powrotu do postaci strukturalnej
Proces przekształcania postaci zredukowanej modelu do postaci strukturalnej nazywa się identyfikacją modelu, a możliwość jej przeprowadzenia dla modelu (lub poszczególnych jego równań) określa własność identyfikowalności modelu (lub równania). Określenie identyfikowalności modelu powinno poprzedzić proces estymacji parametrów.
Równanie postaci strukturalnej modelu nazywamy identyfikowalnym, jeżeli jest możliwe wyznaczenie (niekoniecznie jednoznaczne) wartości parametrów tego równania na podstawie znajomości parametrów postaci zredukowanej modelu. Model jest identyfikowalny, jeżeli wszystkie jego równania są identyfikowalne. W przeciwnym razie o równaniu lub modelu mówimy, że są nieidentyfikowalne.
Model (lub równanie) jest jednoznacznie identyfikowalny, jeżeli przekształcenie postaci zredukowanej w strukturalną jest jednoznaczne. W przeciwnym przypadku model jest niejednoznacznie (lub nadmiernie) identyfikowalny.
Przykład
Weźmy omawiany wcześniej model produkcji
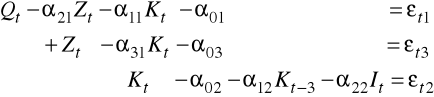
w postaci zredukowanej mamy
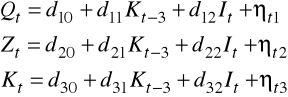
.
gdzie
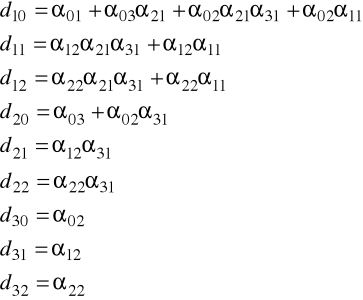
W postaci strukturalnej występuje 8 nieznanych wartości parametrów ![]()
, w postaci zredukowanej zaś 9 wartości dij. Zauważmy, że gdybyśmy znali wartości parametrów postaci zredukowanej, z ostatnich trzech zależności wyznaczymy automatycznie wartości parametrów trzeciego równania strukturalnego ![]()
. Następnie z kolejnych (od końca) dwóch zależności byłoby można wyznaczyć na dwa sposoby
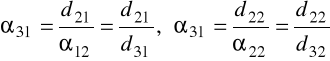
(oczywiście o ile d31 oraz d32 są różne od zera).
Z kolejnego równania moglibyśmy dalej wyznaczyć ![]()
i podstawiając do kolejnych dwóch równań wyznaczone już wartości otrzymać ![]()
i ![]()
, a podstawiając wszystkie znane parametry do zależności pierwszej wyznaczyć z niej ![]()
. Jednak aby otrzymać jednoznaczne wartości parametrów postaci strukturalnej, musiałby być spełniony warunek 
. W przeciwnym razie otrzymujemy sprzeczność. Bez spełnienia powyższego warunku jedynym równaniem, dla którego potrafimy znaleźć jednoznaczne wartości parametrów jest równanie drugie postaci strukturalnej. Zatem model jest niejednoznacznie identyfikowalny, zaś drugie równanie postaci strukturalnej jest jednoznacznie identyfikowalne.
Warunki identyfikowalności modeli
Model wielorównaniowy jest nieidentyfikowalny, jeżeli liczba nieznanych parametrów w macierzach A i B postaci strukturalnej jest większa niż liczba równań otrzymana z równania macierzowego:
![]()
.
Modele proste są zawsze jednoznacznie identyfikowalne.
Modele rekurencyjne zawsze są identyfikowalne, choć nie musi to być identyfikowalność jednoznaczna (co było widać w ostatnim przykładzie).
Modele o równaniach łącznie współzależnych mogą być zarówno jednoznacznie lub niejednoznacznie identyfikowalne, jak i nieidentyfikowalne.
Warunkiem koniecznym identyfikowalności i-tego równania w modelu o równaniach łącznie współzależnych jest, aby liczba zmiennych endogenicznych nieopóźnionych występujących w tym równaniu gi pomniejszona o jeden była niewiększa od liczby zmiennych z góry ustalonych nie występujących w tym równaniu Ki: ![]()
.
Warunkiem koniecznym i dostatecznym, aby pewne równanie modelu o m równaniach łącznie współzależnych było identyfikowalne jest, aby macierz utworzona ze współczynników przy zmiennych występujących w innych równaniach modelu i równocześnie nie występujących w i-tym równaniu była rzędu m-1. Jeżeli ten warunek jest spełniony i liczba zmiennych, które nie występują w tym równaniu (i występują w modelu) jest równa m-1, to równanie jest jednoznacznie identyfikowalne, zaś jeśli jest większa, to równanie jest niejednoznacznie identyfikowalne.
Warunek konieczny i dostateczny jest trudny do sprawdzenia, gdyż wymaga znajomości wartości ocen estymatorów parametrów, które w momencie badania identyfikowalności nie są jeszcze znane.
Przykład
Sprawdzimy identyfikowalność modelu
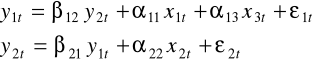
W postaci strukturalnej zapiszemy model jako

.
Z postaci macierzy B wynika, że jest to model o równaniach łącznie współzależnych.
Sprawdźmy identyfikowalność pierwszego równania.
Warunek konieczny: liczba zmiennych endogenicznych nieopóźnionych występujących w tym równaniu wynosi g1=2. Liczba zmiennych z góry ustalonych niewystępujących w tym równaniu wynosi K1=1, zatem spełniony jest warunek konieczny ![]()
.
Warunek konieczny i dostateczny: macierz utworzona ze współczynników przy zmiennych występujących w innych równaniach modelu i równocześnie nie występujących w 1. równaniu ma postać [-α22] i jej rząd jest równy 2-1=1 o ile α22≠0. Jednocześnie, ponieważ tylko jedna zmienna nie występuje w tym równaniu wynosi 1, to jest to równanie identyfikowalne jednoznacznie.
Dla drugiego równania liczba zmiennych endogenicznych nieopóźnionych występujących w tym równaniu wynosi g1=2. Liczba zmiennych z góry ustalonych niewystępujących w tym równaniu wynosi K2=2, zatem spełniony jest warunek konieczny ![]()
.
Warunek konieczny i dostateczny: macierz utworzona ze współczynników przy zmiennych występujących w innych równaniach modelu i równocześnie nie występujących w 1. równaniu ma postać ![]()
i jej rząd jest równy 2-1=1 o ile α11≠0 lubα13≠0. Ponieważ w tym równaniu nie występują dwie zmienne, to jest to równanie identyfikowalne niejednoznacznie.
Omawiany model jest zatem identyfikowalny niejednoznacznie.
Przykład
Określimy teraz identyfikowalność równań modelu
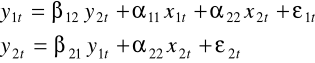
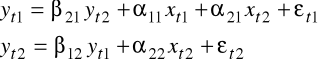
W postaci strukturalnej zapiszemy model jako
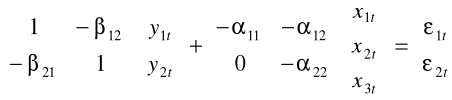
.
Z postaci macierzy B wynika, że jest to model o równaniach łącznie współzależnych.
Sprawdźmy identyfikowalność pierwszego równania.
Warunek konieczny: liczba zmiennych endogenicznych nieopóźnionych występujących w tym równaniu wynosi g1=2. Liczba zmiennych z góry ustalonych niewystępujących w tym równaniu wynosi K1=0, zatem nie jest spełniony warunek konieczny ![]()
. To równanie jest zatem nieidentyfikowalne.
Również warunek konieczny i dostateczny nie jest spełniony, gdyż macierz utworzona ze współczynników przy zmiennych występujących w innych równaniach modelu i równocześnie nie występujących w tym równaniu jest macierzą pustą i ma rząd równy zero.
Dla drugiego równania liczba zmiennych endogenicznych nieopóźnionych występujących w tym równaniu wynosi g1=2. Liczba zmiennych z góry ustalonych niewystępujących w tym równaniu wynosi K2=1, zatem spełniony jest warunek konieczny ![]()
.
Warunek konieczny i dostateczny: macierz utworzona ze współczynników przy zmiennych występujących w innych równaniach modelu i równocześnie nie występujących w 1. równaniu ma postać [-α11] i jej rząd jest równy 2-1=1 o ile α11≠0. Ponieważ w tym równaniu nie występuje jedna zmienna, to jest to równanie jednoznacznie identyfikowalne.
W omawianym modelu tylko jedno równanie jest identyfikowalne, zaś model jest modelem nieidentyfikowalnym.
Estymacja modeli wielorównaniowych
Metoda estymacji parametrów modeli wielorównaniowych zależy od rodzaju powiązań między zmiennymi oraz od identyfikowalności modelu.
Modele proste estymuje się przy pomocy KMNK, traktując każde równanie jako model jednorównaniowy.
Parametry modeli rekurencyjnych szacuje się, zgodnie z ich nazwą, rekurencyjnie.
Metoda szacowania parametrów modeli o równaniach łącznie współzależnych zależy od rodzaju powiązań między zmiennymi. Modele jednoznacznie identyfikowalne szacuje się stosując pośrednią metodę najmniejszych kwadratów (PMNK). Dla modeli niejednoznacznie identyfikowalnych stosuje się podwójną metodę najmniejszych kwadratów (2MNK).
Szacowanie parametrów modeli rekurencyjnych
W modelu rekurencyjnym szacuje się najpierw parametry równania, w którym zmienna objaśniana zależy tylko od zmiennych z góry ustalonych (przy przyjętych oznaczeniach ostatniego równania, w którym występuje tylko jedna zmienna endogeniczna nieopóźniona ym), stosując klasyczną MNK. Następnie wyznacza się z tego równania wartości teoretyczne tej zmiennej ![]()
i podstawia się je do kolejnego (poprzedniego) równania, traktując odtąd tę zmienną tak jak zmienną z góry ustaloną. W ten sposób w kolejnym równaniu zmienna objaśniana zależy już tylko od zmiennych z góry ustalonych i szacuje się parametry tego równania przy pomocy KMNK.
Przykład
W omawianym poprzednio modelu produkcji
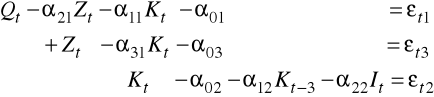
estymujemy najpierw parametry ostatniego równania wyznaczając
![]()
,
następnie parametry równania drugiego podstawiając za ![]()
:
![]()
i ostatecznie wyznaczamy parametry pierwszego równania jako:
![]()
.
Pośrednia MNK
W PMNK szacuje się parametry modelu dla postaci zredukowanej, a następnie przekształca się je na oceny parametrów postaci strukturalnej. Metodę tę można stosować jedynie do modeli lub równań jednoznacznie identyfikowalnych.
Przykład
Weźmy pod uwagę jednoznacznie identyfikowalny model:
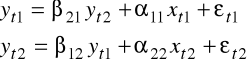
,
o postaci strukturalnej
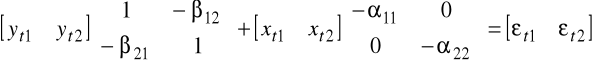
Ponieważ 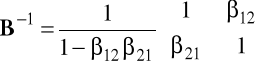
, zatem postać zredukowana modelu jest następująca:
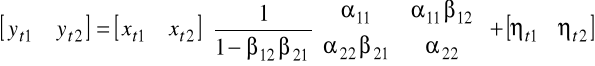
.
Załóżmy, że oszacowania postaci zredukowanej mają wartości np.:
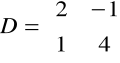
.
Wówczas
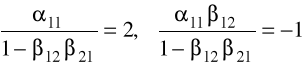
,
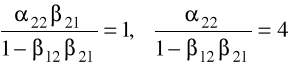
.
ze stosunku odpowiednich stron równań w obu wierszach mamy
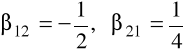
i podstawiając te wartości np. do pierwszej i ostatniej z zależności mamy
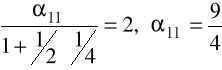
,
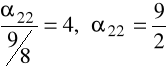
.
Zatem oszacowanie postaci strukturalnej tego modelu przedstawia się jako
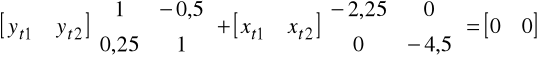
.
Podwójna MNK
W podwójnej metodzie najmniejszych kwadratów (2MNK) dwukrotnie stosuje się MNK. Metodę tę stosuje się do modeli o równaniach łącznie współzależnych niejednoznacznie identyfikowalnych.
W pierwszym kroku szacuje się parametry postaci zredukowanej modelu przy pomocy MNK. Na podstawie tych ocen wyznacza się wartości teoretyczne nieopóźnionych zmiennych endogenicznych. Wartości te wprowadza się do równań postaci strukturalnej i traktuje te zmienne jako zmienne z góry ustalone.
Następnie szacuje się parametry postaci standardowej (ewentualnie uzyskując ją z odpowiednio przekształconej postaci strukturalnej) ponownie wykorzystując MNK.
Przykład
Oszacujmy parametry modelu z jednego z omawianych przykładów, przyjmując w pierwszym równaniu zmienną xt1 jako stale równą 1 (wyraz wolny):
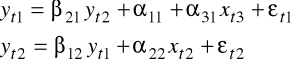
o postaci strukturalnej
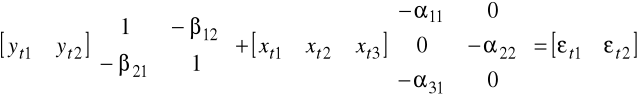
.
Parametry modelu oszacujemy na podstawie danych
t |
xt2 |
xt3 |
yt1 |
yt2 |
1 2 3 4 5 6 7 8 |
1 3 2 1 5 2 1 4 |
3 5 1 2 3 2 2 1 |
2 5 5 6 4 1 3 4 |
3 1 6 5 2 3 4 1 |
Podany model, jak już stwierdzono (niezależnie od tego, że zmienna xt1 przyjmuje stałe wartości!), jest niejednoznacznie identyfikowalny.
Oszacujemy parametry tego modelu podwójną MNK.
Macierz
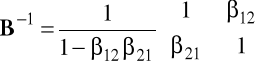
,
zatem postać zredukowana modelu jest następująca:
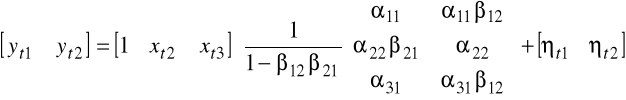
, czyli
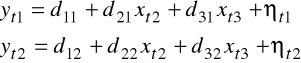
.
Macierz obserwacji zmiennych objaśniających i wektory obserwacji zmiennych objaśnianych są następujące:
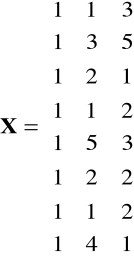
, 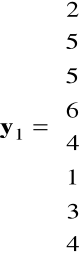
, 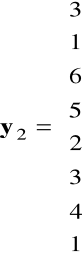
.
zatem dla pierwszego równania
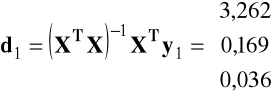
oraz dla drugiego równania
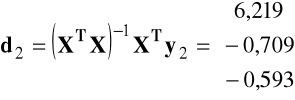
.
Podstawiamy te wartości do postaci strukturalnej i wyznaczamy wartości teoretyczne ![]()
i ![]()
:
t |
|
|
1 |
3,541 |
3,730 |
2 |
3,951 |
1,124 |
3 |
3,636 |
4,207 |
4 |
3,504 |
4,323 |
5 |
4,216 |
0,892 |
6 |
3,673 |
3,614 |
7 |
3,504 |
4,323 |
8 |
3,974 |
2,788 |
Powracając do postaci standardowej (która była w tym przypadku postacią wyjściową modelu) podstawiamy
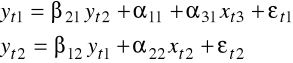
,
tzn. dla pierwszego równania odpowiednie macierze w tym przypadku przyjmą postać
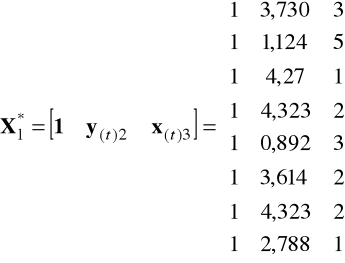
, 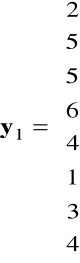
i stosując do tego równania KMNK otrzymujemy wektor ocen parametrów
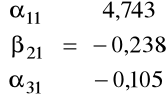
,
zaś dla drugiego równania mamy macierze
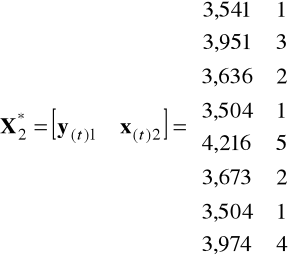
, 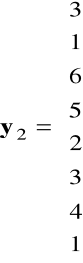
i wektor ocen estymatorów parametrów
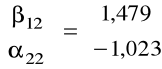
zatem ostatecznie model zostaje oszacowany jako
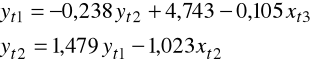
.
Wyszukiwarka