4.Uproszczenie Stokesa, Oseena i Prandtla.
Trudności matematyczne w rozwiązaniu pełnego układu równań opisujących ruch cieczy lepkiej przyczyniły się do poszukiwań uproszczonych form wspomnianych równań.
Równania Naviera Stokesa w swej postaci ogólnej są różniczkowymi równaniami nieliniowymi o pochodnych cząstkowych drugiego rzędu. Zawierają one cztery zmienne niezależne: trzy składowe prędkości i składową ciśnienia.
Rozróżniamy trzy podstawowe formy uproszczone równań Naviera Stokesa:
- uproszczenie Stokesa,
- uproszczenie Oseena
- uproszczenie Prandtla
Uproszcenia Stokesa i Oseena mogą być stosowane tylko w zakresie małych
liczb Reynoldsa(Liczba ta pozwala oszacować występujący podczas ruchu płynu stosunek sił czynnych (sił bezwładności) do sił biernych związanych z tarciem wewnętrznym w płynie przejawiającym się w postaci lepkości.), zatem dotyczą one bardzo powolnych przepływów, stosuje się je do zagadnień dotyczących opływu ciał strumieniem jednorodnym w nieskończoności. Uproszczenie Stokesa otrzymano w wyniku odrzucenia nieliniowego członu reprezentującego przyspieszenie tzn. pominięto w rozważaniach całą lewą stronę w równaniu Naviera Stokesa .
Równanie Oseena otrzymano poprzez zlinearyzowanie nieliniowego członu reprezentującego przyspieszenie w równaniu Nawiera Stokesa.
Uproszczenie Prandtla opiera się na koncepcji warstwy przyściennej i obowiązuje ono w zakresie dużych liczb Reynoldsa, a więc dotyczą one szybkich przepływów.
4.1 Uproszczenie Stokesa.
Uproszczenia Stokesa polegała na tym, że w przypadku powolnego ruchu ciała w cieczy o dużej lepkości, siły spowodowane lepkością są znacznie większe od sił masowych, proporcjonalnych do przyspieszenia. Stokes badając opływ kuli cieczą lepką uznał, że w swych badaniach może pominąć wpływ całej lewej strony równania Naviera Stokesa na obraz przypływu.
Zakładając, że ![]()
, otrzymał Stokes następujący układ równań:
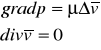
(1) i (2)
Równanie (1) nazywamy równaniem Stokesa.
Rozpisując układ równań (1) i (2) na składowe otrzymamy:
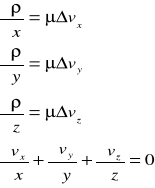
(3)
Układ równań (3) jest układem zamkniętym, zawiera 4 równania i 4 funkcje niewiadome:
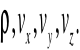
W przypadku opływu ciała strumieniem jednorodnym w nieskończoności warunki brzegowe maja następującą postać:
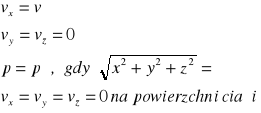
(4)
Stokes rozwiązując układ równań (3) wraz z warunkami brzegowymi (4) określił pole prędkości i ciśnień i na tej podstawie otrzymał wzór na opór kuli:
![]()
(5)
Zwany wzorem Stokesa;
Gdzie R- oznacza promień kuli.
Z wzoru (5) wynika, że opór kuli występujący w ruchu względnym w ośrodku płynnym jest proporcjonalny do pierwszej potęgi prędkości. Wzór ten może być także stosowany do badania ruchu płynów zawierających zawiesiny, a więc do ośrodków niejednorodnych.
Wprowadzając współczynnik oporu:
![]()
(6)
Oraz liczbę Reynoldsa
Re=![]()
Otrzymamy następujący wzór
![]()
(7)
Wzór ten jest słuszny tylko dla bardzo małych liczb Reynoldsa (Re![]()
1) rzędu 0,3.
Trzeba zwrócić uwagę na wewnętrzną sprzeczność, tkwiącą w zagadnieniu opływu kuli opisanym układem równań (3) oraz warunkami brzegowymi (4), odniesionymi do opływu walca o dowolnym przekroju. Okazuje się bowiem, że nie mogą być spełnione równocześnie warunki brzegowe na powierzchni ciała i w nieskończoności. Te właściwość zagadnienia określonego zależnościami (3) i (4), nazywamy paradoksem Stokesa.
Pyzatym, okazuje się, że siły masowe, które zostały odrzucone z założenia w równaniu rządzącym przepływu płynu jako wielkości małe w porównaniu z siłami lepkości, w dostatecznie dużej odległości od opływanego ciała stają się większe od sił lepkości.
Odrzucenie sił masowych jest również możliwe w przypadku przepływów powolnych, ale tylko w obszarach bliskich ścianek ciała stałego.
4.2 Uproszczenie Oseina.
Oseen prowadząc badania dotyczące powolnego ruchu ciała stałego w cieczy o dużej lepkości stwierdził, że nie wszystkie składniki siły masowej związane z przyspieszeniem są pomijalnie małe, bowiem niektóre z nich w dość dużej odległości od ciała są duże w porównaniu z pozostałymi.
Przyjmując, że oś x ma kierunek i zwrot ![]()
, to składowe prędkości w dostatecznie dużej odległości od ciała mogą być wyrażone zależnościami:
![]()
![]()
![]()
(8)
Gdzie wielkości oznaczone indeksem ` w równaniu (8) są małe w porównaniu z ![]()
, zatem:
![]()
<<1; ![]()
<<1; ![]()
<<1 (9)
Rozwijając w równanie Naviera Stokesa poszczególne składowe otrzymamy:
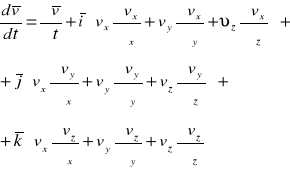
(10)
Podstawiając wzór (8) do (10) dostaniemy:
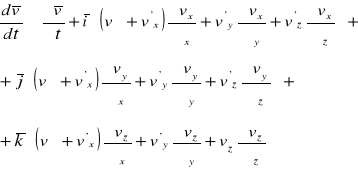
(11)
Wykonując następnie mnożenia dostaniemy:
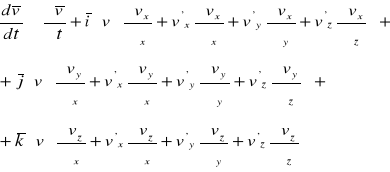
(12)
Na mocy założenia (8) i (9) można przyjąć, że pierwszy składnik każdego wyrażenia będącego w nawiasie będzie większy od pozostałych, zatem otrzymamy:
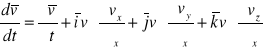
Ostatecznie po przekształceniach otrzymamy:
![]()
(13)
Wprowadzając zależność (13) do równania Naviera stokesa, Oseen uzyskał równanie liniowe dla ruchu stacjonarnego, zwane dzisiaj równaniem Oseena:
![]()
(14)
Oseen rozwiązując następujący układ równań:
![]()
![]()
(15)
Przy uwzględnieniu warunków brzegowych zaproponowanych przez Stokesa
![]()
(16)
oraz ![]()
na powierzchni ciała
do wyznaczenia opływu kuli, uzyskał wzór na współczynniki oporu kuli, wzór ten nosi nazwę wzoru Oseena
![]()
![]()
(17)
W tym przypadku nie występuje paradoks Stokesa w odniesieniu do równania Ossena (14) zatem można uzyskać rozwiązanie dla płaskiego zagadnienia określonego równaniem (15) i warunkami brzegowymi (16) dotyczącego opływu ciał walcowych strumieniem cieczylepkiej.
4.3 Uproszczenie Parnadtla.
Uproszczenie Parnadtla opiera się na koncepcji warstwy przyściennej i obowiązuje ono w zakresie dużych liczb Reynoldsa, a więc szybkich przepływów.
Parndtl w swoich badaniach stwierdził, że całkowity obszar przepływu wokół opływanego ciała stałego cieczą lepką można podzielić na dwa podobszary.
Gdy jeden podobszar przylega bezpośrednio do ścianek opływanego ciała stałego i charakteryzuje się , tym, że lepkość cieczy w sposób istotny ma wpływ na charakter przepływu; siły lepkości odgrywają tutaj dominująca rolę. Są one szczególnie duże -ponieważ wyjątkowo duży jest gradient prędkości wzdłuż normalnej do przepływu, wynika to z faktu, że na małym odcinku prędkości przepływu musi wzrosnąć od wartości ![]()
=0 do wartości ![]()
, a więc do prędkości przepływu niezakłóconego. Ten podobszar Prandtl nazwał warstwą przyścienną. Ruch opisują tutaj równania Prandtla.
Drugi podobszar znajduje się poza warstwa przyścienną , wpływ lepkości cieczy na charakter przepływu jest pomijalnie mały, natomiast znaczącą rolę odgrywają siły masowe. Ciecz w tym podobszarze możemy traktować jako doskonałą, a jej ruch możemy opisać za pomocą równań Eulera.
Grubością warstwy przyściennej ![]()
nazywamy odległość od konturu ciała do granicy warstwy przyściennej.
Granica warstwy przyściennej przechodzi przez te punkty w których prędkość przepływu różni się o 1% od ![]()
, zatem.
![]()
Zależność ta określa prędkość przepływu na granicy warstwy przyściennej.
Wyszukiwarka