Grupa laboratoryjna: 204 Nr ćwiczenia: 66

W skład grupy wchodzą:

Temat ćwiczenia:

Wyznaczanie stałej Plancka

Wydział: Ochrona Środowiska

Semestr: Drugi

Studia: Dzienne-Inżynieskie

Promieniowaniem termicznym nazywamy emisję fal elektromagnetycznych przez ciało po odpowiednim ogrzaniu. Niewielka część fal pokrywa się ze światłem widzialnym, reszta pokrywa się z podczerwienią.

Wielkościami charakteryzującymi promieniowanie termiczne są:

zdolność emisyjna e(,T)d - która jest energią promieniowania wysyłanego w jednostce czasu z jednostki powierzchni o temperaturze T, w postaci fal elektromagnetycznych o częstościach zawartych w przedziale od do +d.

zdolność absorbcyjna a(,T) - określa jaka część energii fali elektromagnetycznej o częstościach zawartych w przedziale od do +d, padającej na jednostkę powierzchni ciała pozostaje pochłonięta.

Prawo Kirchhoffa określa nam zdolność emisyjną ciała doskonale czarnego jako stosunek zdolności emisyjnej do zdolności absorbcyjnej i wyraża się wzorem:

Prawo Wiena mówi, że częstotliwość przy której zdolność emisyjna przyjmuje wartość maksymalną jest równa iloczynowi pewnej stałej i temperatury :

maź=constT

Prawo Stefana-Boltzmana mówi, że całkowita energia wypromieniowana przez jednostkową powierzchnię w jednostce czasu jest proporcjonalna do czwartej potęgi temperatury:

E=T

W celu wyjaśnienia rozkładu energii w widmie promieniowania ciała doskonale czarnego Max Planck wysunął hipotezę, że energia nie zmienia się w sposób ciągły lecz porcjami, które nazwał kwantami energii. Energia kwantu jest wprost proporcjonalna do częstości emitowanego promieniowania:

E=h

Zjawisko fotoelektryczne polega na emisji elektronów z metalu pod wpływem padającego światła. Na podstawie doświadczeń stwierdzono kilka faktów.

Energia wybijanych fotoelektronów nie zależy od natężenia padającego światła lecz od jego częstotliwości.

Dla każdego materiału istnieje pewna graniczna wartość częstotliwości przy której zaczyna się emisja fotoelektronów.

Nie stwierdza się żadnego opóźnienia czasowego między padaniem światła, a emisją elektronów.

Cechy te sprzeczne są z klasyczną teorią falową. Dopiero w 1905 r. Albert Einstein wyjaśnił zjawisko fotoelektryczne. Stwierdził on że kwant energii może być przekazywany elektronowi tylko w całości. Foton posiadający energię E=h, która musi być większa od pracy wyjścia, wybija jeden elektron, przy czym część energii zużywana jest na wybicie elektronu, a reszta jest przekazywana elektronowi w postaci energii kinetycznej. Równanie Einsteina-Millikana ma postać:

h=W+Ekmax

Korzystając z tego równania można wyznaczyć stałą Plancka. Metodę wyznaczania stałej Plancka przedstawia powyższy schematyczny rysunek.

Jest to przykład fotokomórki składającej się z fotokatody i fotoanody zamkniętych w szklanej rurce. Przez małe okienko wpada światło monochromatyczne i oświetla katodę. Początkowo wybijane elektrony docierają do anody i powodują, że pojawia się prąd nasycenia. Jeśli jednak pomiędzy fotokatodę i fotoanodę przyłożone jest napięcie hamujące (potencjał ujemny przyłożony do anody, a potencjał dodatni do katody) mniej elektronów będzie docierać do fotoanody. W układzie tym woltomierz V mierzy napięcie hamujące, a amperomierz A mierzy prąd anodowy.

Jeśli przez U0 oznaczymy wartość napięcia hamującego przy którym prąd anodowy jest równy zero to maksymalna energia kinetyczna będzie równa:

Ekmax=eU0

gdzie e jest ładunkiem elektronu.

Podstawiając do równania Einsteina-Millikana otrzymujemy wyrażenie:

eU0=h-W

Wykres napięcia hamującego w funkcji częstotliwości (y=ax+b) jest funkcją liniową o współczynnikach

.

Znając współczynniki a i b można wyznaczyć stałą Plancka i pracę wyjścia elektronów z metalu.

Przebieg ćwiczenia.

1. Przy napięciu hamowania Uh=0 mierzymy wartość prądu anodowego w zależności od długości fali.

Wartość prądu anodowego liczymy z prawa Ohma

które po przekształceniu daje nam
.

wiedząc że R=2.49 M, oraz mierząc potencjał U=0.0540 V i podstawiając do wzoru otrzymujemy natężenie anodowe

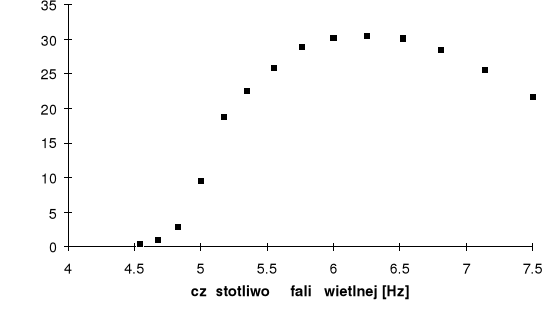
Tabela 1.

	nm		400	420	440	460	480	500	520	540
	Hz	1014	7.5	7.14	6.81	6.52	6.25	6	5.76	5.55
I	nA		21.6	25.5	28.5	30.1	30.5	30.2	28.9	25.9
	nm		560	580	600	620	640	660
n	Hz	1014	5.35	5.17	5	4.83	4.68	4.54
I	nA		22.5	18.8	9.6	2.9	0.96	0.36

Częstotliwość wyliczamy ze wzoru

, gdzie c jest prędkością światła, a długością fali świetlnej.

.

Obliczamy wartości oraz Ia dla długości fali pomiędzy 400 nm a 660 nm i wpisujemy do tabeli 1.

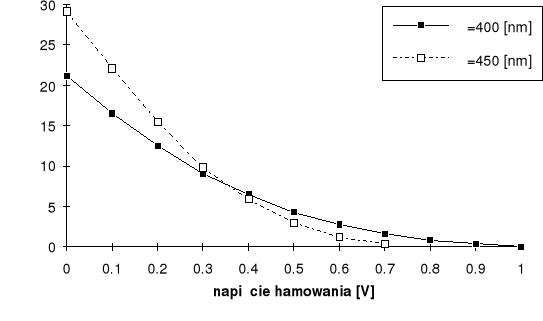
2. Dla określonych długości fali (400,450,500,550,600 nm) zdejmujemy krzywe hamowania.

Nastawiamy odpowiednią długość fali. Najpierw odczytujemy wartość prądu anodowego przy napięciu hamowania równym zero. Potem napięcie hamowania zwiększamy o 0.1V i odczytujemy wartość prądu anodowego.

Wartości wpisujemy do tabeli 2.

Tabela 2.

=	400nm	=	450 nm	=	500nm	=	550 nm	=	600nm
Uh	Ia	Uh	Ia	Uh	Ia	Uh	Ia	Uh	Ia
V	nA	V	nA	V	nA	V	nA	V	nA
0	21.2	0	29.2	0	30.3	0	24.3	0	9.3
0.1	16.5	0.1	22.1	0.1	21.1	0.1	15.3	0.1	4.8
0.2	12.5	0.2	15.5	0.2	12.7	0.2	8.1	0.2	1.8
0.3	9.1	0.3	9.8	0.3	6.3	0.3	2.7	0.3	0.3
0.4	6.5	0.4	5.9	0.4	2.6	0.4	0.6	0.4
0.5	4.3	0.5	3	0.5	0.72	0.5		0.5
0.6	2.8	0.6	1.2	0.6	0.04	0.6		0.6
0.7	1.6	0.7	0.4	0.7		0.7		0.7
0.8	0.8	0.8		0.8		0.8		0.8
0.9	0.36	0.9		0.9		0.9		0.9
1	0.04	1		1		1		1

Na końcu odczytujemy wartość napięcia hamującego przy którym prąd anodowy równy jest zero.

Wartości te wpisujemy do tabeli 3.

Tabela 3.

	nm	400	450	500	550	600
Uh	V	1.029	0.8	0.617	0.489	0.38

3. Wykreślamy zależność Ia=f()

4. Wykreślamy zależność Ia=f(Uh) dla poszczególnych długości fali.

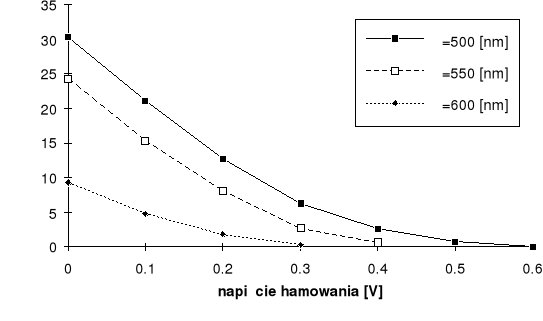
5. Wykorzystując program komputerowy obliczamy współczynniki a i b funkcji liniowej U=a+b i wykreślamy jej wykres.

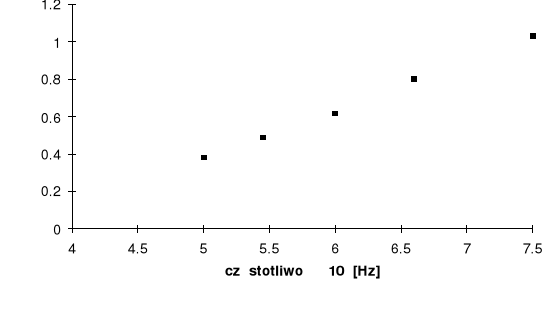
Obliczone wartości wynoszą :

a=2.6410-15, b= -0.93

wykorzystując zależności h=ae oraz W=-be otrzymujemy wartości stałej Plancka h oraz pracy wyjścia W:

h=2.6410-151.610-19=4.22410-34, W=0.931.610-19=1.44810-19

Ostateczne wyniki wynoszą

h=4.22410-34 Js oraz W=1.44810-19 J

Wyznaczanie stałej Plancka

3

---