TEORIA BŁĘDÓW POMIARU
Cel pomiaru: poznanie wartości rzeczywistej wielkości mierzonej
ograniczona dokładność narzędzi pomiarowych i metoda pomiaru
zmienność warunków fizycznych, w których odbywa się pomiar
niedostateczna znajomość obiektu pomiaru
niedostateczne kwalifikacje obserwatora
↓
błąd pomiaru
wartość otrzymana ≠ wartość rzeczywista
w wyniku pomiaru wielkości mierzonej
LICZBOWE MIARY BŁĘDÓW POMIARU
• Błąd bezwzględny
![]()
Xm -wartość mierzona
Xr - wartość rzeczywista
Xr → wartość poprawna Xp
Rolę wartości poprawnej Xp może pełnić:
- wynik pomiaru uzyskany za pomocą dokładniejszego przyrządu pomiarowego lub za pomocą dokładniejszej metody pomiarowej
- średnia arytmetyczna wyników serii pomiarów
- wartość obliczona na podstawie przesłanek teoretycznych
Błąd bezwzględny
![]()
• Poprawka
![]()
![]()
• Błąd względny
![]()
Często stosuje się przybliżenie
![]()
• Błąd zredukowany (zakresowy)
![]()
gdzie zakres pomiarowy Xn :
![]()
• Klasa dokładności
dopuszczalny błąd podstawowy narzędzia pomiarowego
podany przez producenta
![]()
![]()
- dopuszczalny błąd bezwzględny
Xn - zakres pomiarowy
Np. Błąd pomiaru miernikiem nie jest większy niż Δd
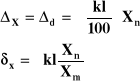
Rodzaje bŁędów pomiarów
ze względu na źródła ich powstawania
błędy spowodowane przez przyrządy pomiarowe
błędy spowodowane przez metody pomiarowe
błędy spowodowane przez obserwatora
błędy spowodowane przez obliczenia
błędy spowodowane przez wpływy otoczenia
KLASYFIKACJA BŁĘDÓW POMIARÓW
Kryterium klasyfikacji |
|
Charakter błędu |
- błąd systematyczny - błąd przypadkowy - błąd nadmierny |
Warunki fizyczne pomiaru |
- błąd podstawowy - błędy dodatkowe |
Charakter wielkości mierzonej |
- błędy statyczne - błędy dynamiczne |
Fizyczne przyczyny błędu (źródła błędu) |
- błąd wzorcowania - błąd niestałości wielkości mierzonej - błędy dodatkowe - błąd dynamiczny - błąd kwantowania - błąd próbkowania - błąd zliczania - błąd metody - błąd odczytu itd. |
Zależność błędu od wielkości mierzonej |
- błąd addytywny - błąd multiplikatywny |
BŁĘDY SYSTEMATYCZNE
To błędy, które przy wielu pomiarach tej samej wartości pewnej wielkości, wykonywanych w tych samych warunkach, pozostają stałe zarówno, co do wartości bezwzględnej, jak
i znaku lub zmieniają się wg określonego prawa wraz ze zmianą warunków otoczenia.
Błędy te modeluje się za pomocą zmiennej zdeterminowanej
(przyczyna → zdeterminowany skutek)
Błędy te można całkowicie lub częściowo wyeliminować
z wyniku pomiaru za pomocą poprawek, które oblicza się teoretycznie lub wyznacza doświadczalnie.
Przyczyny występowania błędów systematycznych:
błędy podstawowe narzędzi pomiarowych (podawane jako błędy graniczne)
uproszczony model konstrukcji i niedoskonałość
wykonania przyrządu, błędy wzorcowania
oddziaływanie przyrządu pomiarowego na wielkość mierzoną - błędy metody pomiarowej
np. pobór energii ze źródła mierzonego przez przyrządy pomiarowe
wpływ warunków zewnętrznych (wielkości wpływających) błędy dodatkowe
Ilustracja powstawania błędu metody
I - wartość rzeczywista natężenia prądu stałego
I' - wartość natężenia prądu stałego wskazana przez miernik
I' < I gdy RA > 0
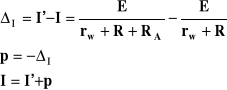
Wynik końcowy:
![]()
ΔA - błąd dopuszczalny amperomierza:
dla przyrządu analogowego ![]()
dla przyrządu cyfrowego ![]()
In - zakres pomiarowy amperomierzaOkreślanie błędów systematycznych w pomiarach
a) bezpośrednich b) pośrednich
Pomiary bezpośrednie
w warunkach normalnych:
X = Xm ± Δd
Δd błąd dopuszczalny narzędzia pomiarowego
w warunkach, które różnią się od normalnych:
X = (Xm+ ∑p) ± Δd
Xm+ ∑p wynik pomiaru poprawiony przez usunięcie błędów dodatkowych
gdy błędów dodatkowych nie można wyeliminować za pomocą poprawek
X = Xm ± Δx
Δx = ± [Δd + ∑ Δdd]
Δd błąd dopuszczalny narzędzia pomiarowego
Δdd dopuszczalny błąd dodatkowy
Pomiary pośrednie
Założenie: błędy przypadkowe są pomijalnie małe
Poszukiwana wielkość Y jest funkcją n wzajemnie niezależnych wielkości pomiarowych X1, X2, ... , Xn , tzn.
Y=f(X1, X2, ... , Xn)
Jeżeli X1, X2, ... , Xn wyznaczono z błędami bezwzględnymi odpowiednio ΔX1, ΔX2, ... , ΔXn i wartości tych błędów są małe,
to wypadkowy błąd ΔY oraz błąd δY można wyznaczyć:
metodą przyrostów
metodą różniczki zupełnej
Metoda przyrostów
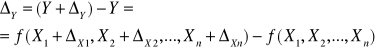
W praktyce metoda ta jest rzadko stosowana z uwagi
na bardzo pracochłonne obliczenia.
Metoda różniczki zupełnej
W celu wyjaśnienia podstaw matematycznych tej metody rozważmy powstawanie błędu przy określaniu wartości wielkości Y , spowodowanego niedokładnym wyznaczeniem tylko jednej wielkości pomocniczej np. X1 - tj. ΔX1
Zakłada się, że wartości pozostałych wielkości są zmierzone bezbłędnie i wielkości te nie ulegają zmianie w czasie pomiaru.
Wartość wielkości Y zamiast Y=f(X1, X2, ... , Xn) wynosi
Y+ΔY= f(X1+ΔX1, X2, ... , Xn)
Jeżeli funkcja ta jest ciągła to można ją rozwinąć w szereg Taylora
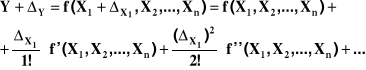
Przy małych ΔX1 można pominąć wyrazy szeregu, które zwierają ΔX1 wyższych potęgach
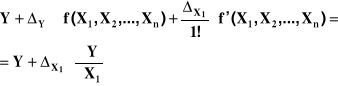
Błąd systematyczny pomiaru wielkości Y oblicza się na podstawie błędów systematycznych mierzonych wielkości
X1, X2, ... , Xn zgodnie z prawem liniowej propagacji błędu
- w przypadku, gdy błędy systematyczne są znane co wartości i znaku
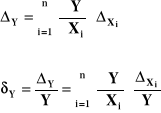
- w przypadku, gdy znane są tylko błędy graniczne pomiarów
bezpośrednich ΔXgi („najgorszy przypadek”)
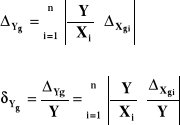
Wyznaczanie błędów granicznych dla wielkości Y prowadzi
do wyników zawyżonych, bowiem bardzo małe jest prawdopodobieństwo takiego zdarzenia, w którym błędy systematyczne wszystkich wielkości pomocniczych jednocześnie przyjmują wartości graniczne i niekorzystny układ znaków.
W pomiarach pośrednich błędy systematyczne dla poszczegól-nych wielkości pomocniczych układają się losowo i niezależnie
Błąd wypadkowy można obliczać także jako tzw. błąd średni kwadratowy (jego wartość jest bardziej prawdopodobna i nie przekracza wartości błędu granicznego).
błąd średni kwadratowy
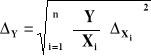
PODSUMOWANIE
W procesie pomiaru występują zarówno błędy systematyczne,
jak i błędy przypadkowe.
W praktyce, jeżeli wartości błędów przypadkowych nie przekraczają 1/10 wartości błędu całkowitego, to można przyjąć, że błędy przypadkowe są pomijalnie małe w odniesieniu do błędów przypadkowych.
Ilustracja klasyfikacji błędów - rezultat strzelania do tarcz
Reprezentacja błędu : odległość między śladem przejścia kuli
a środkiem tarczy
rw
R
RA
E
I =?
rw
Z
Z
Z
I'
R
A
X
Y
E
SYSTEM
POMIAROWY
Obiekt
Pomiaru
Wyszukiwarka