Proces inwestowania w rolnictwie
Inwestowaniem nazywamy nakłady gospodarcze, których rolą jest tworzenie nowych lub powiększanie istniejących potencjałów wytwórczych oraz majątku nieprodukcyjnego. W ślad za tym rozróżniamy inwestycje produkcyjne i nieprodukcyjne.
Nakłady inwestycyjne są to środki rzeczowe i finansowe związane z zakupem i budową nowych oraz rekonstrukcją i rozbudową istniejących składników trwałego majątku produkcyjnego. Analizować można je w skali przedsiębiorstwa (ujęcie mikroekonomiczne) lub też wyodrębnionego sektora i całej gospodarki narodowej (ujęcie makroekonomiczne).
Potencjały gospodarcze (środki trwałe) sukcesywnie zużywają się, wobec czego - w celu podtrzymania ich zdolności produkcyjnej i usługowej - muszą być odtwarzane. Odtwarzanie (restytucja) następuje z odpisów amortyzacyjnych, które są proporcjonalne do wartości zużycia środków w danym czasie. Nie zwiększa ono istniejących potencjałów, a tylko służy podtrzymaniu ich dotychczasowej zdolności produkcyjnej (usługowej). Równocześnie z restytucją zużytych środków następuje tworzenie nowych potencjałów. W praktyce trudno jednak oddzielić od siebie procesy restytucji i tworzenia nowych potencjałów, gdyż zużyte środki na ogół nie bywają odtwarzane w ich pierwotnej postaci fizycznej. Na miejscu zużytych (wycofanych) środków pojawiają się jakościowo nowe, bardziej nowoczesne technicznie i ekonomicznie sprawniejsze. Środki pochodzące z odpisów amortyzacyjnych wykorzystywane są wprawdzie do odtwarzania wartości środków trwałych, lecz pod względem technicznym reprezentują nowe potencjały. Dlatego przyjęto uważać, że wszelkie nakłady - te które zmierzają do restytucji zużytego majątku i te, które tworzą nowe potencjały - traktuje się jako inwestycje. Rozpatrując je z wartościowego punktu widzenia wyróżniamy w nich inwestycje restytucyjne oraz inwestycje nowe, zwane także inwestycjami netto. Inwestycje restytucyjne odpowiadają prostej reprodukcji majątku, natomiast inwestycje netto określają wielkość reprodukcji rozszerzonej, a więc rzeczywisty przyrost potencjału wytwórczego. Suma inwestycji restytucyjnych i nowych (netto) daje inwestycje brutto. Jeśli nie zaznaczono inaczej, pojęcie inwestycji identyfikuje się z inwestycjami brutto.
Inwestycje w rolnictwie stanowią sumę nakładów inwestycyjnych brutto poniesionych we wszystkich jednostkach gospodarczych tego sektora w danej jednostce czasu, tj. w ciągu roku. Specyficzną cechą rolnictwa jest duży udział tzw. inwestycji naturalnych. Wprawdzie, w odróżnieniu od przemysłu, rolnictwo wytwarza stosunkowo niewiele dóbr inwestycyjnych (jest to właściwie tylko zarodowy inwentarz żywy oraz materiał szkółkarski), ale w trakcie wykonywania inwestycji w gospodarstwach rolnych ponoszone są nakłady pracy samych rolników oraz nakłady żywej siły pociągowej i ziemi. Suma wartości wszystkich tych nakładów, występujących najczęściej w formie naturalnej, określana jest mianem inwestycji naturalnych. W innych ogniwach agrobiznesu, poza rolnictwem, inwestycje te występują sporadycznie.
Inwestowanie w agrobiznesie
Są dwa ważne powody inwestowania w agrobiznesie:
tworzenie nowych potencjałów w celu zwiększenia produkcji lub; usług, podniesienia ich jakości oraz obniżenia kosztów;
uczynienie pracy ludzkiej lżejszą, bezpieczniejszą, bardziej wydajną.
Inwestowanie nie jest jedynym sposobem osiągania tych celów; istnieją także tzw. drogi bezinwestycyjne, polegające na wprowadzaniu usprawnień technicznych i organizacyjnych, a więc ulepszaniu zarządzania.
Jedną z zasad racjonalnego gospodarowania w agrobiznesie jest wykorzystywanie najpierw wszelkich możliwych źródeł bezinwestycyjnego zwiększania produkcji i poprawy warunków pracy. Trzeba przede wszystkim wykorzystać te możliwości, jakie stwarza istniejący już potencjał, a dopiero po ich wyczerpaniu sięga się po nakłady inwestycyjne. Tak więc, metody inwestycyjne stosuje się wtedy, gdy danych celów gospodarczych nie można osiągnąć środkami bezinwestycyjnymi.
Rozpatrując nakłady inwestycyjne z punktu widzenia ich funkcji, wyróżnia się następujące:
inwestycje produktotwórcze typu ekstensywnego, tj. takie, które tworzą nowe potencjały produkcyjno-usługowe (np. zakup ziemi, inwestycje budowlane, zakup maszyn i urządzeń, instalowanie całych linii technologicznych, tworzenie zaplecza magazynowo-handlowego, zakup środków transportu itp.);
inwestycje produktotwórcze typu intensywnego, tj. takie, które podnoszą produktywność istniejących potencjałów (np. inwestycje w ziemię, które wywołują wzrost plonów, nakłady służące zwiększaniu produkcyjności zwierząt, nakłady modernizacyjne w rolnictwie i w przemyśle spożywczym, które podnoszą wydajność istniejącego potencjału itp.); inwestycje ograniczające straty surowców rolniczych, półproduktów i wyrobów gotowych, które powstają w różnych fazach procesu produkcyjnego;
inwestycje podnoszące jakość wytwarzanych produktów i świadczonych usług (np. nakłady modernizacyjne i nowe technologie, które podnoszą jakość produktów oraz ich użyteczność z punktu widzenia konsumenta, nakłady redukujące zawartość składników szkodliwych dla zdrowia człowieka itp.);
inwestycje sprzyjające obniżaniu kosztów wytwarzanych produktów lub świadczonych usług; są to zwykle nakłady typu intensywnego, których funkcją jest tworzenie technologii obniżających koszty nie tylko w skali przedsiębiorstwa, ale całego sektora żywnościowego; należy zauważyć, że występują takie nakłady inwestycyjne, które wprawdzie obniżają koszty w danym przedsiębiorstwie, lecz jednocześnie podnoszą koszty społeczne produkcji żywności (np. przedsiębiorstwo obniża swoje koszty emitując szkodliwe substancje do środowiska naturalnego i przerzuca koszty jego odnowy na całe społeczeństwo);
inwestycje usprawniające pracę ludzi i czyniące ją lżejszą oraz bardziej bezpieczną - nie wywołują one wprawdzie wymiernych efektów produkcyjno-kosztowych, ale poprawiają warunki pracy; przykładem mogą być inwestycje mechanizacyjne w rolnictwie, które wprawdzie nie powodują podniesienia plonów i wolumenu produkcji, lecz eliminują ciężką i niebezpieczną pracę ludzi (np. ciągniki, silniki elektryczne i spalinowe, zabezpieczenia przed szkodliwymi chemikaliami);
inwestycje podtrzymujące stan i zdolność produkcyjną ekosystemów rolniczych, a więc nakłady inwestycyjne w środowisko naturalne, których funkcją jest przeciwdziałanie entropii zasobów naturalnych szczególnie ważnych dla wytwarzania zdrowej żywności (gleba, woda, powietrze, las, zasoby genetyczne itp.).
Przedstawiony podział nakładów inwestycyjnych nie jest „ostry”; niektóre typy nakładów służą spełnianiu dwu lub nawet więcej funkcji. Tak np. inwestycje usprawniające pracę ludzi czynią ją bardziej wydajną i w ten sposób - pośrednio - sprzyjają obniżaniu kosztów. Liczne nakłady typu intensywnego sprzyjają także obniżaniu kosztów i podnoszeniu jakości produktów. W grupowaniu tym chodzi nie tyle o jednoznaczne zakwalifikowanie nakładu inwestycyjnego do jakiejś klasy, ile o wskazanie, jakie funkcje inwestycje mogą pełnić w agrobiznesie.
Formy reprodukcji środków trwałych
Rozróżniamy dwie formy reprodukcji środków trwałych: reprodukcję prostą oraz reprodukcję rozszerzoną. Istnieje również pojęcie reprodukcji ujemnej tj. dekapitalizacji.
In=(Ib+Rk) - a
gdzie:
In - inwestycje netto,
Ib - inwestycje brutto,
Rk - wartość (koszt) kapitalnych remontów,
a - amortyzacja.
Jeśli: Ib+Rk = a to In = 0
Ib+Rk > a In > 0
Ib+Rk < a In < 0
W pierwszym wypadku mamy do czynienia z reprodukcją prostą, w drugim - z reprodukcją rozszerzoną, a w trzecim - z reprodukcją ujemną środków trwałych, którą nazywamy dekapitalizacją.
Popyt inwestycyjny
Gospodarowanie czynnikami wytwórczymi w rolnictwie obejmuje również decyzje inwestycyjne. Decyzje te z jednej strony przesądzają alokację wolnych chwilowo zasobów kapitałowych, z drugiej zaś kreują nowe potencjały, które określają rozwój agrobiznes w przyszłości.
W gospodarce rynkowej popyt inwestycyjny składa się z dwu części:
inwestycji sektora prywatnego,
inwestycji sektora publicznego, w których decydujące miejsce zajmują wydatki państwa na dobra inwestycyjne.
W naszej gospodarce państwo jest jednym z ważnych inwestorów, a jego wydatki inwestycyjne określone są w budżecie. Poza tym państwo wprowadza uregulowania prawne i tworzy warunki stymulujące aktywność inwestycyjną sektora prywatnego. Wśród nich wymienić należy: politykę stopy procentowej od kredytów inwestycyjnych, ulgi inwestycyjne dla przedsiębiorstw, kredyty preferencyjne (np. dla rolników), ułatwienia w pozyskiwaniu kredytów zagranicznych i inne. Tak więc stwierdzamy, że chociaż działalność inwestycyjna jest domeną przedsiębiorstw, to jednak jest ona wielostronnie uwarunkowana makroekonomiczną polityką państwa. Agrobiznes poddany jest ogólnym warunkom inwestowania, które dyktuje rynek i ustawodawstwo powszechne, lecz w pewnych okolicznościach może on korzystać z ułatwień inwestycyjnych, jeśli jest to w interesie społecznym. Przykładem tych ostatnich są choćby kredyty preferencyjne dla rolników czy ulgi podatkowe udzielane określonym inwestorom.
W agrobiznesie występują:
inwestycje w kapitał ziemski (zakupy ziemi, regulacje stosunków wodnych w glebie, rekultywacja gruntów, infrastruktura techniczna związana bezpośrednio z ziemią);
inwestycje w kapitał trwały (zakupy maszyn i urządzeń produkcyjnych, budynki, budowle, oczyszczalnie ścieków, urządzenia redukujące emisję szkodliwych substancji do gleby, wody i powietrza);
inwestycje w zapasy (zapasy surowców, produkcji w toku i wyrobów gotowych).
W decyzjach inwestycyjnych, obojętne czego one dotyczą, zawsze trzeba porównać ze sobą przyszłe zyski (korzyści) z bieżącymi kosztami inwestycji. Porównaniom tym służy stopa procentowa. Jest ona jedną z ważniejszych zmiennych procesu inwestycyjnego. Od wysokości stopy procentowej zależy kształt i przebieg krzywej popytu inwestycyjnego.
Krzywa popytu inwestycyjnego (rys. 1) pokazuje zależność między planowanymi inwestycjami a poziomem stopy procentowej. Z rysunku 1 wynika, że jeśli stopa procentowa wzrośnie z r0 do r1; planowane inwestycje obniżą się z I0 do I1.
Rysunek 1. Krzywa popytu inwestycyjnego
Inwestycje w kapitał trwały i ziemski. W działalności inwestycyjnej mamy dwie sytuacje. Pierwszą wówczas, gdy inwestycja finansowana jest kredytem bankowym. Inwestycja musi wtedy przynieść zyski na tyle wysokie, aby mogły one spłacić zaciągnięty kredyt wraz z odsetkami. Drugą sytuację mamy wówczas, gdy inwestycja finansowana jest ze środków własnych przedsiębiorstwa. Wtedy inwestycja przynieść musi dochód co najmniej równy zyskom, które można osiągnąć, wykorzystując pieniądze przeznaczone na inwestycje w sposób alternatywny. Alternatywą może być ulokowanie kapitału w banku na znany procent lub udzielenie kredytu na określony procent innym firmom. W obu rozważanych tu sytuacjach - im wyższa jest stopa procentowa, tym wyższy musi być zwrot (zysk) z inwestycji. Inaczej mówiąc, zysk z inwestycji musi być co najmniej równy kosztowi alternatywnemu (utraconych możliwości) funduszy zamrożonych w nowych inwestycjach. Przy wysokiej stopie procentowej tylko niewiele projektów inwestycyjnych ma szansę realizacji. W miarę obniżania się stopy procentowej coraz więcej projektów zapewnia zwrot od kapitału co najmniej równy kosztowi utraconych możliwości funduszy przeznaczonych na inwestycje, a więc kosztowi alternatywnemu. Ta zależność wyjaśnia, dlaczego przy drogich kredytach, a więc przy polityce wysokiej stopy procentowej prowadzonej przez bank centralny, kurczy się front inwestycyjny. Sytuacja taka wystąpiła w polskim agrobiznesie w pierwszej połowie lat dziewięćdziesiątych.
Nachylenie krzywej popytu inwestycyjnego zależy od długości okresu „życia” danego obiektu inwestycyjnego. W przypadku inwestycji o długim jego okresie krzywa popytu inwestycyjnego jest bardziej spłaszczona aniżeli w przypadku obiektów żyjących krótko. Im dłuższy jest okres ekonomicznego życia obiektu, tym większy jest wpływ nawet niewielkiej zmiany stopy procentowej na opłacalność projektu inwestycyjnego. Wynika to z długości okresu zamrożenia nakładów inwestycyjnych. Im okres ten jest dłuższy, tym wyższy jest skapitalizowany (za pomocą procentu składanego) koszt początkowy obiektu inwestycyjnego zanim odzyska się zamrożony w nich kapitał.
Inwestycje w zapasy. Istnieją dwa rodzaje popytu inwestycyjnego w gospodarowaniu zapasami, mianowicie:
popyt spekulacyjny, kiedy przedsiębiorstwo nastawia się na zwyżkę cen i gromadzi zapasy surowców;
popyt transakcyjny, który wynika stąd, że wiele procesów produkcyjnych, szczególnie w agrobiznesie, jest rozłożonych w czasie i dla normalnego funkcjonowania przedsiębiorstwa (gospodarstwa) musi ono dysponować odpowiednimi zapasami.
Utrzymywanie większych zapasów może wówczas być źródłem korzyści, ale też pociąga za sobą koszty, gdyż zapasy oznaczają zamrożenie kapitału, na który trzeba zaciągać kredyt w banku na określoną stopę procentową. Podobnie więc jak w przypadku inwestycji w środki trwałe i ziemię, decydujące znaczenie ma tu wysokość stopy procentowej.
Inwestycje a rynek papierów wartościowych. Niektóre projekty inwestycyjne w agrobiznesie, i to projekty dużej skali, są finansowane nie przez normalne kredyty bankowe ani w postaci leasingu, lecz przez sprzedaż akcji firmy na rynku kapitałowym. Coraz więcej przedsiębiorstw sfery agrobiznesu w Polsce, zwłaszcza w przetwórstwie spożywczym i marketingu, ma postać spółek akcyjnych. Emisja akcji jest wówczas najdogodniejszym sposobem zdobycia środków na finansowanie inwestycji. Im wyższa jest cena jednej akcji, tym więcej środków zdoła firma zgromadzić z emisji. Cena akcji jest to w istocie zaktualizowana wartość strumienia oczekiwanych dywidend danej firmy, zdyskontowana przy określonej stopie procentowej. Wzrost stóp procentowych prowadzi przeto do spadku ceny akcji i ograniczenia skali inwestowania. Tak więc, nawet jeśli źródłem finansowania inwestycji są akcje, to krzywa popytu inwestycyjnego (rys. 1) nie zmienia swojego położenia. Jednocześnie wzrost oczekiwanych przyszłych zysków i dywidend, wywołujący wzrost cen akcji, prowadzi do zwiększenia rozmiarów inwestycji przy dowolnej stopie procentowej i przesuwa krzywą popytu inwestycyjnego w górę, dokładnie tak samo, jak w przypadku finansowania inwestycji przez kredyty bankowe.
Podsumowując nasze rozważania na temat popytu inwestycyjnego dochodzimy do dwu wniosków:
wzrost stopy procentowej zawsze wpływa na decyzje dotyczące inwestycji, w związku z czym krzywa popytu inwestycyjnego wyraża zależność rozmiarów planowanych inwestycji od poziomu stopy procentowej. W ten sposób decyzje mikroekonomiczne przedsiębiorstw sfery agrobiznesu są zdeterminowane makroekonomiczną polityką stóp procentowych.
wzrost kosztów dóbr kapitałowych albo spadek oczekiwanych zysków w przyszłości powoduje przesunięcie krzywej popytu inwestycyjnego w dół, i odwrotnie - spadek kosztów dóbr inwestycyjnych lub bardziej optymistyczna ocena perspektyw przyszłych zysków prowadzą do przesunięcia się krzywej w górę. Jeśli oczekiwania co do przyszłych zysków zmieniają się w dużej skali, przesunięcia krzywej popytu inwestycyjnego mogą być duże. Stabilność warunków gospodarowania w skali globalnej ma więc bardzo istotny wpływ na zachowanie się przedsiębiorstw (gospodarstw) sfery agrobiznesu.
Ocena efektywności inwestycji z uwzględnieniem czynnika czasu
Powszechnym zjawiskiem gospodarczym znanym wszystkim uczestniczącym w gospodarce rynkowej jest zmiana wartości pieniądza w czasie. Zmiany te występują w dwóch sytuacjach:
pierwsza dotyczy sytuacji kiedy składamy pieniądze w banku na czas określony, na tak zwany procent składany. Znając wartość początkował wielkość oprocentowania w skali roku można obliczyć przyrost środków pieniężnych po określonym czasie.
druga dotyczy sytuacji kiedy mamy do czynienia z przychodami będącymi efektem przedsięwzięcia inwestycyjnego, które występują w okresie użytkowania danej inwestycji. Nakłady inwestycyjne, np. na budowę obory, chlewni lub zakładu przetwórczego ponosimy w danym roku wyjściowym (niekiedy realizacja inwestycji trwa dwa lata lub dłużej), natomiast przychody z działalności produkcyjnej w nowych obiektach będą pojawiały się w kolejnych latach po oddaniu danego obiektu do eksploatacji. Powstaje pytanie: Czy wielkość przychodu np. 1 mln zł który osiągniemy w 5 roku eksploatacji danego obiektu odpowiada 1 mln zł którym dysponujemy w dniu dzisiejszym. Ilustracją tego zagadnienia jest znane przysłowie „Lepszy wróbel w garści niż gołąb na dachu". Chcąc sprowadzić wartość przychodów z przyszłych okresów do roku wyjściowego posługujemy się rachunkiem dyskontowym. Obydwie sytuacje ilustrują następujące przykłady.
Przyrost wartości pieniądza w czasie z tytułu lokaty. Dysponując kwotą np. 100 tys. zł, którą składamy w banku na okres 3 lat przy oprocentowaniu 5% w skali roku, przy corocznej kapitalizacji odsetek, czyli na tak zwany procent składany.
Wartość pieniądza (FV1) po pierwszym roku = 100 000 zł + 100 000 zł x 0,05 =
100 000 zł + 5 000 zł = 105 000 zł
Wartość pieniądza (FV2) po drugim roku = 105 000 zł + 105 000 zł x 0,05 =
105 000 zł + 5 250 zł = 110 250 zł
Wartość pieniądza (FV3) po trzecim roku = 110 250 zł +110 250 zł x 0,05=
110 250 zł+ 5 512,5 zł =115 762,5 zł
Wartość pieniądza w dowolnym roku (FVn) możemy obliczyć wg wzoru:
FVn = P(1+r)n
gdzie:
FVn - wartość pieniądza jaką uzyskamy w roku „n” po złożeniu określonej sumy pieniędzy w banku przy oprocentowaniu równym r (wyrażonym w wielkościach stosunkowych).
P - wartość pieniądza złożona na lokatę w roku początkowym.
Wartość środków po trzech latach obliczana według wzoru wynosi:
FV3 = 100 000 zł x (1 + 0,05)3 = 100 000 zł x 1,157625 = 115 762,5 zł
Podany przykład wskazuje, że w okresie 3 lat zmieniła się wartość pieniędzy złożonych na lokatę. Przyrost od złożonych 100 tys. zł. wyniósł 15762,5 zł., czyli 15,75%.
Zasada dyskonta polega na postępowaniu odwrotnym. Zakłada sprowadzenie przychodów przyszłych okresów do wartości bieżącej czyli obecnego okresu. Oblicza się ją według następujące wzoru:
gdzie:
PV - wartość bieżąca przyszłych przychodów uzyskanych w roku „N”.
Posiłkując się tym wzorem obliczamy wartość bieżącą kwoty 115 762,5 zł, którą uzyskaliśmy z lokaty 100 000 zł na koniec trzeciego roku.
Przeprowadzone obliczenie wskazuje, że wartość 115 762,5 zł, którą uzyskamy za trzy lata ma wartość realną obecnie 100 000 zł, przy przyjętej stopie dyskonta 5%.
Wartość zaktualizowana netto
Podstawową metoda oceny efektów inwestycyjnych uwzględniającą zmiany wartości pieniądza w czasie jest metoda wartości zaktualizowanej netto (NPV - Net Present Value). Zakłada ona zdyskontowanie przepływów pieniężnych z działalności operacyjnej analizowanego przedsięwzięcia inwestycyjnego. Przepływy pieniężne w roku stanowią różnicę między przychodami, a kosztami uzyskania przychodów bez uwzględniania amortyzacji. Przyjmuje się, że przedsięwzięcie jest efektywne pod warunkiem, że suma zdyskontowanych przepływów pieniężnych w okresie eksploatacji obiektu będzie wyższa od sumy poniesionych nakładów inwestycyjnych. Obliczeń dokonuje się według podanego wzoru:
gdzie:
NPV - wartość zaktualizowana netto,
FVn - przepływy pieniężne netto w kolejnych latach,
![]()
- współczynnik dyskontowy.
Metoda ta zostanie zaprezentowana na przykładzie oceny przedsięwzięcia inwestycyjnego w postaci obory na 100 stanowisk dla krów mlecznych w cyklu zamkniętym przy sprzedaży cieląt (buhajków) w wieku 2 tygodni. Przychówek żeński odchowywany jest na reprodukcję własnego stada i sprzedaż nadmiaru jałówek ciernych. Zakłada się 4 letni okres użytkowania krów (25% brakowanie) i sprzedaż 10 jałówek cielnych. Nakłady inwestycyjne łącznie z urządzeniami wewnętrznymi wyniosą 800 000 zł, co w przeliczeniu na 1 stanowisko (krowę z przychówkiem) wynosi 8000 zł. Przyjęto wydajność mleczną krów na poziomie 6500 litrów rocznie i cenie zbytu mleka 1 zł za litr. Łączne przychody oszacowano na 740 000 zł w skali roku, koszty operacyjne bez amortyzacji oszacowano na 540 000 zł, stąd wartość rocznych przepływów pieniężnych wyniesie z planowanej inwestycji 200 000 zł. Dyskontowanie przepływów należy przeprowadzić za cały okres eksploatacji obiektu, który wynosi 40 lat. W praktyce jednak nie ma potrzeby dyskontowania przepływów z całego okresu eksploatacji. Doświadczenie wskazuje, że wystarczającym okresem dyskontowania przypływów jest okres 5 lat. W tej sytuacji należy poddać dyskontowaniu również niezamortyzowaną wartość obiektu, czyli jego wartość po 5 latach eksploatacji. Wartość ta nazywana jest wartością rezydualną. Oblicza się ją jako różnice między wartością początkową a sumą odpisów amortyzacyjnych za okres 5 lat. Przyjęty 40 letni okres użytkowania obory wskazuje, że roczna rata amortyzacyjna wyniesie 20 000 zł (800 000/40 lat = 20 000). Wartość rezydualna obory po 5 latach wyniesie 700 000 zł (800 000 - 100 000 = 700 000 zł).
Kolejnym ważnym założeniem jest przyjęcie stopy dyskonta. Poziom stopy dyskonta zależy od dwóch elementów. Pierwszy odpowiadający oprocentowaniu długoterminowych wkładów bankowych, który obecnie możemy przyjąć na poziomie 5%. Drugi element wyrażony w procentach stanowi cenę ryzyka związanego z danym przedsięwzięciem, jego poziom ustala sam inwestor. Im większe ryzyko, tym większa powinna być wartość tej części stopy dyskonta. W tym przykładzie cenę ryzyka przyjmujemy umownie na poziomie 5% zatem przyjęta stopa dyskonta wynosić będzie 10%. Przykład obliczenia wartości zaktualizowanej netto przedstawiono w tabeli 1.
Tabela 1. Obliczenie wartości zaktualizowanej netto
Rok |
Przepływy pieniężne (zł) |
Współczynnik dyskonta (10%) |
NPV (zł) |
0 |
- 800 000 |
1 |
-800 000 |
1 |
200 000 |
0,9090 |
181 800 |
2 |
200 000 |
0,8264 |
165 280 |
3 |
200 000 |
0,7513 |
150 260 |
4 |
200 000 |
0,6830 |
136 660 |
5 |
200 000 |
0,6209 |
124 180 |
|
700 000 (wartość rezydualna) |
0,6209 |
434 630 |
|
Razem |
X |
392 750 |
Zgodnie z metodą nakłady inwestycyjne poniesione w roku wyjściowym ujmowane są ze znakiem „minus” i nie podlegają dyskontowaniu. W sytuacji, gdy proces inwestowania trwa dłużej, nakłady inwestycyjne w kolejnych latach występują także ze znakiem „minus" i podlegają dyskontowaniu. Wyniki obliczeń przedstawione w tabeli 1 wskazują, że dana inwestycja przy założonych warunkach jest ekonomicznie uzasadniona. Aby w pełni potwierdzić ten fakt należy obliczyć również wewnętrzną stopę zwrotu (IRR - Internal Rate of Return).
Jeśli otrzymana wartość netto (NPV) jest dodatnia, to stopa rentowności inwestycji jest wyższa niż minimalna stopa graniczna. Projekt o wartości NP. dodatniej bądź zerowej można uznać za możliwy do przyjęcia. W przypadku ujemnej wartości NP. stopa rentowności projektu jest niższa niż stopa graniczna, projekt przedsięwzięcia powinien być odrzucony. Jeśli dokonuje się wyboru jednego lub z kilku projektów alternatywnych, to trzeba wybrać ten, dla którego wartość zaktualizowana netto jest najwyższa (spośród NPV≥0)
Wewnętrzna stopa zwrotu
Wewnętrzna stopa zwrotu (IRR) to stopa dyskonta, przy której wartość zaktualizowana netto ocenianego przedsięwzięcia jest równa 0 (NPV = 0). IRR oblicza się według następującego wzoru:
gdzie:
r1 - poziom stopy procentowej, przy którym NPV>0,
r2 - poziom stopy procentowej, przy której NPV<0,
PV - zaktualizowana wartość netto (dodatnia) dla niskiej stopy dyskontowej r1,
NV - zaktualizowana wartość netto (ujemna) dla wysokiej stopy dyskontowej r2.
Obliczenia IRR przeprowadza się w kilku etapach prowadzących do obliczeń NPV > 0 i NPV < 0. Wymaga to założenia wartości r1, przy której NPV będzie dodatnie, ale blisko wartości 0 i r2, przy którym NPV będzie ujemne. Obliczenia przedstawiono w kolejnych tabelach 2 i 3 gdzie przyjęto stopę dyskonta r1=20%, r2 = 25%.
Tabela 2. Obliczenie wartości zaktualizowanej netto przy r1=20%
Rok |
Przepływy pieniężne (zł) |
Współczynnik dyskonta (20%) |
NPV (zł) |
0 |
- 800 000 |
1 |
-800 000 |
1 |
200 000 |
0,8330 |
166 600 |
2 |
200 000 |
0,6944 |
138 880 |
3 |
200 000 |
0,5787 |
115 740 |
4 |
200 000 |
0,4822 |
96 440 |
5 |
200 000 |
0,4018 |
80 360 |
|
700 000 (wartość rezydualna) |
0,4018 |
281 260 |
|
Razem |
|
79 280 |
Tabela 3. Obliczenie wartości zaktualizowanej netto przy r2 = 25% |
|||
Rok |
Przepływy pieniężne (zł) |
Współczynnik dyskonta (25%) |
NPV (zł) |
0 |
- 800 000 |
1 |
-800 000 |
1 |
200 000 |
0,8000 |
160 000 |
2 |
200 000 |
0,6400 |
128 000 |
3 |
200 000 |
0,5120 |
102 401 |
4 |
200 000 |
0,4096 |
81920 |
5 |
200 000 |
0,3276 |
65 537 |
|
700 000 (wartość rezydualna) |
0,3276 |
229 376 |
|
Razem |
|
-32 766 |
W oparciu o uzyskane wyniki obliczamy IRR:
Obliczona wartość IRR wskazuje, że graniczna stopa dyskonta wynosi 23,538% i znacznie przewyższa wartość przyjętej stopy dyskonta na poziomie 10%. Wynik ten wskazuje nie tylko na ekonomicznie uzasadnioną decyzję inwestycyjną lecz także na wysoki poziom bezpieczeństwa. Im większa różnica między wartością IRR, a przyjęta stopą dyskonta tym wyższy poziom bezpieczeństwa danej inwestycji.
Wewnętrzną stopę zwrotu można również wyznaczyć metodą graficzną w następujący sposób:
na osi odciętych zaznaczyć poziom stóp dyskontowych (procentowych) r1 i r2, dla których przeprowadzono obliczenia NPV,
no osi rzędnych zaznaczyć obliczoną dodatnią PV i ujemną NV wartość zaktualizowaną netto,
wykreślić linię łączącą punkty (r1, PV) i (r2, NV); linia ta przetnie oś odciętych w punkcie, w którym stopa dyskontowa równa się wewnętrznej stopie zwrotu danego przedsięwzięcia (rys. 2)
Rys.2. Wyznaczenie IRR w sposób graficzny
NPV
![]()
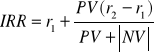
![]()
![]()
![]()
Popyt inwestycyjny
I0
I1
r0
Stopa procentowa
r1
PV
NV
r1
r2
Stopa dyskontowa
IRR
Wyszukiwarka