PODSTAWY KONSTRUKCJI MASZYN

Projekt wału maszynowego dwupodporowego

Projekt wykonał: Maciej Rudolf

Grupa T-32

Wydział Inżynierii Materiałowej Metalurgii i Transportu

Kierunek Transport

Katowice 2000

Dane Obliczenia i szkice Wyniki

Temat: Zaprojektować wał maszynowy dwupodporowy według schemat podanego

rysunku. W punkcie 1 osadzone jest koło napędzające przekładnię zębatą o zębach

skośnych, w punkcie 2 - koło pasowe przekładni pasowej klinowej odbierającej

moc z wału. W punktach podparcia wału A i B znajdują się łożyska kulkowe to-

czne. Do obliczeń przyjąć następujące dane:

N=40 kW

n=1500 obr/min

l=0,9 m.

a=b=c=1/3*l

materiał: stal węglowa zwykłej jakości ST5

A B

1 2

a b c

l

N=100%

40%

100%

N=40 kW

n=1500 obr/min

l=0,9 m.

a=b=c=0,3 m.

1 Dobieram materiał na wał i określam podstawowe parametry wytrzymałościowe

Na postawie norm na wykonanie wału wybieram stal węglową St5 której parametry

wytrzymałościowe są następujące:

k_go=60 Mpa, k_sj=69 Mpa

Dane Obliczenia i szkice Wyniki

1. Przedstawienie schematu rozkładu wszystkich sił działających na wał z

odpowiednimi reakcjami działającymi w miejscu osadzenia. Zaniedbuję ciężar

kół oraz wału maszynowego.

Rby

Rbx

Qz

Pa

Ray Q Qx Rbz

Pr P

Po

Raz Qx

Qz

2 Obliczenie wszystkich sił występujących w kołach zębatych o zębach skośnych.

W kole zębatym występują 3 siły: Po, Pa i Pr. Obliczam wartość momentu skręca-

jącego dla koła zębatego:

N=40 kW

n=1500

Obr/min
Nm Ms=254,66Nm

Obliczam średnicę podziałową koła przyjmując moduł m=0,012 m. m.=0,012m

Teoretyczna graniczna liczba zębów z_g dla kąta przyporu α_o=20° wynosi:

α_o=20°

z_g=17

Przy z<z_g występuje podcięcie stopy zęba u podstawy. Ponieważ w praktyce

dopuszcza się nieznaczne podcięcie nie powodujące ujemnych skutków wprowa-

dza się praktyczną graniczną liczbę zębów z_g', określoną wzorem:

z_g=17
z_g'=14

Dane Obliczenia i szkice Wyniki

Przyjmuję liczbę zębów koła zębatego równą: z₁=19 z₁=19

Obliczam wymiary charakteryzujące ząb:

• wysokość głowy zęba:

m.=0,012m.
h_a=0,012m

• wysokość stopy zęba:

h_f=0,014m

• wysokość całkowitą zęba:

h=0,0264m

Wyznaczam średnicę podziałową ze wzoru:

m.=0,012m.

β=10°
d_o=0,231m.

z₁=19

Obliczam średnicę wierzchołków zębów:

d_o=0,231m.
d_a1=0,255m

h_a=0,012m.

Obliczam średnicę podstaw zębów:

d_o=0,231m.
d_f1=0,2027m.

h_f=0,0144m

Obliczam wartość podziałki:

d_o=0,231m.
p₁=0,0383m.

z₁=19

Obliczenia dla drugiego koła zębatego (współpracującego):

Przyjmuję liczbę zębów z₂=25

Wyznaczam średnicę podziałową ze wzoru:

m.=0,012m.

z₂=25
d_o2=0,304m.

β=10°

Obliczam średnicę wierzchołków zębów:

d_o2=0,304m.
d_a2=0,328m

h_a=0,012m.

Obliczam średnicę podstaw zębów:

Dane Obliczenia i szkice Wyniki

d_o2=0,3046m.
d_f2=0,2758m.

h_f=0,0144m

Obliczam podziałkę:

d_o2=0,3046m.
p₂=0,0383m.

z₂=25

Obliczam szerokości zębów:

p₁=0,0383m.

s=0,0188m

Obliczam szerokość wrębu:

p₁=0,0383m.
e=0,0195m.

Obliczam luz obwodowy zazębienia:

e=0,0195m.

s=0,0188m.
j_t=0,0007

Odległość osi kól zębatych wynosi:

d_o1=0,231m.
a=0,268m.

d_o2=0,3046m.

Wartość przełożenia wynosi:

z₁=19

z₂=25

u >1 więc przekładnia ta jest reduktorem.

2.1 Obliczenie siły obwodowej Po

Ms=254,66Nm

d_o1=0,231m.
P_o=2200N

2.2 Obliczenie siły promieniowej Pr

α_wn=20°

β=10° α_wn- to kąt przyporu na średnicy tocznej w przekroju normalnym. Przyjmuję

P_o=2200N α_wn=20°

P_r=813,07N

Dane Obliczenia i szkice Wyniki

1. Obliczenie siły osiowej

P_o=2200N

β=10°
P_a=387,91N

3 Określenie sił i zależności geometrycznych w przekładni pasowej.

γ - kąt rozwarcia cięgien

α - kąt opasania

S₁ - naciąg czynny

S₂ - naciąg bierny

S₂

S₂

α

D₁ D₂

Q

S₁

α S₁

2

a

Y

α=180°-γ

S₂

Q_x x

γ

Q_y Q

S₁

Dane Obliczenia i szkice Wyniki

3.1 Z tablic dobieram znormalizowaną średnicę koła pasowego D₁=0,2m.

Jeżeli przełożenie przekładni wynosi 2 to możemy wyliczyć średnicę drugiego

koła:

D₁=0,2m.

D₂=0,4m.

3.2 Obliczenie odległości między kołami przekładni pasowej.

Minimalną odległość między osiami kół obliczam z następującej zależności:

D₁=0,2m.

D₂=0,4m.
a_min=0,35m.

Maksymalna odległość między osiami kół wynosi:

D₁=0,2m.

D₂=0,4m.
a_max=1,2m.

zatem dla danej przekładni pasowej przyjmuję odległość

między osiami kół równą a=0,6m. a=0,6m.

3.3 Obliczam kąt opasania na kole czynnym.

D₁=0,2m.

a=0,6m
ale
i

D₁=średnica czynnego koła pasowego

α=160,81°=

=2,8 rad

3.4 Obliczam kąt rozwarcia cięgien

α=2,8 rad

γ=19,18°=

=0,34 rad

3.5 Obliczam siłę obwodową dla przekładni pasowej

Obliczam moment skręcający na kole pasowym, a ponieważ oddaje ono 60% mocy

dostarczonej, dlatego:

N=40 kW

N=1500obr/m.
N₁=16kW

D₁=0,2m.

Ms=101,86Nm

P_o=1018,7N

Dane Obliczenia i szkice Wyniki

3.6 Obliczam napięcia cięgien ze wzoru Eulera

Obliczam prędkość pasa

D₁=0,2m.

N=1500
V=15,7m/s

obr/min

Obliczam rzeczywisty współczynnik tarcia:

V=15,7m/s

μ=0,457

Obliczam pozorny współczynnik tarcia, gdzie β to kąt zarysu rowka na kole

Czynnym wynoszący β=40°.

μ=0,457

β=40°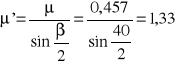
μ'=1,33

stąd ze wzoru Eulera:

μ'=1,33

α=2,82 rad
m.=42,6

Napięcia cięgien wynoszą:

P_o=1018,7N

m.=42,6
S₁=1043,1N

S₂=24,45N

3.7 Obliczam siłę wypadkową Q napięć w cięgnach i jej składowe:

S₁=1043,1N

S₂=24,45N

α=160,81°
Q=1066,2N

Obliczam kąt pochylenia wypadkowej Q:

m.=42,6

gdzie

υ=9,16°=

=0,1599 rad

Obliczam stopień wykorzystania pasa:

Dane Obliczenia i szkice Wyniki

S₁=1043,1N

S₂=24,45N
ϕ=0,95

Obliczam wartości składowych wypadkowej Q napięć w cięgnach:

υ=9,16°

Q=1066,2N
Q_x=1052,6N

Q_y=169,77N

3.8 Obliczam przełożenie przekładni

D₁=0,2m.

D₂=0,4m.
i_r=0,5

3.9 Dobieram odpowiednie współczynniki i na ich podstawie obliczam długość

pasa i liczbę pasów przekładni pasowej

Dobieram współczynnik przełożenia przekładni c_i zależny od przełożenia: c_i=1,15 c_i=1,15

Dobieram współczynnik trwałości pasa: c_t=1,2 c_t=1,2

Obliczam średnicę równoważną potrzebną do określenia typu pasa i mocy przez

niego przenoszonej:

D₁=0,2m.

c_i=1,15
D_e=0,23

Obliczam kąt opasania większego koła pasowego:

γ=19,18°=

=0,34rad
ϕ=199,18°

Na podstawie tablic odczytuję wartość współczynnika zależnego od kąta opasania ϕ

c_ϕ=0,95 c_ϕ=0,95

Na podstawie V i D_e odczytuję z tablic moc przenoszoną przez jeden pas klinowy

N₂=9,5 KM czyli
N₂=6,992kW

Jest to pas typu C.

Długość pasa przekładni pasowej otwartej wynosi:

D₁=0,2m.

D₂=0,4m.

γ=19,18°
L=2,159m

a=0,6m.

Dane Obliczenia i szkice Wyniki

Obliczam liczbę pasów potrzebnych do przenoszenia wcześniej wyliczonej mocy

Dobieram współczynnik c_l=0,89 zależny od typu i długości pasa

c_l=0,89

c_ϕ=0,95

N₂=6,992kW

N=40kW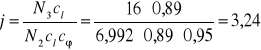
j=3,24

Przyjmuję liczbę pasów przekładni równą 4.

4. Obliczenia sił i reakcji w podporach wału maszynowego

Schemat kinematyczny wału wraz z podaniem rozkładu sił i występujących reakcji

w dwóch płaszczyznach X-Y oraz X-Z

x

z

y C Pa

Pr dw1

• Qx

A B Rbx

Ray Rby

x

z

Po Qz

A B

Raz Rbz

4.1 Określam reakcje występujące w układzie X-Y

Dane Obliczenia i szkice Wyniki

Pa=387,91N

Pr=813,08N

Qx=1052,6N
Rbx=387,91N

dw=d_o=0,231m.

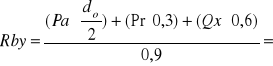
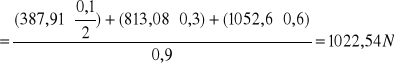
Rby=1022,54N

Ray=843,13N

4.2 Określam reakcje występujące w układzie X-Z

Po=2200N

Qz=169,77N

Rbz=620,15N

Raz=1410,08N

5 Określam momentów zginających występujących na wale

Pa=387,91N 5.1 Wyznaczam momenty zginające w płaszczyźnie X-Y

Pr=813,08N

Po=2200N przedział

Qz=169,77N

Qx=1052,6N

Rbx=387,91N

Rby=1022,54N
Mg(0)=0

Ray=843,13N

Rbz=620,15N
Mg(0,3)=

Raz=1410,08N =-252,94Nm

dw=d_o=0,231m

Dane Obliczenia i szkice Wyniki

przedział

Mg(0,3)=
=-297,74Nm

Mg(0,6)=

=-306,76Nm

przedział

Mg(0,6)=

=-306,76Nm

Dane Obliczenia i szkice Wyniki

Mg(0,9)=0Nm

5.1 Wyznaczam momenty zginające w płaszczyźnie X-Z

Raz=1410,08N

Po=2200N przedział

Qz=169,77N

Mg(0)=0Nm

Mg(0,3)=

=-423,02Nm

przedział

Mg(0,3)=

=-423,02Nm

Dane Obliczenia i szkice Wyniki

Mg(0,6)=

=-186,046Nm

przedział

Mg(0,9)=0Nm

5.2 Określam moment gnący zastępczy

Dzielę wał na 9 przekrojów, w taki sposób, aby można było wyodrębnić na

jego długości 10 przedziałów. Jeżeli doliczymy do tego dwa przekroje na końcach

wału to otrzymamy 13 przekrojów w których obliczamy moment gnący zastępczy

Dane Obliczenia i szkice Wyniki

Mg=0Nm

Mg=-75,88Nm
Mg₁=0Nm Mg=-151,76Nm

Mg=-227,64Nm
Mg₂=147,86Nm

Mg=-252,94Nm

Mg=-297,74Nm
Mg₃=295,72Nm

Mg=-299,54Nm

Mg=-302,25Nm
Mg₄=443,58Nm

Mg=-304,95Nm

Mg=-306,76Nm
Nm na kole zębatym Mg₅=492,87Nm

Mg=-276,08Nm
na kole zębatym Mg₆=517,3Nm

Mg=-184,05Nm

Mg=-92,028Nm
Nm Mg₇=480,44Nm

Mg=0Nm

Mg=0Nm
Mg₈=429,06Nm

Mg=-126,91Nm

Mg=-253,81Nm
Mg₉=384,05Nm

Mg=-380,7Nm
na kole pasowym Mg₁₀=358,77Nm

Mg=-423,02Nm

Mg=-423,02Nm
Nm Mg₁₁=322,89Nm

Mg=-375,62Nm

Mg=-304,53Nm
Nm Mg₁₂=215,26Nm

Mg=-233,44Nm

Mg=-186,04Nm
Mg₁₃=107,63Nm

Mg=-167,44Nm

Mg=-111,62Nm
Nm Mg₁₄=0Nm

Mg=-55,81Nm

Mg=0Nm

5.3 Obliczam moment skręcający występujący wzdłuż wału

N=40 kW

N- moc przenoszona przez wał, kW

n - prędkość obrotowa, obr/min

Nm Ms₁=254,66Nm

Ms₂=254,66Nm

Dane Obliczenia i szkice Wyniki

Ms₃=254,66Nm

Ms₄=254,66Nm

Ms₅=254,66Nm

Ms₆=254,66Nm

Ms₇=101,86Nm

Ms₈=101,86Nm

Ms₉=101,86Nm

Ms₁₀=101,86Nm

Ms₁₁=0Nm

Ms₁₂=0Nm

Ms₁₃=0Nm

Ms₁₄=0Nm

5.4 Obliczam moment skręcający Ms'

Ms₁=254,6Nm

Ms₂=254,6Nm
Ms₁'=169,77Nm

Ms₃=254,6Nm

Ms₄=254,6Nm
Ms₂'=169,77Nm

Ms₅=254,6Nm

Ms₆=254,6Nm
Ms₃'=169,77Nm

Ms₇=101,8Nm

Dane Obliczenia i szkice Wyniki

Ms₈=101,8Nm
Ms₄'=169,77Nm

Ms₉=101,8Nm

Ms₁₀=101,8Nm
Ms₅'=169,77Nm

Ms₁₁=0Nm
Ms₆'=169,77Nm

Ms₁₂=0Nm

Ms₁₃=0Nm
Ms₇'=67,91Nm

Ms₁₄=0Nm

Ms₈'=67,91Nm

Ms₉'=67,91Nm

Ms₁₀'=67,91Nm

Ms₁₁'=0Nm

Ms₁₂'=0Nm

Ms₁₃'=0Nm

Ms₁₄'=0Nm

5.5 Obliczam moment zastępczy Mz

Mg₁=0Nm

Mg₂=147,86Nm

Mg₃=295,72Nm

Mg₄=443,58Nm
Mz₁=254,66Nm Mg₅=492,87Nm

Mg₆=517,3Nm
Mz₂=225,14Nm

Mg₇=480,44Nm

Mg₈=429,06Nm
Mz₃=340,99Nm

Mg₉=384,05Nm

Mg₁₀=358,77Nm
Mz₄=474,96Nm

Mg₁₁=322,89Nm

Dane Obliczenia i szkice Wyniki

Mg₁₂=215,26Nm
Mz₅=521,29Nm

Mg₁₃=107,63Nm

Mg₁₄=0Nm
Mz₆=544,44Nm

Ms₁'=169,77Nm

Ms₂'=169,77Nm
Mz₇=485,22Nm

Ms₃'=169,77Nm

Ms₄'=169,77Nm
Mz₈=434,40Nm

Ms₅'=169,77Nm

Ms₆'=169,77Nm
Mz₉=390,01Nm

Ms₇'=67,91Nm

Ms₈'=67,91Nm
Mz₁₀=365,14Nm

Ms₉'=67,91Nm

Ms₁₀'=67,91Nm
Mz₁₁=322,89Nm

Ms₁₁'=0Nm

Ms₁₂'=0Nm
Mz₁₂=215,26Nm

Ms₁₃'=0Nm

Ms₁₄'=0Nm
Mz₁₃=107,63Nm

Mz₁₄=0Nm

6 Wyznaczam średnice wału w 10 przekrojach i na ich podstawie wykreślam

Ms₁=254,6Nm paraboloidę obrotową będącą teoretycznym zarysem wałka

Mz₂=225,13Nm

Mz₃=340,99Nm W przypadku, gdy moment gnący wypadkowy jest równy 0 Mg(w)=0, to średnicę

Mz₄=474,96Nm wyliczamy z następującego wzoru wytrzymałościowego, mamy do czynienia tylko

Mz₅=521,29Nm ze skręcaniem:

Mz₆=544,44Nm

Mz₇=485,21Nm

Mz₈=434,40Nm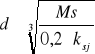

Mz₉=390,01Nm

Mz₁₀=365,14Nm

Mz₁₁=322,89Nm W przypadku gdy moment gnący jest wartością większą od 0 (występuje zarówno

Mz₁₂=215,26Nm skręcanie i zginanie to średnice wyliczamy następująco:

Mz₁₃=107,63Nm

Mz₁₄=0Nm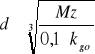

k_sj=69Mpa

k_go=60MPa Średnice wynoszą:

Ms=254,66Nm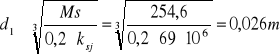
d₁=0,026m.

Dane Obliczenia i szkice Wyniki

Mz₂=340Nm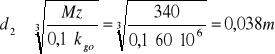
d₂=0,038m

Mz₃=425Nm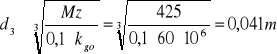
d₃=0,041m.

Mz₄=510Nm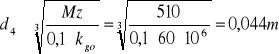
d₄=0,044m.

Mz₅=521,29Nm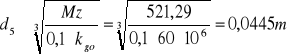
d₅=0,0445m.

Mz₆=544,44Nm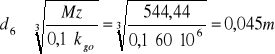
d₆=0,045m.

Mz₇=485,21Nm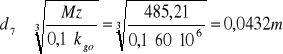
d₇=0,0432m.

Mz₈=434,4Nm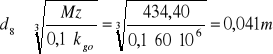
d₈=0,041m.

Mz₉=390,01Nm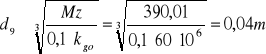
d₉=0,04m.

Mz₁₀=365,14Nm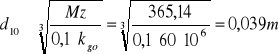
d₁₀=0,039m.

Za kołem pasowym występuje już tylko zginanie, dlatego do obliczeń wykorzystu-

jemy tylko odpowiednie momenty gnące wypadkowe:

Mg(w)=322,9Nm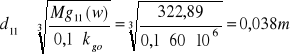
d₁₁=0,038m.

Mg(w)=215,26Nm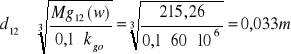
d₁₂=0,033m.

Mg(w)=107,63Nm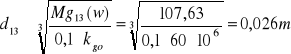
d₁₃=0,026m.

d₁₄=0m.

Dane Obliczenia i szkice Wyniki

Na wykreślony teoretyczny zarys wału (parabooidę) nanoszę rzeczywisty kształt

wału uwzględniając znormalizowane średnice czopów pod wszystkie elementy

na nim osadzone.

• Określam maksymalną strzałkę ugięcia wału.

1. Obliczam ilorazy momentów gnących wypadkowych przez momenty bezwład-

ności przekrojów (czyli określam tzw. moment fikcyjny).

Mg₁=0Nm

Mg₂=147,86Nm

Mg₃=295,72Nm

Mg₄=443,58Nm

Mg₅=492,87Nm Mg(w) - moment gnący wypadkowy

Mg₆=517,3Nm d - średnica wału

Mg₇=480,44Nm I - moment bezwładności przekroju

Mg₈=429,06Nm

Mg₉=384,05Nm
Mf1=0N/m3

Mg₁₀=358,77Nm

Mg₁₁=322,89Nm
Mf1=4,3*10^8N/_m³

Mg₁₂=215,26Nm

Mg₁₃=107,63Nm
Mf2a=1,7*10^8N/_m³

Mg₁₄=0Nm

d₁=0,026m.
Mf3=4,5*10^8N/_m³

d₂=0,033m.

d₃=0,038m.
Mf3a=2,2*10^8N/_m³

d₄=0,043m.

d₅=0,044m.
Mf4=4,0*10^8N/_m³

d₆=0,045m.

d₇=0,0432m.
Mf4a=2,2*10^8N/_m³

d₈=0,041m.

d₉=0,04m.
Mf5=3,0*10^8N/_m³

d₁₀=0,039m.

d₁₁=0,037m.
Mf5a=1,7*10^8N/_m³

d₁₂=0,032m.

d₁₃=0,026m.
Mf6=2,5*10^8N/_m³

d₁₄=0m.

Dane Obliczenia i szkice Wyniki

Mf6a=2,5*10^8N/_m³

Mf7=2,3*10^8N/_m³

Mf7a=1,4*10^8N/_m³

Mf8=1,3*10^8N/_m³

Mf8a=0,8*10^8N/_m³

Mf9=0,8*10^8N/_m³

Mf9a=1,3*10^8N/_m³

Mf10=1,1*10^8N/_m³

Mf10a=1,9*10^8N/_m³

Mf11=1,7*10^8N/_m³

Mf11a=1,7*10^8N/_m³

Mf12=1,3*10^8N/_m³

Mf12a=2,2*10^8N/_m³

Mf13=1,6*10^8N/_m³

Mf13a=3,0*10^8N/_m³

Dane Obliczenia i szkice Wyniki

Mf14=1,9*10^8N/_m³

Mf14a=4,0*10^8N/_m³

Mf15=1,7*10^8N/_m³

Mf15a=4,3*10^8N/_m³

Na podstawie uzyskanych wyników sporządziłem tzw. „wykres piły”, który

przedstawiony jest wraz z innymi wykresami na papierze milimetrowym.

2. Obliczam pola trójkątów i trapezów otrzymanych na wykresie piły.

Długości podstaw tych figur stanowią obliczone wcześniej momenty fikcyjne.

h₁=0,04m

h₂=0,06m

h₃=0,08m
S₁=8,75*10^6N/m²

h₄=0,07m

h₅=0,05m.
S₂=19,0*10^6N/m²

h₆=0,07m

h₇=0,08m.
S₃=25,1*10^6N/m²

h₈=0,02m

h₉=0,07m.
S₄=18,4*10^6N/m²

h₁₀=0,135m

h₁₁=0,06m.
S₅=10,9*10^6N/m²

h₁₂=0,06m

h₁₃=0,065m.
S₆=14,2*10^6N/m²

h₁₄=0,04m

Mf₂=4,3*10⁸N/m³
S₇=13,0*10^6N/m²

Mf_2a=1,7*10⁸N/m³

Mf₃=4,5*10⁸N/m³
S₈=2,19*10^6N/m²

Mf_3a=2,2*10⁸N/m³

Mf₄=4,0*10⁸N/m³
S₉=8,73*10^6N/m²

Dane Obliczenia i szkice Wyniki

Mf_4a=2,2*10⁸N/m³

Mf₅=3,0*10⁸N/m³
S₁₀=21,9*10^6N/m²

Mf_5a=1,7*10⁸N/m³

Mf₆=2,5*10⁸N/m³
S₁₁=11,8*10^6N/m²

Mf_6a=2,5*10⁸N/m³

Mf₇=2,3*10⁸N/m³
S₁₂=15,0*10^6N/m²

Mf_7a=1,4*10⁸N/m³

Mf₈=1,3*10⁸N/m³
S₁₃=19,0*10^6N/m²

Mf_8a=0,8*10⁸N/m³

Mf₉=0,8*10⁸N/m³
S₁₄=8,75*10^6N/m²

Mf_9a=1,3*10⁸N/m³

Mf₁₀=1,1*10⁸N/m³ Wektory S równe polom trapezów i trójkątów umieszczam w ich środkach

Mf_10a=1,9*10⁸N/m³ ciężkości.

Mf₁₁=1,7*10⁸N/m³

7.3 Obliczam środki ciężkości wszystkich otrzymanych figur.

Mf_11a=1,7*10⁸N/m³

Mf₁₂=1,3*10⁸N/m³
z₁=0,026m

Mf_12a=2,2*10⁸N/m³

Mf₁₃=1,6*10⁸N/m³
gdzie: h- długość czopu

Mf_13a=3,0*10⁸N/m³ c - dłuższa podstawa trapezu (Mf)

Mf₁₄=1,9*10⁸N/m³ b - krótsza podstawa trapezu (Mf tego samego

Mf_14a=4,0*10⁸N/m³ przekroju)

Mf₁₅=1,7*10⁸N/m³

Mf_15a=4,3*10⁸N/m³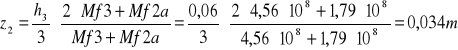
z₂=0,034m

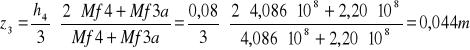
z₃=0,044m

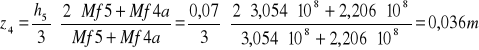
z₄=0,036m

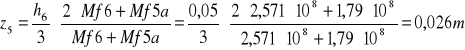
z₅=0,026m

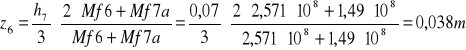
z₆=0,038m.

Dane Obliczenia i szkice Wyniki

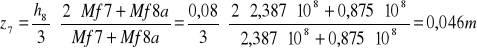
z₇=0,046m

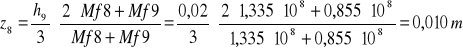
z₈=0,010m

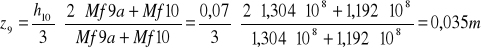
z₉=0,035m

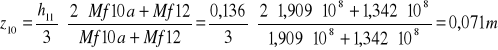
z₁₀=0,071m

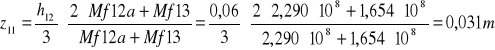
z₁₁=0,031m

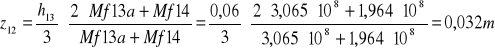
z₁₂=0,032m

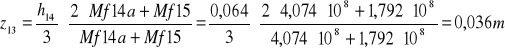
z₁₃=0,036m

z₁₄=0,026m.

Po zilustrowaniu wykresu piły wraz z wektorami S umieszczonymi w środkach

ciężkości figur, wykreślam na oddzielnym wykresie

metodą wieloboku sznurowego.

3. Obliczam maksymalną strzałkę ugięcia wału.

κ_s=10⁶

N/(m²/mm) κ_s - to podziałka w której były liczone pola trójkątów i trapezów

κ_l=5(mm/mm) κ_l - to podziałka w której został zrobiony wykres wieloboku sznurowego

H=100mm H - długość osi biegunowej

E=2,1⋅10⁵⋅10⁶

N/m²

κ_f=0,002

mm/mm

Z wykresu otrzymujemy najdłuższą odległość y_f=38mm i podstawiamy do wzoru:

f=0,09mm

Otrzymaną wartość porównujemy z wartością dopuszczalną, którą obliczamy

Wykorzystując wartość długości wału:

Dane Obliczenia i szkice Wyniki

f_dop=0,27mm

0,09mm < 0,27mm

zatem warunek jest spełniony.

• Dobór łożysk

1. Dobór i obliczenie współczynników f_t, f_h, f_n

Przyjmuję współczynnik temperatury f_t=0,9 dla łożysk pracujących w temperaturze

powyżej 100°C. f_t=0,9

Obliczam współczynnik trwałości, przyjmując liczbę godzin pracy łożyska =10000

L_h=10000
f_h=2,714

Obliczam współczynnik obrotów:

N=1500

obr/min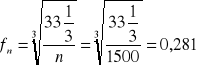
f_n=0,281

2. Obliczam siły wzdłużne Fw i poprzeczne Fp działające na łożyska

Dla podparcia w punkcie A:

Ray=843,13N

Raz=1410,08N
Fp_a=1643N

=0 brak siły osiowej w punkcie A Fw_a=0

Przyjmuję, że zastosowanym łożyskiem będzie łożysko kulkowe zwykłe

Obliczam stosunek siły wzdłużnej do poprzecznej w punkcie A

Fp_a=1643N

Fw_a=0
ponieważ stosunek ten jest mniejszy od wartości e odczytanej

z tabeli przyjmuję więc parametry: Xa=1, Ya=0 oraz V=1,

ponieważ to wałek się obraca, zatem obciążenie zastępcze wyn.:

Fa=1643N

Obliczam nośność ruchową łożyska

Fa=1643N

f_t=0,9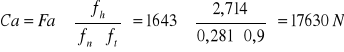
Ca=17630N

Dane Obliczenia i szkice Wyniki

f_h=2,714

f_n=0,281

Dla podparcia w punkcie B:

Rby=1022,54N

Rbz=620,15N
Fp_b=1196N

Rbx=387,91N

Fw_b=387,91

Obliczam stosunek siły wzdłużnej do poprzecznej w punkcie B

Fp_b=1196N

Fw_b=387,91
ponieważ stosunek ten jest większy od wartości e odczytanej

z tabeli przyjmuję więc parametry: Xb=0,56, Ya=1,45 oraz V=1,

ponieważ to wałek się obraca, zatem obciążenie zastępcze wyn.:

Fb=1232N

Obliczam nośność ruchową łożyska

Fb=1232N

f_t=0,9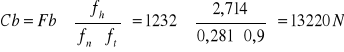
Cb=13220N

f_n=0,281

f_h=2,714

Z katalogu łożysk, biorąc pod uwagę otrzymane wartości nośności dobieram

następujące łożyska :

Dla punktu A i B dobieram łożysko kulkowe zwykłe typu 6208 o wymiarach :

d=40mm, D=80mm, B=18mm

• Obliczenie zmęczeniowego współczynnika bezpieczeństwa wybranego przekroju

1. Dla obustronnie zmiennego cyklu zginania wału naprężenie średnie σ_mg=0, a

Amplituda naprężeń wynosi :

d=80mm

Mg_kz=544,5Nm
σ_ag=10,83MPa

Ms=254,66Nm

τ_m.=1,267Mpa

Z tablic wypisuję własności wytrzymałościowe stali St5:

R_r=550Mpa, Qg=370Mpa Qs=180Mpa

Zgo=240Mpa Zso=130Mpa

Zgj=420Mpa Zsj=280Mpa

Dane Obliczenia i szkice Wyniki

Z wykresu zawartego w książce odczytuję dla stali St5 minimalny promień zaokrą-

gleń:

ρ_m.=0,65mm

ρ_k=3mm

ρ=ρ_m.+ ρ_k=0,65+3=3,65mm ρ=3,65mm

Obliczam stosunki średnic czopów w badanym przekroju, na których opiera się

koło zębate

D=90mm

d=80mm

D/d=1,12

ρ/d=0,046

Dla obliczonych powyżej stosunków odczytujemy wartości współczynników

kształtu

współczynnik kształtu dla zginania: α_kg=1,8 α_kg=1,8

współczynnik kształtu dla skręcania: α_ks=1,45 α_ks=1,45

współczynnik wrażliwości: η=1,8 η=1,8

współczynnik stanu powierzchni dla zginania: β_p=1,06 β_p=1,06

współczynnik stanu powierzchni dla skręcania: β_ps=1,03 β_ps=1,03

2. Obliczam współczynniki spiętrzenia naprężeń

α_kg=1,8

α_ks=1,45
β_g=1,56

η=1,8

β_p=1,06
β_s=1,303

β_ps=1,03

Z tabel odczytuję wskaźniki wielkości przedmiotu:

α_kg=1,86 γ_g=1,48 α_kg=1,86

α_ks=1,5 γ_s=1,39 γ_g=1,48

α_ks=1,5

γ_s=1,39

9.3 Obliczam zmęczeniowy współczynnik bezpieczeństwa z uwzględnieniem tylko

zginania

β_g=1,56

γ_g=1,48

σ_ag=10,83Mpa
Xzg=9,594

Zgo=240Mpa

Zsj=280Mpa Obliczam zmęczeniowy współczynnik bezpieczeństwa z uwzględnieniem tylko

skręcania

Zso=130Mpa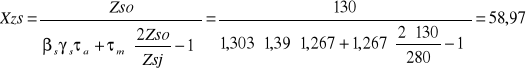
Xzs=58,97

Dane Obliczenia i szkice Wyniki

γ_s=1,39 Zmęczeniowy współczynnik bezpieczeństwa obliczanego wału ma wartość:

β_s=1,303

τ_m.=1,267Mpa

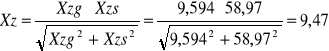
Xz=9,47

3. Obliczam wymagany współczynnik bezpieczeństwa:

X₁=1,2

X₂=1,1
Xzw=1,32

X₃=1

X₄=1 1,32 < 9,47 a więc warunek został spełniony.

---