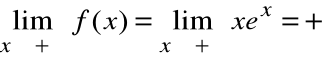Badanie funkcji
1. Monotoniczność funkcji
R - zbiór liczb rzeczywistych
Definicje
Funkcja f(x) rosnąca lub malejąca na zbiorze A nazywa się funkcją monotoniczną na A.
Funkcja f(x) ściśle rosnąca lub ściśle malejąca na zbiorze A nazywa się funkcją ściśle monotoniczną na A.
Twierdzenie (warunek wystarczający)
Jeżeli f′ (x) > 0 dla każdego x ∈ (a,b), to funkcja f(x) jest ściśle rosnąca w tym przedziale.
Jeżeli f′ (x) < 0 dla każdego x ∈ (a,b), to funkcja f(x) jest ściśle malejąca w tym przedziale.
Przykład
f(x) = x3+3x2-7
f′ (x) =3x2 +6x =3x(x+2)
f′ (x) =0 dla x=0 lub x=-2
f′ (x) > 0 dla x ∈ (-∞, -2) ∪ (0, +∞) -
funkcja jest ściśle rosnąca
f′ (x) < 0 dla x ∈ (-2, 0) -
funkcja jest ściśle malejąca
2. Ekstremum lokalne
Definicje
Funkcja f(x) ma w punkcie x0 maksimum lokalny, gdy istnieje takie sąsiedztwo S(x0, δ), że dla ∀ x ∈ S jest spełniona nierówność:
f(x) ≤ f(x0)
Definicje
Funkcja f(x) ma w punkcie x0 minimum lokalny, gdy istnieje takie sąsiedztwo S(x0, δ) że dla ∀ x ∈ S(x0, δ) jest spełniona nierówność:
f(x) ≥ f(x0)
Maksimum i minimum lokalne nazywamy ekstremami lokalnymi.
Ekstremum jest nazywane właściwym, gdy zamiast nierówności nieostrej jest spełniona jest nierówność mocna, tzn.:
f (x) < f (x0)
w przypadku maksimum właściwego, oraz
f (x) > f (x0)
w przypadku minimum właściwego.
Warunek konieczny istnienia ekstremum:
Twierdzenie (Fermata).
Jeżeli funkcja różniczkowalna f(x) ma w punkcie x0 ekstremum, to f ′(x0) =0.
Przykład 1.
f(x) = x5
f ′(x) = 5x4
f ′(x)=0 ⇒ x=0
Ale w punkcie x0 =0 funkcja f(x) nie ma ekstremum.
Przykład 2.
f(x) = | x|
Pochodna tej funkcji w punkcie x=0 nie istnieje,
ale fmin = 0.
Wniosek 1.
Jeżeli funkcja f(x) jest różniczkowalna w punkcie x0 i
f ′(x0) ≠ 0, to funkcja f(x) nie ma w punkcie x0 ekstremum lokalnego.
Wniosek 2.
Funkcja f(x) może mieć ekstremum tylko w punktach, w których pochodna nie istnieje albo jest równa zero.
Definicje
∀x ∈Df dla którego f ′(x)=0 nazywamy punktem stacjonarnym funkcji f (x), a wszystkie punkty stacjonarne oraz punkty w których pochodna nie istnieje, nazywamy punktami krytycznymi.
Warunek wystarczający istnienia ekstremum:
Twierdzenie.
Jeżeli funkcja f (x) jest ciągła w punkcie x0, jest różniczkowalna na jego sąsiedztwie i pochodna funkcji f (x) zmienia znak w sąsiedztwie tego punktu, to ma ona w tym punkcie x0 ekstremum właściwe i jest to:
maksimum lokalne, gdy zmienia się znak + na -
minimum lokalne, gdy zmienia się znak - na +
Jeśli pochodna funkcji f (x) ma stały znak w sąsiedztwie punktu x0, to funkcja f (x) w tym punkcie x0 ekstremum nie posiada.
Przykład 3.
Znajdź ekstremum i przedziały monotoniczności funkcji:
f(x) = x3 -12x2 +36x +8
Df =R
f ′(x) = 3x2 - 24x +36
Df ′ =R
f ′(x) = 0 ⇒ 3x2 -24x + 36 =0 ⇒ x2 - 8x + 12 =0
x1 = 2, x2 = 6
f ′(x) > 0 ⇒ x2 - 8x + 12 > 0 ⇒
x ∈ (-∝, 2) ∪ (6, ∝)
f ′(x) < 0 ⇒ x2 - 8x + 12 < 0 ⇒
x ∈ ( 2, 6)
x |
(-∝, 2) |
2 |
( 2, 6) |
6 |
(6, ∝) |
f ′(x) |
+ |
0 |
- |
0 |
+ |
f(x) |
↑ |
Max |
↓ |
min |
↑ |
Dla x = 2 mamy maksimum lokalny
fmax = f( 2 )= 40
A(2, 40) - punkt maksimum lokalnego
Dla x = 6 mamy minimum lokalny
fmin = f( 6 )= 8
B(6, 8) - punkt minimum lokalnego
Odp. Funkcja rośnie w przedziałach (- ∝, 2) oraz (6, ∝) i maleje w przedziale ( 2, 6).
Funkcja posiada maksimum lokalny w punkcie A(2,40).
Funkcja posiada minimum lokalny w punkcie B(6,8).
Przykład 4.
Znajdź ekstremum i przedziały monotoniczności funkcji:
f(x) = x3 + 3x2 -24x +17
Df =R
f ′(x) = 3x2 + 6x - 24
Df ′ =R
f ′(x) = 0 ⇒ 3x2 + 6x - 24 =0 ⇒ x2 + 2x - 8 =0
x1 = - 4, x2 = 2
f ′(x) > 0 ⇒ x2 + 2x - 8 > 0 ⇒
x ∈ (-∝, - 4) ∪ (2, ∝)
f ′(x) < 0 ⇒ x2 + 2x - 8 < 0 ⇒
x ∈ (- 4, 2)
x |
(-∝, - 4) |
- 4 |
(- 4, 2) |
2 |
(2, ∝) |
f ′(x) |
+ |
0 |
- |
0 |
+ |
f(x) |
↑ |
max |
↓ |
min |
↑ |
Dla x = - 4 mamy maksimum lokalny
fmax = f(-4)=97
A(-4, 97) - punkt maksimum lokalnego
Dla x = 2 mamy minimum lokalny
fmin = f(2)= - 11
B(2, -11) - punkt minimum lokalnego
Odp. Funkcja rośnie w przedziałach (- ∝, - 4) oraz (2, ∝) i maleje w przedziale (- 4, 2).
Funkcja posiada maksimum lokalny w punkcie A(- 4,97).
Funkcja posiada minimum lokalny w punkcie
B(2, -11).
Przykład 5.
Znajdź ekstremum i przedziały monotoniczności funkcji:
f(x) = ex(x2 +2x +1)
Df =R
f ′(x) = ex(x2 +2x +1) + ex(2x + 2) = ex(x2 +4x +3)
Df ′ =R
f ′(x) = 0 ⇒ x2 +4x +3 = 0 ⇒
x1 = - 1, x2 = -3
f ′(x) > 0 ⇒ x2 + 4x + 3 > 0 ⇒
x ∈ (-∝, - 3) ∪ (- 1, ∝)
f ′(x) < 0 ⇒ x2 + 4x + 3 < 0 ⇒
x ∈ (- 3, - 1)
x |
(-∝, - 3) |
- 3 |
(- 3, - 1) |
-1 |
(- 1, ∝) |
f ′(x) |
+ |
0 |
- |
0 |
+ |
f(x) |
↑ |
max |
↓ |
min |
↑ |
Dla x = - 3 mamy maksimum lokalny
fmax = f(- 3)= 4e-3
A(-3, 4e-3) - punkt maksimum lokalnego
Dla x = - 1 mamy minimum lokalny
fmin = f(-1) = 0
B(-1, 0) - punkt minimum lokalnego
Odp. Funkcja rośnie w przedziałach (- ∝, - 3) oraz (-1, ∝) i maleje w przedziale (- 3, -1).
Funkcja posiada maksimum lokalny w punkcie
A(-3, 4e-3).
Funkcja posiada minimum lokalny w punkcie
B(-1,0).
Twierdzenie.
Niech funkcja f (x) jest ciągła i ma ciągłe pochodne aż do rzędu n włącznie w przedziale (a,b). Jeśli x0 ∈(a,b)
oraz
f ′(x0) = f ′′ (x0) = … = f(n-1) (x0) =0,
ale f(n) (x0) ≠ 0. Wtedy
jeśli n jest liczbą parzystą, to w punkcie x0 funkcja osiąga ekstremum lokalne (maksimum, gdy f(n) (x0) < 0 oraz minimum, gdy f(n) (x0) > 0);
jeśli n jest liczbą nieparzystą, to w punkcie x0 funkcja nie osiąga ekstremum.
Przykład 6.
Znajdź ekstremum funkcji:
f(x) = x3 + 3x2 -24x +17
Df =R
f ′(x) = 3x2 + 6x - 24
f ′(x) = 0 ⇒ 3x2 + 6x - 24 =0 ⇒ x2 + 2x - 8 =0
x1 = - 4, x2 = 2
f ′′(x) =6x+6;
f ′′(x1) = f ′′(-4) =-18 < 0, n=2 ⇒
Dla x1 = -4 mamy maximum lokalny.
fmax = f(-4) = 97
A(-4, 97) - punkt maximum lokalnego.
f ′′(x2) = f ′′(2) =18 > 0, n=2 ⇒
Dla x2 = 2 mamy minimum lokalny.
fmin = f(2)= - 11
B(2, -11) - punkt minimum lokalnego.
Wklęsłość i wypukłość wykresu funkcji
Definicje 1
Funkcja f(x) jest wypukła (odp. wklęsła) na przedziale (a,b), jeśli odcinek łączący dwa dowolne punkty wykresu tej funkcji leży nad tym wykresem (odp. pod wykresem) z wyjątkiem końców odcinka.
Definicje 2
Funkcja f(x) jest wypukła (odp. wklęsła) w punkcie x0, jeśli istnieje takie sąsiedztwo S=S(x0, δ), że dla ∀(x ∈S)
punkty P(x, f(x)) wykresu leżą powyżej (odp. poniżej) stycznej poprowadzonej do wykresu w punkcie o odciętej x0.
funkcja jest wklęsła
funkcja jest wypukła
Definicje 3
Funkcja f(x) jest wypukła (odp. wklęsła) na przedziale
(a,b), jeśli jest wypukła (odp. wklęsła) w każdym punkcie x ∈ (a,b).
funkcja jest wklęsła
funkcja jest wypukła
Twierdzenie.
Niech funkcja f (x) jest dwukrotnie różniczkowana na przedziale (a,b). Jeśli
f ′′ (x) > 0 dla ∀x ∈(a,b), to f(x) jest wypukła na tym przedziale;
f ′′ (x) < 0 dla ∀x ∈(a,b), to f(x) jest wklęsła na tym przedziale.
Przykład 7.
Wyznaczyć przedziały wypukłości i wklęsłości funkcji:
f(x) = x4 - 6x2
Df =R
f ′(x) = 4x3 - 12x
f ′′(x) = 12x2 -12 = 12(x2 - 1) = 12 (x-1)(x+1)
f ′′(x) > 0 dla x ∈ (- ∝, -1) ∪ (1, ∝)
f ′′(x) < 0 dla x ∈ (-1, 1)
X |
(- ∝, -1) |
(-1, 1) |
(1, ∝) |
f ′′(x) |
+ |
- |
+ |
f(x) |
∪ |
∩ |
∪ |
Odp. Funkcja jest wypukła dla x ∈ (- ∝, -1) ∪ (1, ∝)
i jest wklęsła dla x ∈ (-1, 1).
Przykład 8.
Wyznaczyć przedziały wypukłości i wklęsłości funkcji:
f(x) = x lnx
Df =R+ = {x ∈R : x>0}
f ′(x) = lnx +x ⋅1/x= 1 + lnx
Df ′ =R+ = {x ∈R : x>0}
f ′′(x) = 1/x
f ′′(x) > 0 dla ∀x (x ∈ Df )
Odp. Funkcja jest wypukła dla ∀x (x ∈ Df ).
Punkty przegięcia wykresu funkcji
Definicje
Punkt P(x0, f(x0)) nazywamy punktem przegięcia krzywej o równaniu y=f(x), jeżeli funkcja f(x) jest ciąga w punkcie x0 oraz jest wklęsła w pewnym lewostronnym sąsiedztwie punktu x0 i wypukła w pewnym prawostronnym jego sąsiedztwie albo na odwrót.
Twierdzenie.
Warunkiem koniecznym na to, aby punkt P(x0, f(x0)) był punktem przegięcia krzywej o równaniu y=f(x), jest
f ′′(x0) =0
Twierdzenie (warunek wystarczający).
Jeżeli funkcja f(x) jest ciągła w punkcie x0, dwukrotnie różniczkowalna na sąsiedztwie tego punktu i druga pochodna funkcji f(x) zmienia znak przy przejściu przez x0, to punkt P(x0, f(x0)) jest punktem przegięcia krzywej o równaniu y=f(x).
Przykład 9.
Wyznaczyć punkty przegięcia funkcji
f(x) = x4e-x
f ′(x) = 4x3e-x -x4e-x = (4x3 -x4 )e-x
f ′′ (x) = (12x2-4x3)e-x - (4x3 -x4 )e-x = (x4- 8x3+ 12x2)e-x = x2(x2 - 8x + 12)e-x
f ′′ (x) = 0 dla x=0, x=2, x=6.
f ′′ (x) < 0 dla (x2 - 8x + 12) < 0 ⇒ x ∈ (2,6)
f ′′ (x) > 0 dla (x2 - 8x + 12) > 0 ⇒
x ∈ (- ∝, 2) ∪ (6, ∝), x ≠0
x |
(- ∝, 0) |
0 |
(0, 2) |
2 |
(2,6) |
6 |
(6, ∝) |
f ′′ (x) |
+ |
0 |
+ |
0 |
- |
0 |
+ |
f (x) |
∪ |
0 |
∪ |
p.p. |
∩ |
p.p. |
∪ |
f(2)= 16e-2, f(6) = 64e-6.
Odp. Punkty P1(2, 16e-2) oraz P2(6, 64e-6 ) są punktami przegięcia funkcji f(x).
Twierdzenie (warunek wystarczający).
Jeżeli funkcja f(x) spełnia następujące założenia:
Ma w pewnym sąsiedztwie punktu x0 pochodne do rzędu n (n ≥ 3) włącznie;
f(n)(x) jest ciągła w punkcie x0;
f ′′ (x0) = f ′′′ (x0) = … = f (n-1)(x0)= 0;
f(n)(x0) ≠ 0;
n jest liczbą nieparzystą,
to punkt P(x0, f(x0)) jest punktem przegięcia krzywej o równaniu y=f(x).
Przykład 10.
Wyznaczyć punkty przegięcia funkcji
f(x) = x5 - x + 3
f ′(x) = 5x4 - 1
f ′′ (x) = 20x3
f ′′′ (x) = 60x2
f(4)(x) = 120x
f(5)(x) = 120
Dla x=0
f ′(x) = f ′′ (x) = f ′′′ (x) = f(4)(x) =0
oraz
f(5)(x) = 120 ≠ 0
n=5 - liczba nieparzysta ⇒ punkt P(0,3) jest punktem przygięcia wykresu funkcji f(x).
Asymptoty wykresu funkcji
Definicje
Jeśli funkcja f(x) jest określona w przedziale ( -∝, m), gdzie m ∈R, to prosta y = cx+d jest asymptotą ukośną (lub poziomą, gdy c=0) lewostronną wykresu funkcji y=f(x) wtedy i tylko wtedy, gdy
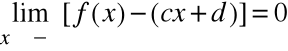
Definicje
Jeśli funkcja f(x) jest określona w przedziale ( m, ∝), gdzie m ∈R, to prosta y = ax+b jest asymptotą ukośną (lub poziomą, gdy a=0) prawostronną wykresu funkcji y=f(x) wtedy i tylko wtedy, gdy
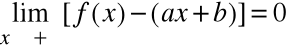
Definicje
Prosta y=ax+b jest asymptotą ukośną (albo poziomą, gdy a=0) obustronną krzywej y=f(x) wtedy i tylko wtedy, gdy jest jednocześnie ukośną (poziomą) lewostronną i prawostronną tej krzywej.
Twierdzenie (warunek konieczny i wystarczający).
Warunkiem koniecznym i dostatecznym, aby wykres funkcji f(x) miał asymptotę ukośną y = ax+b, jest istnienie dwóch granic właściwych:
1) 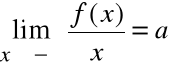
oraz 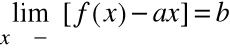
lub
2) 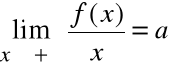
oraz 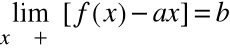
Przykład 11.
Wyznaczyć asymptoty funkcji
f(x) = 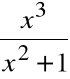
1) 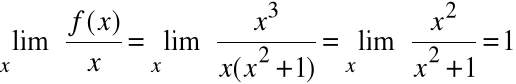
a=1
2) 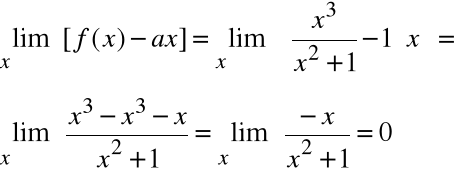
b=0
Zatem a=1, b=0. Prosta y=x jest asymptotą ukośną obustronną.
Definicje
Prostą o równaniu x=a nazywamy asymptotą pionową lewostronną wykresu funkcji f(x), gdy:
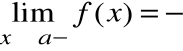
lub 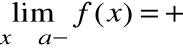
Definicje
Prostą o równaniu x=a nazywamy asymptotą pionową prawostronną wykresu funkcji f(x), gdy:
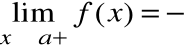
lub 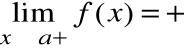
Definicje
Prostą o równaniu x=a nazywamy asymptotą pionową obustronną wykresu funkcji f(x), gdy jest jednocześnie asymptotą pionową prawostronną i lewostronną.
Przykład
f(x) = 21/x
y = 1 - asymptota pozioma obustronna
x = 0 - asymptota pionowa prawostronna
Przykład
x=π/2+πk ( k∈Z) - asymptoty pionowe obustronne
Przykład
x = x0 - asymptota pionowa obustronna
Przykład 12.
Wyznaczyć asymptoty funkcji
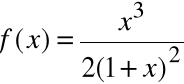
Df = R \ {-1}
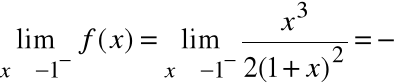
oraz 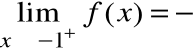
Zatem prosta x=-1 jest asymptotą pionową obustronną funkcji f(x).
Ogólny schemat badania przebiegu funkcji
I. Analiza funkcji.
Dziedzina funkcji.
Szczególne własności funkcji: parzystość, nieparzystość, okresowość itp.
Punkty przycięcia wykresu funkcji z osiami układu współrzędnych.
Ustalenie znaku funkcji.
Granice funkcji na końcach przedziałów określoności.
Punkty nieciągłości funkcji.
Asymptoty funkcji.
II. Analiza pierwszej pochodnej.
Obliczamy pierwszą pochodną.
Dziedzina pierwszej pochodnej i jej punkty nieciągłości.
Przedziały monotoniczności.
Ekstrema lokalne funkcji.
III. Analiza drugiej pochodnej.
Obliczamy drugą pochodną.
Dziedzina drugiej pochodnej i jej punkty nieciągłości.
Przedziały wklęsłości i wypukłości funkcji.
Punkty przegięcia wykresu funkcji.
IV. Ostateczny szkic wykresu funkcji.
Przykład 13.
f(x) = xex
Df=R - funkcja jest ciąłga
f(-x) = -xe-x ≠ f(x) - funkcja nie jest parzystą
f(-x) = -xe-x ≠ - f(x) = -xex - funkcja nie jest nieparzystą
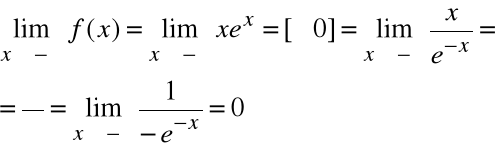
f(x)=0 ⇒ xex = 0 ⇒ x=0 ⇒ (0,0) - punkt przecięcia funkcji z osiami układu współrzędnych.
Ponieważ f(x) jest ciągła, nie posiada asymptot pionowych.
Ponieważ
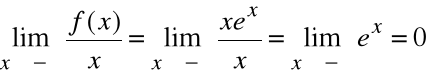
a=0
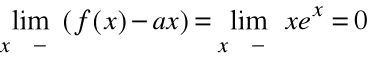
,
b=0
y=0 jest asymptotą poziomą lewostronną.
Ponieważ
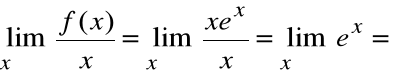
funkcja nie posiada asymptoty ukośną.
Obliczamy pierwszą pochodną:
f ′(x) = ex + xex = (1+x)ex.
Ponieważ ex > 0 dla ∀x,
a) f ′(x) = 0 ⇔ 1 +x=0 ⇔ x = -1;
b) f ′(x) > 0 ⇔ 1+x >0 ⇔ x ∈(-1, ∝)
c) f ′(x) < 0 ⇔ 1+x <0 ⇔ x ∈(- ∝, -1)
funkcja rośnie dla x ∈(-1, ∝)
funkcja maleje dla x ∈(- ∝, -1)
x=-1 - punkt minimum lokalnego
fmin = f(-1) = -e-1.
Obliczamy drugą pochodną:
f ′′ (x) = ex + (1+x)ex = (2+x)ex.
a) f ′′ (x) = 0 ⇔ 2 +x=0 ⇔ x = -2;
b) f ′′ (x) > 0 ⇔ 2+x >0 ⇔ x ∈(-2, ∝)
c) f ′′ (x) < 0 ⇔ 2+x <0 ⇔ x ∈(- ∝, -2)
funkcja f(x) jest wypukła dla x ∈(-2, ∝)
funkcja f(x) jest wklęsła dla x ∈(- ∝, -2)
x=-2 - jest punktem przegięcia
Przykład 14.
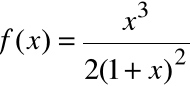
Wyszukiwarka