SPRAWOZDANIE
Ćwiczenie nr 18
Temat ćwiczenia: Wyznaczanie pK oranżu metylowego metodą spektrofotometryczną
Wyposażenie ćwiczenia :
Aparatura i urządzenia: Spektrofotometr „ Spekol ”
Zestaw probówek
2 pipety o pojemności 5 cm3
Odczynniki: Roztwór oranżu metylowego 0,0012%
Zestaw roztworów buforowych o pH: od 2,2 do 5,4
Roztwór kwasu siarkowego 0,5 m
Roztwór wodorotlenku sodowego 0,5 m
Wstęp
Wskaźniki alkacymetryczne - zwane sa także indykatorami. Charakteryzują się tym, że ich roztwory zmieniają zabarwienie przy zmianie stężenia jonów wodorowych. Istotę tego zjawiska można łatwo zrozumieć jeśli wziąć pod uwagę, że indykatory są słabymi kwasami, bądź zasadami organicznymi, a zatem ulegają w roztworach wodnych dysocjacji, przy czym przynajmniej jedna z form każdego indykatora - cząsteczki niezdysocjowane, bądź powstające w wyniku dysocjacji jony - ma wyraźne pasmo absorpcyjne w widzialnym zakresie fal elektromagnetycznych.
Rozważmy wskaźnik o charakterze kwasowym, na przykład HA, który w roztworze wodnym dysocjuje zgodnie z równaniem:
HA ↔ H+ + A-
W przypadku, gdy roztwór tego wskaźnika nie jest zbyt stężony, równowagę dysocjacji określa prawo działania masy, które zgodnie z propozycją Hendersona i Hasselbacha - można wyrazić w postaci:
pH = pK + log[A-]/[HA]
pH - wykładnik jonów wodorowych,
K - stałą dysocjacji wskaźnika HA (pK = - log K),
[A-] i [HA] - stężenia odpowiednich form tego wskaźnika [mol/dm3].
Dla naszych celów wygodnie będzie wyrazić stężenia [A-] i [HA] przez stopień dysocjacji α i całkowite stężenie wskaźnika c, które zgodnie ze stechiometrią równania dysocjacji jest równe sumie stężeń [A-] + [HA]. Z definicji stopnia dysocjacji
[A-] = α ⋅ c
stąd:
[HA] = (1 - α ) ⋅ c
więc równanie na pH możemy zapisać w postaci:
pH = pK + log [α/(α-1)]
Z podanych równań wynika, że w roztworach kwaśnych występuje praktycznie tylko forma niezdysocjowana, a w alkalicznych zdysocjowana (czyli: jeśli pH jest większe bądź równe pK - 3, to α<0,001, jeśli zaś pH jest większe lub równe pK + 3, to α > 0,999.
Jeżeli obie formy wskaźnika są barwne - ( np. w oranżu metylowego) - to barwa roztworu kwaśnego jest barwą dopełniającą do tej, którą absorbują cząsteczki niezdysocjowane HA, analogicznie absorpcja światła przez jony A- określa barwę roztworu alkalicznego.
Ilościowo absorpcję światła przez roztwór możemy opisać równaniem:
E = εA- ⋅l⋅[A-] + εHA⋅l⋅[HA]
lub
E = (εA-- εHA) ⋅ l⋅ c⋅ α+ εHA⋅ l⋅ c
gdzie:
-E - absorbancja ( ekstynkcja ) roztworu,
-l - grubością warstwy roztworu przez którą przechodzi światło ,
-εA- i εHA - molarne współczynniki absorpcji odpowiednich form wskaźnika (εA- i εHA są to charakterystyczne funkcyje, ponieważ zależą od długości fali ).
Zmiana barwy roztworu wywołana zmianą pH jest tym wyraźniejsza, im bardziej pH roztworu jest zbliżone do pK wskaźnika. Aby tego dowieść wystarczy zauważyć, że
dla c= const.
![]()
gdzie:
- 2,303 jest to przybliżona wartość przelicznika logarytmów dziesiętnych na naturalne (dokładna wartość wynosi ln 10).
![]()
osiąga maksimum dla![]()
a wtedy pH= pK
Na tym spostrzeżeniu opiera się między innymi przybliżona metoda wizualnego określania pH roztworów, a także jedna z najstarszych metod wyznaczania pK wskaźników. Metoda ta polega na tym, że jeżeli zmierzymy ekstynkcję roztworów danego wskaźnika w wodnych roztworach buforowych o różnych wartościach pH(zachowując stałe stężenie wskaźnika
c= const. ) i stałą długość fali (λ= const.) w całej serii pomiarów, a wykreślimy krzywa
E= f (pH), to punkt przecięcia tej krzywej odpowiada wartości pH= pK. Ze względu na to, że metoda graficznego różniczkowania jest mało dokładna, punkt przegięcia wyznacza się praktycznie w ten sposób, iż mierzy się dodatkowo ekstynkcje dwóch roztworów wskaźnika: roztworu kwaśnego, Ek o pH< pK- 3 oraz zasadowego Ez o pH> pK+3, przy zachowaniu tego samego stężenia wskaźnika i tej samej długości fali, jakie stosowano w serii badań, na podstawie których sporządzono wykres E = f (pH), a następnie oblicza się średnią arytmetyczną z obydwu wyników pomiarów:
E= (Ek+ Ez)
i odczytuje z krzywej E= f (pH) wartość pH odpowiadającą tej wartości ekstynkcji; można łatwo dowieść, że tak wyznaczona wartość pH jest równa pK wskaźnika.
Warto jeszcze podkreślić , że pK można wyznaczyć tym dokładniej, im większa będzie bezwzględna wartość różnicy współczynnika absorpcji εA- i εHA. Dlatego jest wskazane, aby pomiary ekstynkcji były przeprowadzane przy takiej samej długości fali, dla której wyrażenie
(εA-- εHA ) osiąga maksimum ( dla oranżu metylowego najodpowiedniejsza jest długość fali 525nm).
Celem ćwiczenia było wyznaczenie molowych współczynników absorbcji εA i εHA dla badanych roztworów oranżu metylowego, określenie wartości pH roztworu w punkcie przegięcia i porównanie jej z wartością pK wskaźnika podaną w „Poradniku fizyko - chemicznym”.
OPRACOWANIE WYNIKÓW
Lp |
pH roztworu |
Ekstynkcja |
Stopień dysocjacji α |
Pochodna |
1 |
kwaśny |
1 |
- |
- |
2 |
2.2 |
0,96 |
0,111816 |
-0,20013 |
3 |
2.6 |
0,7 |
0,240253 |
-0,36782 |
4 |
3.0 |
0,45 |
0,442688 |
-0,49716 |
5 |
3.2 |
0,3 |
0,557312 |
-0,49716 |
6 |
3.4 |
0,19 |
0,666139 |
-0,44816 |
7 |
3.6 |
0,155 |
0,759747 |
-0,36782 |
8 |
3.8 |
0,15 |
0,833662 |
-0,27944 |
9 |
4.0 |
0,145 |
0,888184 |
-0,20013 |
10 |
4.4 |
0,135 |
0,952273 |
-0,09159 |
11 |
4.8 |
0,13 |
0,980438 |
-0,03865 |
12 |
5.4 |
0,13 |
0,995013 |
-0,01 |
13 |
zasadowy |
0.125 |
- |
- |
Stężenie procentowe oranżu metylowego należy przeliczyć na stężenie molowe przy założeniu , że d = 1g/dm3.
100 cm3 roztworu - zawiera 0,0012g oranżu metylowego
5 cm3 roztworu - zawiera x g oranżu metylowego
z podanej zależności wynika
x = 0,00006 g
1 mol - zawiera 341,45g oranżu metylowego
y moli - zawiera 0,00006 g oranżu metylowego
z danej zależności wynika:
y = 1,757⋅10-7mola
Następnie wyliczam stężenie molowe oranżu metylowego uwzględniając zmiany objętości wywołanej dodaniem kwasu lub zasady według podanego poniżej wzoru:
![]()
gdzie:
V = 2⋅5cm3 = 10 cm3 = 10⋅10-3 dm3
![]()
Obliczam wartość współczynników εA- i εHA korzystając ze wzorów:
E=εHA⋅c⋅l z którego wyliczam ![]()
, E=εA⋅c⋅l z którego wyliczam ![]()
l=1,001cm=0,1001dm
![]()
![]()
[dm2/mol]
![]()
![]()
[dm2/mol]
Gdy znamy wartości molowych współczynników adsorpcji możemy obliczyć wartość ekstynkcji roztworu dla ![]()
ze wzoru :
E=(εA-εHA)⋅l⋅CM⋅α+εHA⋅l⋅CM
E = 0.57
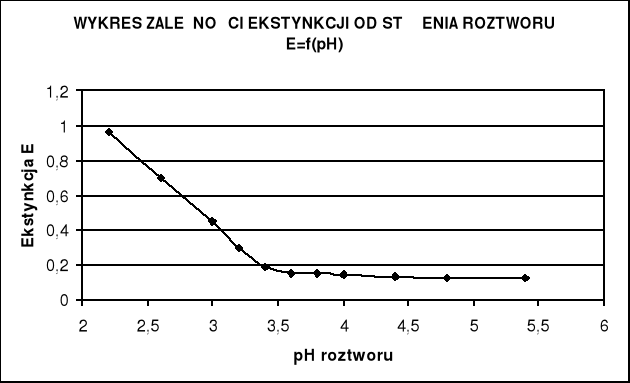
Odczytując z wykresu zamieszczonego poniżej, punktowi przegięcia odpowiada ekstynkcja równa około:
E=0,4
pK oranżu metylowego zgodnie z danymi podanymi w „Poradnik fizykochemiczny” wynosi pK=3,46.
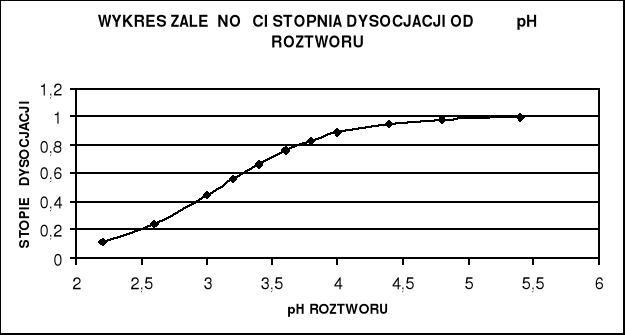
Obliczam stopień dysocjacji α oranżu metylowego w poszczególnych próbkach wiedząc , że pK wynosi 3,1. Wyniki zamieszczam w tabeli , a korzystam ze wzoru
![]()
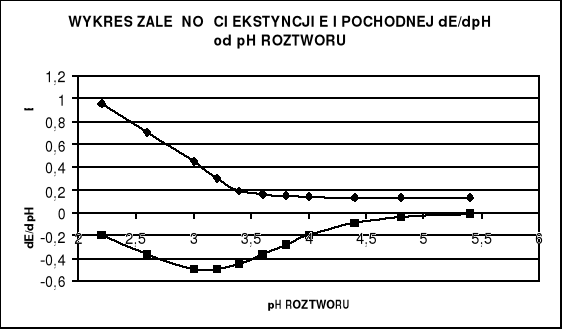
Obliczam wartości pochodnej ![]()
dla poszczególnych roztworów z następującego wzoru:
![]()
2,303⋅(εA-εHA)⋅l⋅c⋅α⋅(1-α)
wyniki zamieszczam w tabeli.
Wykreślam zależność E = f(pH) , (dE/dpH) = f(pH) oraz α = f(pH).
Z równania :
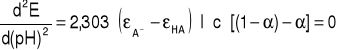
wynika , że druga pochodna funkcji E = f (pH) jest równa zero dla ![]()
w tym punkcie pierwsza pochodna osiąga ekstremum , a funkcja E = f (pH) ma punkt przegięcia. Wówczas zgodnie z równaniem :
![]()
pH roztworu jest równe co do wartości pK oranżu metylowego
pH = pK
Na tej podstawie z ostatniego wykresu odczytujemy , że punktowi przegięcia funkcji E = f (pH) odpowiada wartość pH równa 3,1, czyli pK oranżu metylowego wynosi :
pK = 3,1
pK oranżu metylowego zgodnie z danymi podanymi w „Poradnik fizykochemiczny” wynosi 3,46 natomiast pH oranżu odczytane z wykresu jest zbliżone do pK podanego w literaturze.
Wyszukiwarka