Politechnika Wrocławska
Filia Wałbrzych
Temat: obliczanie stateczności skarpy.
Kamińska Anna
Nr albumu 130414
Cel ćwiczenia projektowego.
Dla zadanych warunków gruntowych wyrobiska ustalić schematy utraty stateczności, dobrać metody obliczeniowe oraz sprawdzić stateczność skarpy o nachyleniu 1:2 przy zadanym obciążeniu q= 100kPa
Ćwiczenie projektowe ma na celu poznanie umiejętności określenia , czy badana skarpa jest stateczna, czy wręcz przeciwnie oraz określenie czy konieczne jest wykonanie prac mających na celu przeciwdziałanie ewentualnemu osunięciu się skarpy.
Zakres mojego opracowania wchodzi sprawdzenie stateczności skarpy o nachyleniu 1:2. skarpa jest obciążona qw=100kPa na długości 10m. Obciążenie to jest oddalone od krawędzi skarpy o 0m.
Opis warunków gruntowych
Badana skarpa zbudowana jest z dwóch warstw geotechnicznych. Jako pierwsza licząc od poziomu zalega warstwa piasku średniego (Ps), a jako druga warstwa iłu pylastego(IP).
Pod warstwą druga zalega podl9oże skalne.
Warstwa I : piasek średni (Ps)- miąższość warstwy wynosi 4m.
Zawartość ziaren o średnicy większej niż 0,5 mm wynosi nie więcej niż 50%, lecz zawartość ziaren o średnicy większej niż 0,25 mm wynosi więcej niż 50%.
0,5mm>d50>0,25mm
stopień zagęszczenia 0,33<ID<0,67 i jest to grunt średnio zagęszczony. Stopień wilgotności 0,4<Sr<0,8 i jest on wilgotny. Jego wilgotność właściwa wynosi 14%. Jego gęstość ρ = 2,65
ID=0,50, więc mamy tu ρ=1,85
Warstwa II : ił piaszczysty (Ip)- miąższość wynosi 6m
Ił piaszczysty to mieszanina 3 frakcji : pyłowej (0-20%), piaszczystej (50-70%) i iłowej
(30-50%). Ił piaszczysty jest gruntem makroskopowo jednorodnym.
0<IL< 0,25 jest to grunt twardoplastyczny. Stopień wilgotności 0<Sr<o,4 jest to grunt mało wilgotny. Jego wilgotność właściwa to 18%. Jego gęstość g=2,70
IL=0,20 mamy tu więc ρ=1,90
nazwa
|
Grubość warstwy |
IL |
ID |
Sr |
Wilgotność |
Grupa kansolida- cyjna |
Ciężar objętościowy |
Obliczeniowe cechy wytrzymałościowe
|
|
|
|
|
|
|
|
|
|
Φ |
C |
Ps |
4m |
- |
0,50 |
14% |
MW |
- |
18,5 |
33˚ |
- |
Ip |
6m |
0,20 |
- |
18% |
MW |
D |
19,0 |
11˚ |
50 |
Tabela1
Nr paska |
h[cm] |
b[cm] |
bi[m] |
P |
Gi |
q |
Wi |
α |
sin α |
cos α |
Bi |
Ni |
Li |
Ti |
1 |
2,0 |
1,0 |
2,0 |
1,0 |
18,5 |
0,0 |
18,5 |
50,0 |
0,77 |
0,64 |
14,2 |
11,9 |
3,1 |
7,73 |
2 |
2,2 |
1,0 |
2,0 |
2,2 |
41,3 |
100,0 |
141,3 |
55,8 |
0,83 |
0,56 |
116,7 |
79,5 |
3,6 |
51,67 |
3 |
2,4 |
1,0 |
2,0 |
2,4 |
45,0 |
100,0 |
145,0 |
84,9 |
1,0 |
0,09 |
144,4 |
13,1 |
22,1 |
8,51 |
4 |
2,6 |
1,3 |
2,6 |
3,38 |
63,4 |
100,0 |
163,4 |
80,5 |
0,99 |
0,17 |
161,1 |
27,1 |
15,7 |
17,61 |
5 |
2,8 |
0,9 |
2,8 |
2,52 |
47,3 |
100,0 |
147,3 |
80,1 |
0,99 |
0,17 |
145,1 |
25,3 |
10,5 |
529,91 |
6 |
3,0 |
1,1 |
2,2 |
3,3 |
61,9 |
100,0 |
161,9 |
75,8 |
0,97 |
0,25 |
156,9 |
39,9 |
8,9 |
452,74 |
7 |
2,9 |
1,2 |
2,4 |
3,48 |
65,3 |
0 |
65,3 |
76,6 |
0,97 |
0,23 |
63,5 |
15,1 |
10,3 |
517,93 |
8 |
2,5 |
1,3 |
2,6 |
2,6 |
48,8 |
0 |
48,8 |
69,2 |
0,393 |
0,36 |
45,6 |
17,4 |
7,3 |
368,37 |
9 |
2,0 |
1,4 |
2,8 |
2,8 |
52,5 |
0 |
52,5 |
60,5 |
0,87 |
0,49 |
45,7 |
25,9 |
5,7 |
290,02 |
10 |
1,6 |
1,5 |
3,0 |
2,4 |
45,0 |
0 |
45,0 |
53,0 |
0,80 |
0,60 |
35,9 |
27,1 |
5,0 |
255,26 |
11 |
1,2 |
1,7 |
3,4 |
2,04 |
38,3 |
0 |
38,3 |
41,4 |
0,66 |
0,75 |
25,3 |
28,7 |
4,5 |
230,57 |
12 |
0,5 |
3,0 |
6,0 |
1,5 |
28,1 |
0 |
28,1 |
18,6 |
0,32 |
0,95 |
8,9 |
26,7 |
6,3 |
320,18 |
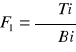
=3,16 ΣBi=963,3 ΣTi=3050,5
Tabela2
Nr paska |
h[cm] |
b[cm] |
bi |
P |
Gi |
q |
Wi |
α |
sin α |
cos α |
Bi |
Ni |
Li |
Ti |
1 |
2,0 |
0,7 |
1,4 |
1,4 |
26,3 |
100 |
126,3 |
81,43 |
0,99 |
0,15 |
124,8 |
18,9 |
9,4 |
12,28 |
2 |
2,2 |
1,0 |
2,0 |
2,2 |
41,3 |
100 |
141,3 |
72,8 |
0,96 |
0,3 |
134,9 |
41,8 |
6,8 |
27,17 |
3 |
2,6 |
1,2 |
2,4 |
3,12 |
58,5 |
100 |
158,5 |
72,4 |
0,95 |
0,3 |
151,0 |
48,0 |
7,9 |
31,20 |
4 |
2,9 |
1,4 |
2,8 |
4,06 |
76,1 |
100 |
176,1 |
78,9 |
0,98 |
0,19 |
172,8 |
34,1 |
14,4 |
22,16 |
5 |
3,2 |
1,4 |
2,8 |
4,48 |
84,0 |
100 |
184,0 |
73,7 |
0,96 |
0,28 |
176,6 |
51,8 |
9,9 |
505,05 |
6 |
3,0 |
1,2 |
2,4 |
3,6 |
67,5 |
0 |
67,5 |
75,8 |
0,97 |
0,25 |
65,4 |
16,6 |
9,7 |
488,22 |
7 |
2,6 |
1,2 |
2,4 |
3,12 |
58,5 |
0 |
58,5 |
74,5 |
0,96 |
0,27 |
56,4 |
15,7 |
8,9 |
448,14 |
8 |
2,2 |
1,0 |
2,0 |
2,2 |
41,3 |
0 |
41,3 |
70,5 |
0,94 |
0,33 |
38,9 |
13,8 |
6,0 |
302,67 |
9 |
2,0 |
1,3 |
2,6 |
2,6 |
48,8 |
0 |
48,8 |
63,4 |
0,89 |
0,45 |
43,6 |
21,9 |
5,8 |
294,25 |
10 |
1,5 |
1,2 |
2,4 |
1,8 |
33,8 |
0 |
33,8 |
57,0 |
0,84 |
0,54 |
28,3 |
18,4 |
4,4 |
225,57 |
11 |
1,0 |
1,9 |
3,8 |
1,9 |
35,6 |
0 |
35,6 |
31,0 |
0,52 |
0,86 |
18,4 |
30,5 |
4,4 |
227,92 |
12 |
0,6 |
2,0 |
4,0 |
1,2 |
22,5 |
0 |
22,5 |
34,4 |
0,56 |
0,83 |
12,7 |
18,6 |
4,8 |
243,67 |
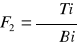
=2,76 ΣBi=1023,8 ΣTi=2828,24
Tabela3
Nr paska |
h[cm |
b[cm] |
bi |
P |
Gi |
q |
Wi |
α |
sin α |
cos α |
Bi |
Ni |
Li |
Ti |
1 |
0,9 |
2,5 |
5,0 |
2,25 |
42,2 |
100 |
142,2 |
21,99 |
0,37 |
0,93 |
53,2 |
131,8 |
5,4 |
85,62 |
2 |
1,9 |
0,9 |
1,8 |
1,71 |
32,1 |
100 |
132,1 |
28,0 |
0,47 |
0,88 |
61,9 |
116,6 |
2,0 |
75,79 |
3 |
2,2 |
1,1 |
2,2 |
2,41 |
45,2 |
100 |
145,2 |
70,5 |
0,94 |
0,33 |
136,8 |
48,6 |
6,6 |
31,59 |
4 |
2,8 |
1,0 |
2,0 |
2,74 |
51,4 |
100 |
151,4 |
78,2 |
0,98 |
0,21 |
148,1 |
31,2 |
9,7 |
20,28 |
5 |
3,0 |
1,0 |
2,0 |
2,80 |
52,5 |
100 |
152,5 |
79,5 |
0,98 |
0,18 |
149,9 |
27,8 |
11,0 |
555,39 |
6 |
2,9 |
1,0 |
2,0 |
3,0 |
56,3 |
0 |
56,3 |
78,9 |
0,98 |
0,19 |
55,2 |
10,9 |
10,3 |
517,11 |
7 |
2,5 |
1,2 |
2,4 |
3,19 |
59,8 |
0 |
59,8 |
71,7 |
0,95 |
0,31 |
56,3 |
18,8 |
7,6 |
383,64 |
8 |
2,1 |
1,3 |
2,6 |
3,0 |
56,3 |
0 |
56,3 |
64,4 |
0,90 |
0,43 |
50,7 |
24,3 |
6,0 |
304,71 |
9 |
1,7 |
1,2 |
2,4 |
2,52 |
47,3 |
0 |
47,3 |
71,0 |
0,95 |
0,33 |
44,7 |
15,4 |
7,4 |
372,98 |
10 |
1,5 |
1,1 |
2,2 |
2,04 |
38,3 |
0 |
38,3 |
65,3 |
0,91 |
0,42 |
34,7 |
16,0 |
5,3 |
268,10 |
11 |
1,3 |
1,5 |
3,0 |
1,95 |
36,6 |
0 |
36,6 |
69,8 |
0,94 |
0,35 |
34,7 |
12,6 |
8,7 |
437,44 |
12 |
0,5 |
3,2 |
6,4 |
1,6 |
30,0 |
0 |
30,0 |
64,4 |
0,90 |
0,43 |
27,1 |
13,0 |
14,8 |
742,52 |
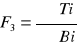
=4,45 ΣBi=853,3 ΣTi=3795,22
![]()
3,16>2,76<4,45
x1=0 F1=3,16
x2=0,6 F2=2,76
x3=5,7 F3=4,45
![]()
F1=ax12+bx1+c x1=0, F1 =3,16
c=3,16
F2=ax22+bx2+3,16=2,76
F3=ax32+bx3+3,16=4,45
c=3,16
a(0,6)2+0,6b+3,16=2,76
a(5,7)2+5,7b+3,16=4,45
a=0,175
b=-0,772
c=3,16
F(x)=0,175x2-0,772x+3,16
F΄(x)=0,350x-0,772
F΄(x)=0
0,350x0-0,772=0
x0=2,21
Fmin= F(x0)
F(x0)= 0,175·(2,21)2-0,772·2,21+3,16=2,31
F(x0)=2,31kN
Wnioski:
Dla zadanych warunków gruntowych przeprowadziłam obliczenia sprawdzające skarpę, w wyniku tych obliczeń otrzymałam Fmin=2,31kN dla x0=2,21[m]. Przy obliczaniu stateczności zboczy z gruntów niespoistych przyjmuje się płaszczyznę poślizgu przebiegającą równolegle do skarpy (zsów). Przyjmuje, że mija skarpa jest stateczna.
WZORY
bi= b*2
P=h*b
Gi=P*γ
Wi=Gi+q
α=h/b
Bi=Wi*sinα
Ni=Wi*cosα
Li=bi/cosα
Ti=Ni*tgΦ+c*Li

F- wskaźnik stateczności
Bi- siła styczna
Ni- siła prostopadła do zbocza
Wyszukiwarka