Wykład 2

Granica ciągu

Definicja 1. Ciągiem nieskończonym nazywamy dowolną funkcję określoną na zbiorze liczb naturalnych.

czytaj.: n-ty wyraz ciągu

Określenie: Prawie wszystkie wyrazy ciągu oznacza: wszystkie z wyjątkiem ich skończonej ilości.

Definicja 2. Liczbę rzeczywistą a nazywamy granicą ciągu
, jeżeli dla każdego dodatniego, dowolnie małego ε istnieje taka liczba
, ze wszystkie wyrazy o numerach większych od
spełniają nierówność
.

Zatem można obrazowo stwierdzić, iż liczba a jest granicą ciągu
, gdy prawie wszystkie wyrazy (czyli wszystkie oprócz skończonej ilości) tego ciągu leżą dowolnie blisko a (czyli w odległości mniejszej niż dowolnie małe ε).

Fakt ten zapisujemy symbolicznie:
lub

Wniosek: Granica ciągu stałego jest równa wartości jego wyrazów.

Twierdzenie 1

Niech

Wówczas 1)

2)

3)

Definicja 3. Mówimy, że ciąg
ma granicę równą
, jeżeli dla dowolnie dużej, dodatniej liczby M, istnieje taka liczba
, ze wszystkie wyrazy o numerach większych od
spełniają nierówność
.

Zatem można obrazowo stwierdzić, iż granicą ciągu
jest,
, gdy prawie wszystkie wyrazy tego ciągu są większe od dowolnie dużej liczby rzeczywistej M.

Wniosek

Definicja 4. Mówimy, że ciąg
ma równą granicę
,

Spróbujemy rozszerzyć twierdzenie 1 na niektóre przypadki granic: „
”oraz „
”

1) Jeżeli
to

2) Jeżeli
to

3) Jeżeli
to

4)Jeżeli

5) Jeżeli

6) Jeżeli

7)

8)

9)

10)

11)

Uwaga. Przytoczone twierdzenia można „skrótowo” zamieścić w tabelach, które ułatwią szybkie dotarcie do właściwej informacji:

Poniższa tabela zawiera informacje o granicy iloczynu ciągów w przypadku różnych wariantów granic jego czynników.

an→	a>0	a<0	0	-∞	+∞
bn→
b>0	ab	ab	0	-∞	+∞
b<0	ab	ab	0	+∞	-∞
0	0	0	0	?	?
-∞	-∞	+∞	?	+∞	-∞
+∞	+∞	-∞	?	-∞	+∞

Opracuj podobne tabele dla sumy i ilorazu ciągów

Symbole nieoznaczone

Twierdzenie 2

Twierdzenie 3 (o trzech ciągach)

Dane są ciągi:
takie, że
oraz

Wówczas

Przykład:

Definicja 5. Ciąg
nazywamy ciągiem rosnącym, jeżeli

Ciąg
nazywamy ciągiem słabo rosnącym, jeżeli

Określenie. Ciągi: rosnące, słabo rosnące, malejące, słabo malejące określamy jako ciągi monotoniczne.

Definicja 6. Ciąg
nazywamy ciągiem ograniczonym od góry, jeżeli spełnia warunek

Definicja 7

Określenie

Twierdzenie 4 (o granicy ciągu monotonicznego)

Jeżeli ciąg monotoniczny
jest ograniczony z góry, to posiada granicę skończoną.

Jeśli zaś jest nieograniczony, to zmierza do
.

Liczba Eulera

Rozważmy ciąg:

Można udowodnić, że jest to ciąg monotoniczny i ograniczony, zatem na mocy tw.4 posiada granicę. Jest nią jednak liczba niewymierna (stąd oznaczenie za pomocą litery e) co również można/należałoby udowodnić.(Dowody można znaleźć np. w podręczniku Fichtenholza)

e=2,718281828459045....

Twierdzenie 5.

Jeżeli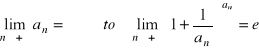

Opracowanie dr Elżbieta Badach

Na podstawie:

Fichtencholz G.M. Rachunek różniczkowy i całkowy PWN Warszawa 1985

1

a+ε

a

a-ε

n₀