STATYKA PŁYNÓW
Tensor naprężeń i jednostkowa siła powierzchniowa dla płynu w spoczynku
Prędkość płynu ![]()
, zatem w płynie nie występują naprężenia styczne:
![]()
.
Wartości naprężeń normalnych nie mogą zależeć od orientacji układu współrzędnych, zatem muszą być sobie równe:
![]()
.
Tensor naprężeń w płynie przybiera w związku z tym postać:
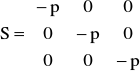
.
Jednostkowa siła powierzchniowa jest w związku z tym wyrażona następująco:
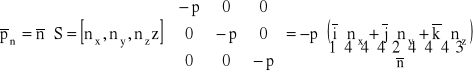
,
![]()
.
Z powyższej zależności wynika, że jednostkowa siła powierzchniowa w danym punkcie powierzchni płynu jest w przypadku płynu w spoczynku wektorem o module równym p, prostopadłym do powierzchni (![]()
⊥ A) i skierowanym przeciwnie do wektora kierunkowego powierzchni w tym punkcie.
Równanie równowagi płynu w spoczynku
Równowaga obszaru płynu V ograniczonego powierzchnią zamkniętą A pozostającego
w spoczynku wymaga, aby suma sił zewnętrznych (masowych i powierzchniowych) działających na obszar była równa zeru:
![]()
.
Z twierdzenia G-G-O wynika, że:
![]()
,
zatem: ![]()
.
Ponieważ obszar V jest dowolny, zatem funkcja podcałkowa musi być równa zeru:
![]()
,
stąd: ![]()
− warunek równowagi płynu w spoczynku.
Prawo Pascala
Jeżeli na płyn nie działają żadne siły masowe: ![]()
,
to ciśnienie w całym obszarze płynu jest stałe: p = const.
(Jeżeli ![]()
, to z równania równowagi płynu w spoczynku wynika, że ![]()
, zatem:
![]()
).
Płyn w potencjalnym polu sił masowych
Potencjał pola jednostkowych sił masowych
Jeżeli![]()
, to istnieje potencjał U pola jednostkowych sił masowych taki, że:
![]()
.
Powyższe stwierdzenie łatwo udowodnić biorąc pod uwagę równość drugich pochodnych mieszanych funkcji ciągłej (dowód był przedstawiony na wykładzie).
Równanie różniczkowe potencjału pola jednostkowych sił masowych otrzymamy mnożąc skalarnie obie strony wyrażenia ![]()
przez wektor dowolnego przesunięcia elementarnego ![]()
:
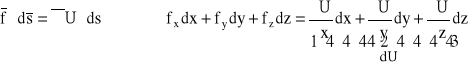
,
stąd: ![]()
.
Wyrażenie opisujące potencjał pola jednostkowych sił masowych w punkcie o współrzędnych (x,y,z) otrzymamy całkując równanie różniczkowe potencjału (funkcja wielu zmiennych!):
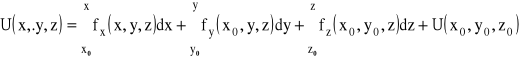
,
gdzie: x0,y0,z0 − współrzędne dowolnie wybranego punktu stałego w całkowaniu.
Powierzchnie ekwipotencjalne (U=const)
Powierzchnią ekwipotencjalną nazywamy powierzchnię, na której w każdym jej punkcie wartość potencjału jednostkowych sił masowych jest taka sama. Zatem na powierzchni ekwipotencjalnej U=const. W polu potencjału U istnieje nieskończenie wiele takich powierzchni, przy czym na każdej z nich wartość potencjału jest inna, natomiast różniczka zupełna potencjału dU=0. Przyrównując prawą stronę przedstawionego powyżej równania różniczkowego potencjału jednostkowych sił masowych do zera (dU=0) otrzymamy równanie różniczkowe rodziny powierzchni ekwipotencjalnych:
![]()
.
Równanie w postaci całkowej otrzymamy całkując powyższe równanie różniczkowe:
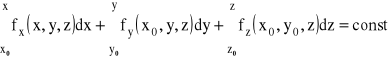
.
Własności powierzchni ekwipotencjalnych:
Powierzchnia ekwipotencjalna jest prostopadła w każdym swoim punkcie do wektora jednostkowej siły masowej w tym punkcie. Mnożąc skalarnie wyrażenie
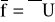
przez dowolne przesunięcie elementarne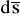
na powierzchni U=const (styczne do tej powierzchni), otrzymamy:
![]()
.
Oznacza to, że ![]()
. Ponieważ ![]()
zatem ![]()
. (Ogólniej oznacza to, że ![]()
, zatem wektor gradientu pola skalarnego (w tym przypadku pola U) jest prostopadły do powierzchni stałej wartości skalara).
Na powierzchni ekwipotencjalnej ciśnienie jest stałe: p=const (powierzchnia izobaryczna).
Z warunku równowagi płynu w spoczynku, mamy:
![]()
(iloczyn skalarny)
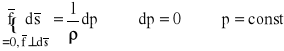
.
Na powierzchni ekwipotencjalnej gęstość płynu jest stała: ρ=const (powierzchnia izosteryczna).
Warunek równowagi płynu w spoczynku przedstawmy w postaci: ![]()
i obliczmy rotację obu stron równania:
![]()
(rotacja gradientu skalara jest równa zero, co łatwo sprawdzić biorąc pod uwagę równość drugich pochodnych mieszanych funkcji ciągłej).
Zatem: ![]()
.
Ponieważ ![]()
, zatem ![]()
− patrz uwaga powyżej.
Wynika stąd, że: ![]()
, co oznacza, że![]()
. Ponieważ ![]()
, a wektor![]()
, zatem jest to ta sama powierzchnia.
Powierzchnia swobodna cieczy jest powierzchnią ekwipotencjalną, ponieważ jest to powierzchnia, na której panuje stałe ciśnienie znajdującego się nad nią gazu (patrz pkt 2).
Powierzchnia rozdziału dwóch cieczy nie mieszających się ze sobą jest powierz-chnią ekwipotencjalną. Zakładając dla cieczy ρ=const, na powierzchni rozdziału gęstość każdej z cieczy jest stała. Jest to zatem powierzchnia izosteryczna, która jest powierzchnią ekwipotencjalną (patrz pkt 3).
Równanie rozkładu ciśnienia w płynie w potencjalnym polu sił masowych
Ponieważ: ![]()
, zatem z równania równowagi płynu w spoczynku mamy:
![]()
.
Stąd: ![]()
(dowolne przesunięcie elementarne, iloczyn skalarny)
![]()
,
zatem: ![]()
.
Rozkład ciśnienia w cieczy w ziemskim polu grawitacyjnym
(wzór manometryczny)
Założenia: ![]()
(płyn nieściśliwy); ![]()
, gdzie: ![]()
- przyspieszenie ziemskie (wektor).
Ponieważ: ![]()
zatem
pole sił masowych jest potencjalne (posiada potencjał U) .
Rozkład ciśnienia opisuje więc równanie różniczkowe:
![]()
,
stąd: ![]()
.
Dla: z = 0, p = p0,
gdzie: p0 - ciśnienie w początku układu współrzędnych,
otrzymamy: C = p0.
Zależność opisująca rozkład ciśnienia w cieczy w ziemskim polu grawitacyjnym, zwana wzorem manometrycznym, przybiera zatem postać:
![]()
.
Uwaga: Znak minus w powyższym wzorze wynika ze zwrotu wektora przyspieszenia ziemskiego, który jest przeciwny do skierowania osi z przyjętego układu współrzędnych. Jeżeli początek układu współrzędnych umieścimy na lustrze cieczy, ponad którą panuje ciśnienie atmosferyczne (p0=pa), a głębokość zanurzenia wybranego punktu oznaczymy jako h, wówczas współrzędna położenia tego punktu z = - h. Ciśnienie na głębokości h będzie wtedy opisane zależnością:
![]()
.
Literatura:
1. W. Prosnak: Mechanika Płynów, tom I
Część II, Statyka Płynów, Rozdział 1: Wiadomości ogólne - całość.
2. J. Bukowski, P. Kijkowski: Kurs Mechaniki Płynów
Rozdz. 2.4 Równowaga płynu - podpunkty 2.4.1; 2.4.2
Dr inż. Janusz Bidziński Mechanika płynów - materiały pomocnicze dla studiów niestacjonarnych
y
z
x
![]()
0
p
0
x
z
![]()
dA
![]()
V
A
dV
y
![]()
Wyszukiwarka