Wykład X. Półprzewodniki domieszkowane.

Wykres VIII-8 z poprzedniego rozdziału pokazuje jak silnie może zmieniać się koncentracja nośników a co za tym idzie przewodnictwo półprzewodników od warunków zewnętrznych ( temperatury). Równie silny efekt uzyskamy jeśli będziemy potrafili kontrolować koncentrację nośników w pasmach w inny sposób . Przykładem takiego działania jest intencjonalne domieszkowanie kryształów półprzewodnikowych atomami innych pierwiastków. Np. przewodnictwo krzemu wzrasta 1000 razy po domieszkowaniu go borem w stosunku 1 atom boru na 10000 atomów krzemu. Podobnie jest gdy domieszkujemy krzem fosforem.

Atomy domieszki dostarczają do materiału dodatkowych nośników prądu. Jeśli nośnikami są elektrony domieszki te nazywamy donorami, jeśli nośnikami są dziury domieszki nazywamy akceptorami. W obu przypadkach przewodnictwo, jakie wówczas występuje nazywamy przewodnictwem domieszkowym.

Stany domieszkowe.

Wszystkie półprzewodniki krystaliczne, które tu omawiamy posiadają wiązania kowalencyjne, w których 8 elektronów przypada na parę ( dwa) atomów tworzących bazę struktury krystalicznej. Rozważmy przykładowo: Si-Si, Ge-Ge (w obu przypadkach mamy 4 elektrony walencyjne od każdego atomu), Ga-As ( 3 elektrony Ga i 5 elektronów As) , Zn-Se (2 elektrony od Zn i 6 elektronów od Se) itp. W stanie podstawowym wszystkie 8 elektronów obsadza poziomy w pasmie walencyjnym, zapełniając je całkowicie. Pasmo przewodnictwa pozostaje puste.

Wyobraźmy sobie teraz , że atom pierwiastka macierzystego został zastąpiony atomem posiadającym o jeden elektron walencyjny więcej, np. azot lub fosfor zastępujący atom krzemu, lub selen zastępujący atom arsenu w GaAs. We wszystkich tych przypadkach nie ma już wolnych stanów w pasmie walencyjnym wobec czego dodatkowy elektron powinien znaleźć się w pasmie przewodnictwa. Przewodnictwo, z którym wówczas mamy do czynienia nazywa się przewodnictwem elektronowym ( lub typu n) a sam półprzewodnik półprzewodnikiem typu n . Domieszki tego dostarczające elektrony nazywamy donorami

Co stanie się gdy atom macierzysty zostaje zastąpiony przez atom pierwiastka , posiadającego mniej elektronów walencyjnych, np. bor i glin w krzemie, kadm zastępujący gal w GaAs. Brak elektronu w wiązaniu krystalicznym atomu domieszki z pozostałymi atomami sieci powoduje pojawienie się dziury w pasmie walencyjnym. Przewodnictwo , z którym mamy tu do czynienia nazywamy przewodnictwem dziurowym lub przewodnictwem typu p a sam półprzewodnik półprzewodnikiem typu p. Domieszki dostarczające dziur nazywamy akceptorami.

Rozważmy dokładniej kinetykę dodatkowych nośników prądu. Elektron, dla którego nie ma wolnego stanu w pasmie walencyjnym powinien znaleźć się w pasmie przewodnictwa. W przestrzeni rzeczywistej może znajdować się więc w dowolnym miejscu w sieci. Zauważmy jednak, że po utracie jednego elektronu atom donora będzie miał nie skompensowany dodatni ładunek równy +e. W konsekwencji pojawi się siła przyciągająca pomiędzy donorem i swobodnym elektronem. Do opisu takiego układu ( donor + swobodny elektron) możemy użyć przybliżenia masy efektywnej, gdzie elektron traktowany jest jak cząstka swobodna o masie
i ładunku -e . Energia kinetyczna elektronu będzie wówczas równa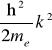
lub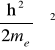
, potencjał donora jest równy odpowiednio
, gdzie
jest stałą dielektryczną materiału półprzewodnika. Zauważamy od razu ,że mamy tu do czynienia z problemem analogicznym do problemu atomu wodoru . Możemy użyć modelu Bohra lub bardziej ogólnego modelu kwantowego. W obu przypadkach otrzymujemy następujące wartości energii stanów stacjonarnych układu.

(IX-1)

W powyższym wzorze R jest stałą Rydberga. Dla wygody wprowadzono pojęcie stałej efektywnego Rydberga
. Ważnym parametrem jest promień Bohra , czyli promień orbity elektronu w stanie podstawowym

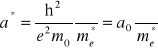
(IX-2)

Z powyższych rozważań wynika ,że wprowadzenie domieszek donorowych powoduje pojawienie się dodatkowych stanów w przerwie energetycznej, których energie liczone od dna pasma przewodnictwa dane są wzorem ( IX-1) . Parametrem , który określa głębokość tych stanów jest Rydberg efektywny. Dla typowych półprzewodników , dla których masa efektywna jest równa 0.1 m₀ , zaś stała dielektryczna jest równa ok. 10, stała Rydberga wynosi R=13.6 eV. Korzystając z (IX-1) otrzymamy R*=13.6meV. Jest to energia na tyle niewielka, że w temperaturze pokojowej większość donorów będzie zjonizowana. Nie mniej jednak w bardzo niskich temperaturach elektrony są związane z poszczególnymi donorami, zajmując obszar przestrzeni o promieniu równym
. Dla danych wartości masy efektywnej i stałej dielektrycznej efektywny promień Bohra wynosi
52.9 Å., czyli obejmuje wiele stałych sieci krystalicznej.

Przypadek akceptorów jest prawie całkowicie symetryczny. W modelu prawie swobodnych elektronów dziura znajdująca się w pasmie walencyjnym nie jest związana z żadnym konkretnym atomem. Jeśli dziura nie znajduje się blisko akceptora to jon akceptora ma efektywny ładunek równy -e. W rezultacie identycznie jak w przypadku elektronu i donora pojawia się siła przyciągająca pomiędzy dziurą i akceptorem. To oddziaływanie odpowiedzialne jest za pojawienie się stanów akceptorowych w przerwie energetycznej powyżej wierzchołka pasma walencyjnego. Ich energie liczymy identyczne jak przypadku donorów. O trzymujemy wartości energii

(IX-3)

Energie są dodatnie ponieważ stany leżą powyżej wierzchołka pasma walencyjnego. Podobnie jak poprzednio wprowadza się stałą efektywnego Rydberga
. Ważnym parametrem jest promień Bohra , czyli promień orbity dziury w stanie podstawowym

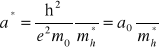
(IX-3)

W obu przypadkach wprowadzenie domieszek powoduje pojawienie się dodatkowych nośników ale i dodatkowych stanów w przerwie energetycznej. Schematycznie struktura energetyczna przedstawiona jest na rysunku (IX-1)

Stany donorowe E_d

E_g

Stany akceptorowe

E_a

Położenie poziomu Fermiego w półprzewodnikach domieszkowych.

Niezależnie od tego skąd się tam wzięły liczba elektronów w pasmie przewodnictwa,
, i liczba dziur pasmie walencyjnym,
dane są przez przybliżone wzory (VIII-29) i (VIII-30). Relacje te są więc również prawdziwe w przypadku półprzewodników domieszkowanych .

Rozważmy półprzewodnik, w którym znajdują się donory i akceptory o koncentracjach odpowiednio
i
oraz energiach liczonych względem dna pasma przewodnictwa i wierzchołka pasma walencyjnego równych odpowiednio
i
. Liczbę elektronów w pasmie przewodnictwa i dziur w pasmie walencyjnym możemy policzyć następująco:

(IX-4)

(IX-5)

W powyższych wzorach
i
są odpowiednio liczbami zjonizowanych donorów i akceptorów.
i
są liczbami nośników mniejszościowych. Nośniki te genrowane są w procesach termicznej kreacji par elektron -dziura. Nazwa mniejszościowe pojawia się aby odróżnić je od nośników dostarczanych przez domieszki zwanych nośnikami większościowymi . Zasada zachowania ładunku wymaga aby
=
. Powyższa relacja prowadzą do równania

(IX-6)

Liczbę zjonizowanych donorów i akceptorów można wyznaczyć biorąc pod uwagę, że obsadzenie stanów donorowych i akceptorowych dane jest przez statystykę Fermiego.

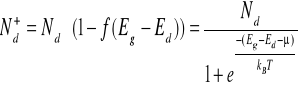
(IX-7)

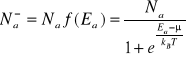
(IX-8)

Podstawiając relacje (IX-7), (iX-8) oraz (VIII-29) i (VIII-30) do równania (IX-6) otrzymujemy wyrażenie , z którego można obliczyć energię Fermiego,
. W ogólnym przypadku ma ono mało czytelną postać:

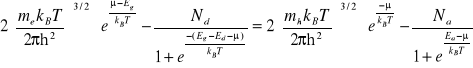
(IX-9)

Można przyjrzeć się bliżej dwóm granicznym przypadkom, półprzewodnika typu n, domieszkowanego donorami i półprzewodnika typu p domieszkowanego akceptorami. W przypadku półprzewodnika typu n możemy założyć , że liczba akceptorów równa się zeru. Równanie (IX-9) przyjmie postać:

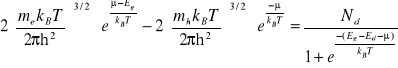
(IX-10)

Równanie to ma rozwiązanie tylko wówczas gdy poziom Fermiego leży w pobliżu dna pasma przewodnictwa. Można pominąć drugi składnik po lewej stronie równania ( IX-10). Otrzymuje się wówczas

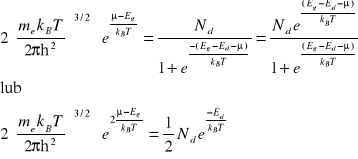
(IX-11)

Drugie równanie otrzymano zakładając, że dla odpowiednio wysokich temperatur można przyjąć
. Uproszczenie to nie jest niezbędne gdy analizuje się ilość elektronów w pasmie przewodnictwa, wygodnie jest jednak stosować ponieważ prowadzi go prostego analitycznego wyrażenia na energię Fermiego.

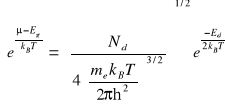
(IX-12)

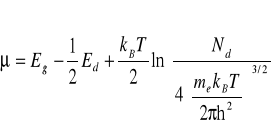
(IX-13)

Z równania (IX-13) widać, że w niskiej temperaturze energia Fermiego znajduję się mniej więcej w połowie pomiędzy dnem pasma przewodnictwa a poziomem donorowym. Wykorzystując równania (IX-11) otrzymujemy następujący wzór na koncentrację elektronów w pasmie przewodnictwa

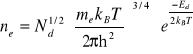
(IX-14)

Jak widać ilość elektronów w pasmie przewodnictwa jest proporcjonalna do pierwiastka kwadratowego z ilości donorów.

Przeprowadzając podobne rachunki można obliczyć położenie poziomu Fermiego w półprzewodniku typu p oraz odpowiednio koncentrację dziur. Odpowiednie zależności będą dane przez wzory.

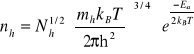
(IX-15)

oraz

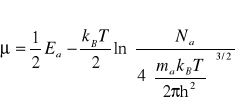
(IX-16)

Złącze p-n.

Znajomość położenia energii Fermiego w pasmie wzbronionym w półprzewodnikach typu p i typu n pozwala lepiej zrozumieć działanie złącza półprzewodnikowego. Jak pokazano poziom Fermiego w półprzewodniku typu n leży w pobliżu pasma przewodnictwa, a w półprzewodniku typu p w pobliżu pasma walencyjnego. Jeżeli połączymy ze sobą oba półprzewodniki energię Fermiego powinny się wyrównać. Powoduje to dyfuzję elektronów z półprzewodnika typu n do półprzewodnika typu p, i dziur z półprzewodnika typ p do półprzewodnika typu n. W wyniku tego powstaje tzw. potencjał zaporowy Półprzewodnik typu p będzie miał ładunek ujemny a półprzewodnik typu n ładunek dodatni . Pojawienie się potencjału zaporowego zobrazowane jest przez odpowiednie wygięcie pasm. (patrz rys IX-2 a).

Przy polaryzacji złącza (+) do n a (-) do p potencjał ten powiększa się i prąd nośników większościowych nie płynie (patrz rys IX-2 b). Taka polaryzacja nazywa się polaryzacją zaporową. Łatwo zauważamy , że przez złącze spolaryzowane w kierunku zaporowym płynie prąd nośników mniejszościowych.

Jeśli spolaryzuje się złącze kierunku przeciwnym ( -) do n (+) do p wówczas bariera potencjału ulegnie obniżeniu i zacznie płynąć prąd nośników większościowych ( patrz Rys. IX-2. c) .

Fig IX.-2 a Złącze niespolaryzowane

p n

● ● ●

●●●●●●●●●●●●

○○○○○○○○○○○○○○○

○ ○ ○

obszar przejściowy

Fig IX b złącze spolaryzowane zaporowo napięciem U₁

p n

● ● ●

○○○○○○○○○○○○○○○

●●●●●●●●●●●● U₁

○ ○ ○

Fig IX 2. c Złącze spolaryzowane w kierunku przewodzenia napięciem U₂

p n

● ● ●

●●●●●●●●●●●●

○○○○○○○○○○○○○○○ U₂

○ ○ ○

6

7

Pasmo przewodnictwa

Pasmo walencyjne

Rys. IX-1 Struktura pasmowa obsadzone przez elektrony jest pasmo walencyjne

---