Nr 20 + 30 = 50
Prawo Gaussa
Zad. 1
Szerokość dna rowu wynosi a=1,05 m z błędem średnim ma=0,2 m; głębokość
h= 2,05 m, mh=0,2 m, długość l=1050,00 m, ml=1m. Obliczyć objętość v tego rowu i jej błąd średni, jeżeli szerokość rowu w koronie jest równa b=3,05 m, mb= 0,2 m. Wskazać wielkość, której błąd średni ma największy wpływ na dokładność wyznaczenia objętości.
![]()
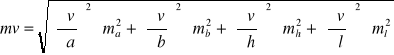
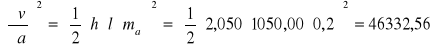
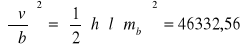
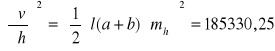
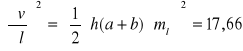
![]()
![]()
Błąd względny: ![]()
Odp.: Największy wpływ na wyznaczenie objętości rowu ma błąd pomiaru wysokości.
Zad. 2
Z jakim błędem średnim należy mierzyć kat c równy ok. 300, aby na podstawie tego kąta
i przyległych do niego boków a, b, można było obliczyć powierzchnię trójkąta z błędem średnim względnym równym 1/100. Przyjąć a=205.00 m, ma= 0,1 m, b=305,00 m, mb=0,1 m.
![]()
ms2=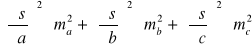
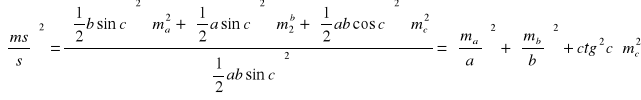
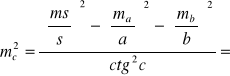
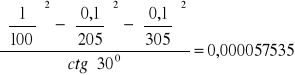
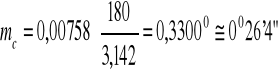
Odp.: Aby średni błąd względny powierzchni mierzonego trójkąta nie przekroczył 1/100 błąd średni pomiaru kąta może wynosić 00 26'4”.
Zad. 3
Z jakim średnim błędem względnym należy pomierzyć boki a,b prostokąta, aby można było wyznaczyć powierzchnię s tego prostokąta z średnim błędem względnym ms/s=1/200 .
![]()
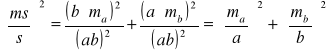
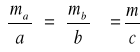
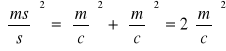
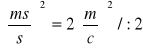
![]()
![]()
![]()
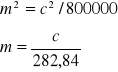
Zad. 4
Długość boku poligonowego w terenie wynosi l=150.00 m, a jego błąd średni 0,05 m. Przyjmując, że kąt nachylenia tego boku do poziomu ![]()
pomierzono z błędem średnim ![]()
. Wyznaczyć błąd średni długości l0 tego boku zredukowanej do poziomu.
![]()
![]()
![]()
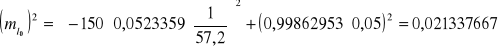
![]()
0,15
Odp. Błąd średni zredukowanej długości l0 wynosi 0,15 m.
Zad. 5
Z jaką dokładnością należy pomierzyć kąty nachylenia linii pionu od poziomu, w terenie o maksymalnym spadku 50, aby błąd średni 0długości zredukowanej spowodowany błędem pomiaru nachylenia nie przekraczał 2 cm dla odcinka 150 m.
![]()
![]()
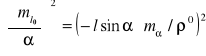
![]()
![]()
![]()
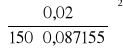
=0,000000000135
![]()
=0000'2”,39
Odp.: Aby błąd średni długości zredukowanej nie przekraczał 2 cm dla odcinka 150 m przy nachyleniu 50 , błąd pomiaru kąta nie może przekraczać 000'2”,39
Wyszukiwarka