„Wahadło”
Plan sprawozdania
Opis doświadczenia
Rysunek
Przykładowe wyliczenia
Tabela pomiarów
Wykresy
Dyskusja błędów pomiarowych
Wnioski
Jacek Gwóźdź
1. Opis doświadczenia
Kolejne etapy doświadczenia:
1. Zawieszam ciężarek na cienkiej nici.
2. Całość zawieszam na statywie.
3. Za pomocą metra mierniczego odmierzam kolejne odległości ( 7 pomiarów) od punktu zawieszenia wahadła do środka ciężkości ciężarka.
4. Notuję 3 razy na daną długość wahadła czasy 10 wahnięć ciężarka.
4. Wyniki notuję na specjalnie przygotowanej tabelce.
5. Obliczamy g z powyższego wzoru.
6. Sprawdzamy czy otrzymane wyniki są zbliżone do rzeczywistych.
7. Przeprowadzenie dyskusji niepewności pomiarowych.
8. Wyliczenie gśrednie dla całego doświadczenia.
9. Wnioski końcowe.
Celem doświadczenia „Wahadło” jest eksperymentalne sprawdzenie teorii ruchu wahadła matematycznego, a także obliczenie wartości przyspieszenia ziemskiego. Wahadłem matematycznym nazywamy ciężarek o małych rozmiarach zawieszony na cienkiej nici, który może się wahać. Dla rozważań nad ruchem wahadła możemy przyjąć, że wahadło matematyczne to małe ciało - punkt materialny umieszczony na nierozciągliwej i nieważkiej nici o długości l. W rzeczywistości jednak możemy zrealizować wahadło matematyczne tylko w przybliżeniu. Dzieje się tak, ponieważ nie możemy zredukować wymiarów ciężarka do punktu materialnego. Dla uzyskania jak najmniejszych drgań i w konsekwencji jak najdokładniejszych pomiarów wychylaliśmy je na kąt α<5○. Dzięki prawom mechaniki na okres drgań wahadła matematycznego oraz wzorowi na przyspieszenie ziemskie:
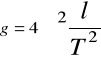
Wyniki doświadczenia oraz powyższy wzór przyczyniły się do tego, że mogłem obliczyć przyśpieszenie ziemskie. Ze względu na niedokładność ludzkiego oka przyjąłem błąd przy mierzeniu długości wynoszący 5mm = 0,005m.
2. Rysunek
3. Przykładowe obliczenia
Obliczenia dla pomiaru numer 1.

Obliczanie końcowego g dla doświadczenia
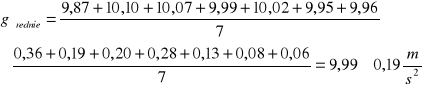
4.Tabela pomiarów
Nr |
l [m] |
Δl [m] |
10T[s] |
10 |
|
ΔTmax [s] |
g [m/s2] |
Δg [m/s2] |
1. |
0,25 |
0,005 |
1. 10,02 |
9,96 |
1,00 |
0,008 |
9,87 |
0,36 |
|
|
|
2. 9,86 |
|
|
|
|
|
|
|
|
3. 10,00 |
|
|
|
|
|
2. |
0,4 |
0,005 |
1. 12,53 |
12,49 |
1,25 |
0,004 |
10,10 |
0,19 |
|
|
|
2.12,49 |
|
|
|
|
|
|
|
|
3. 12,46 |
|
|
|
|
|
3. |
0,5 |
0,005 |
1. 14,01 |
13,99 |
1,40 |
0,007 |
10,07 |
0,20 |
|
|
|
2. 14,05 |
|
|
|
|
|
|
|
|
3. 13,92 |
|
|
|
|
|
4. |
0,6 |
0,005 |
1. 15,61 |
15,42 |
1,54 |
0,015 |
9,99 |
0,28 |
|
|
|
2. 15,33 |
|
|
|
|
|
|
|
|
3. 15,32 |
|
|
|
|
|
5. |
0,7 |
0,005 |
1. 16,54 |
16,57 |
1,66 |
0,005 |
10,02 |
0,13 |
|
|
|
2. 16,54 |
|
|
|
|
|
|
|
|
3. 16,63 |
|
|
|
|
|
6. |
0,9 |
0,005 |
1. 18,85 |
18,85 |
1,89 |
0,002 |
9,95 |
0,08 |
|
|
|
2. 18,87 |
|
|
|
|
|
|
|
|
3. 18,84 |
|
|
|
|
|
7. |
1 |
0,005 |
1. 19,90 |
19,89 |
1,99 |
0,001 |
9,96 |
0,06 |
|
|
|
2. 19,88 |
|
|
|
|
|
|
|
|
3. 19,88 |
|
|
|
|
|
Wynik końcowy: g =9,99![]()
[m/s2]
5. Wykresy
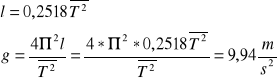
6. Dyskusja błędów pomiarowych
Błędy pomiarowe wynikają z:
Nieidealnego zsynchronizowania czasu włączania i wyłączania stopera i wprowadzania w ruch wahadła
Niedokładności mierzenia długości nici
Nie uwzględnieniu siły oporu powietrza i tarcia między nicią, a statywem
Wprowadzenie drgań bocznych podczas wprawiania w ruch wahadło
Dla uzyskania idealnych warunków doświadczenie to powinno wykonywać się w próżni i najlepiej za pomocą dokładnych maszyn
7. Wnioski
Dzięki takiemu doświadczeniu możemy zaobserwować jak w prosty sposób możemy obliczyć przybliżoną wartość przyspieszenia ziemskiego, i w jakie jest działanie wahadła matematycznego. Dowiedzieliśmy się także, że dokładność w doświadczeniach bardzo ważna i to od niej zależy końcowy wynik pracy.
2
Wyszukiwarka