WYZNACZNIKI
Każdej macierzy KWADRATOWEJ przyporządkujemy LICZBĘ zwaną wyznacznikiem tej macierzy.
Umowa. O wyznaczniku macierzy wymiaru n x n mówimy, że jest to wyznacznik stopnia n.
Oznaczenia. Jeżeli macierz oznaczymy literą, np. A, to wyznacznik tej macierzy oznaczymy: det A (od słowa „determinant”).
Jeżeli macierz nie jest nazwana, ale zapisana jako tablica liczb np. 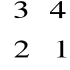
, to jej wyznacznik zapiszemy tak: 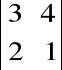
Wyznacznik stopnia 1 Jeżeli ![]()
, to ![]()
Wyznacznik stopnia 2
Jeżeli 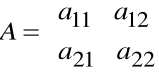
, to ![]()
Przykład 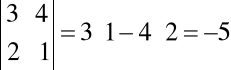
Zadanie. Oblicz wyznaczniki: 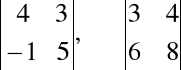
Minor elementu wyznacznika
Minorem elementu ![]()
wyznacznika W nazywamy wyznacznik, który powstaje z wyznacznika W przez skreślenie w nim wiersza nr i oraz kolumny nr j.
Minor elementu ![]()
oznaczamy: ![]()
Przykład. Rozważmy wyznacznik 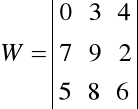
Liczba 2 to element ![]()
. Minor tego elementu 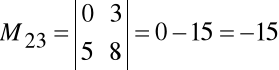
Liczba 3 to element ![]()
; minor tego elementu
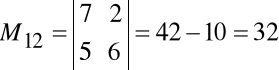
itd.
Zadanie. Oblicz (dla powyższego wyznacznika) ![]()
oraz ![]()
Wyznacznik stopnia 3
Jeżeli 
, to
![]()
Powyższy wzór nazywamy rozwinięciem wyznacznika według pierwszego wiersza.
Przykład.
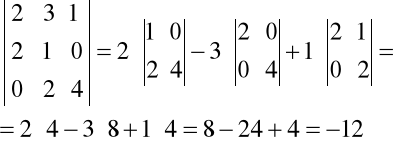
Zadanie. Oblicz wyznaczniki: 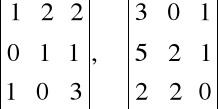
Wyznacznik dowolnego stopnia
Jeżeli 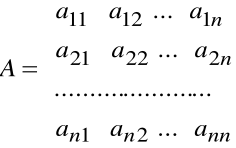
, to
![]()
W powyższym wzorze znaki układają się na przemian: ![]()
Przykład.
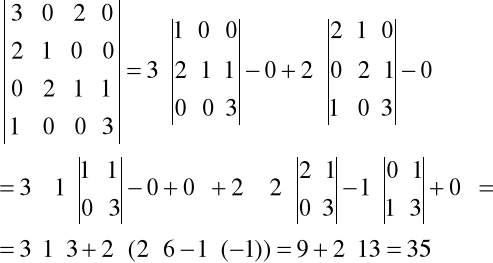
Zadanie. Oblicz wyznacznik: 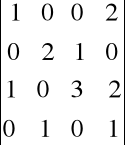
Rozwinięcie wyznacznika według dowolnego wiersza
Wyznacznik możemy rozwijać według dowolnego wiersza a także według dowolnej kolumny, z tym, że:
- jeżeli numer wiersza lub kolumny jest nieparzysty, to znaki we wzorze na rozwinięcie występują w kolejności: ![]()
- jeżeli numer wiersza lub kolumny jest parzysty, to znaki we wzorze na rozwinięcie występują w kolejności: ![]()
Przykład. Obliczymy wyznacznik: 
Najkorzystniej będzie rozwinąć go według kolumny nr 4, gdyż zawiera ona najwięcej zer:
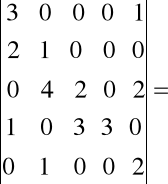
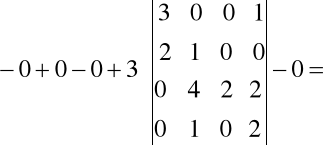
={skorzystamy z kolumny nr 3}= 
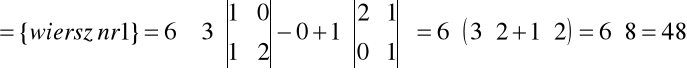
Zadanie. Kilkoma sposobami oblicz wyznacznik: 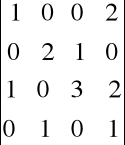
Twierdzenia o wyznacznikach
1. Jeżeli w wyznaczniku istnieje wiersz lub kolumna samych zer, to ten wyznacznik jest równy zero.
2. Jeżeli w wyznaczniku istnieją dwa identyczne wiersze lub dwie identyczne kolumny, to ten wyznacznik jest równy zero.
3. Jeżeli w wyznaczniku pod przekątną główną lub nad przekątną główną znajdują się same zera, to ten wyznacznik jest równy iloczynowi wyrazów z głównej przekątnej, np. 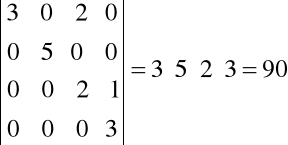
4. Jeżeli w wyznaczniku zamienimy miejscami dwa wiersze lub dwie kolumny, to wartość wyznacznika zmieni się na przeciwną np. 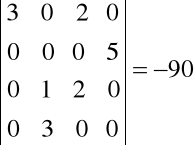
5. Jeżeli wyznacznik ma wartość p i jeden wiersz lub jedną kolumnę tego wyznacznika pomnożymy przez liczbę k, to otrzymany wyznacznik ma wartość k∙p
6. Jeżeli w wyznaczniku do wiersza dodamy inny wiersz pomnożony przez liczbę, to wartość wyznacznika nie zmieni się. To samo dotyczy kolumn.
Własność 6 jest przydatna przy obliczaniu wartości wyznaczników, w których jest mało zer.
Przykład. Obliczmy 
Wykonamy następujące operacje:
- wiersz nr 1 (w1) bez zmian,
- ![]()
- ![]()
- ![]()

=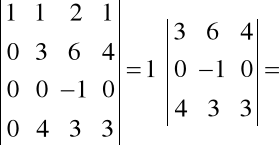
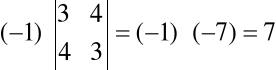
Zadanie. Oblicz wyznaczniki: 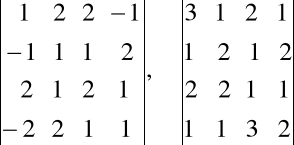
Wyszukiwarka