Treść zadania
Włoska firma LA PASTA zamierza zaistnieć na polskim rynku. Zamierza ona zakupić maszynę od polskiego producenta, która jest w stanie wyprodukować w ciągu miesiąca 3000kg makaronu świderek lub 1500kg makaronu muszelek. Jednak producent sugeruje, iż w dłuższym okresie pracy maszyna powinna produkować nie mniej niż 500kg świderek i 450kg muszelek i nie więcej niż 1300kg świderek i 2800kg muszelek. Norma zużycia mąki w maszynie wynosi na kilogram makaronu świderek 0,85 kilograma, a makaronu muszelek 0,9 kilograma. Przedsiębiorstwo co miesiąc otrzymuje dostawę 2 ton specjalnej mąki. Oprócz mąki do produkcji przedsiębiorstwo zużywa także jaja, 2 jajka na kg świderek i 3 jajka na kg muszelek. Przedsiębiorstwo ma podpisaną umowę na dostawę 4160 jajek miesięcznie. Oszacowano, że zyski za kg wynoszą 2,5 zł. w przypadku świderek i 2,9 zł. dla muszelek. Opłacalność produkcji zapewni zysk powyżej 3000zł. Przy jakiej strukturze produkcji przedsiębiorstwo osiągnie najwyższy zysk?
Pytania dodatkowe
1. LA PASTA podejmując działania promocyjne postanowiła obniżyć cenę świderek do 2 zł, a muszelek do 2, 50zł. Jak ta zmiana wpłynie na optymalną strukturę produkcji?
2. Jak zmieni się wartość funkcji celu, gdyby z powodu nieurodzaju zmniejszyła się dostawa mąki o 400 kg?
3. Z powodu opóźnienia dostawy, dostawca jaj w ramach „przeprosin” dostarczył 5000 jaj. Jak wówczas zmieni się wartość zysku firmy LA PASTA?
4. Optymistyczne przewidywania producenta maszyny dotyczące jej wydajności były mylne. Okazało się, że maszyna nie może produkować więcej niż 1200 świderek i 2500 muszelek. Jak ta sytuacja wpłynie na wartość zysku?
Rozwiązanie zadania
Dane dotyczące przedsiębiorstwa LA PASTA
|
ŚWIDERKI |
Muszelki |
||
Wydajność |
3000 kg na m-c |
1500 kg na m-c |
||
Zalecenia producenta |
Minimum 500 kg na m-c |
Maximum 1300 kg na m-c |
Minimum 450 kg na m-c |
Maximum 2800 kg na m-c |
Tabela 1 - możliwości produkcyjne zakupionej maszyny
|
Świderki |
Muszelki |
Zużycie mąki na kg makaronu |
0,85 |
0,90 |
Zużycie jajek na kg makaronu |
2 |
3 |
Tabela 2 - zużycie surowców do produkcji makaronu
Zmienne decyzyjne
s - wielkość produkcji makaronu świderek
m - wielkość produkcji makaronu muszelek
Warunki ograniczające
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
Opisy ograniczeń
Przedstawia wydajność maszyny w ciągu jednego miesiąca.
Dotyczy minimalnej produkcji świderek sugerowanej przez producenta maszyny.
Dotyczy maksymalnej produkcji świderek sugerowanej przez producenta maszyny.
Dotyczy minimalnej produkcji muszelek sugerowanej przez producenta maszyny.
Dotyczy maksymalnej produkcji muszelek sugerowanej przez producenta maszyny.
Przedstawia zużycie mąki potrzebnej do produkcji makaronu.
Przedstawia zużycie jaj potrzebnych do produkcji makaronu.
Opisuje wysokość zysku przedsiębiorstwa zapewniającego opłacalność produkcji.
Wielkość produkcji świderek i wielkość produkcji muszelek nie może być ujemna.
Funkcja celu
![]()
Celem naszego badania jest osiągnięcie takiej struktury produkcji, przy której maksymalizujemy zysk.
ANALIZA WRAŻLIWOŚCI |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Wartości przedziału |
|
|
|||
Zmienna |
Wartość |
Koszt wejścia |
dla współczynników funkcji celu |
|
|
|||
|
|
|
Dolna |
Bieżąca |
Górna |
|
|
|
s |
1300,00 |
0,00 |
1,93 |
2,50 |
M |
|
|
|
m |
520,00 |
0,00 |
0,00 |
2,90 |
3,75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wartości przedziału |
|||
Ograniczenie Poziom w relacji do " =" |
Cena dualna |
dla ograniczenia |
||||||
|
|
|
|
|
Dolna |
Bieżąca |
Górna |
|
1) |
s+2m<=3000 |
|
|
|
|
|
||
|
MNIEJSZY |
SW_1 = 660,0001 |
0,00 |
2340,00 |
3000,00 |
M |
||
2) |
s>=500 |
|
|
|
|
|
|
|
|
WIĘKSZY |
SW_2 = 800 |
0,00 |
-M |
500,00 |
1300,00 |
||
3) |
m>=450 |
|
|
|
|
|
|
|
|
WIĘKSZY |
SW_3 = 69,99996 |
0,00 |
-M |
450,00 |
520,00 |
||
4) |
s<=1300 |
|
|
|
|
|
|
|
|
DOKŁADNY |
SW_4 = 0 |
|
0,57 |
500,00 |
1300,00 |
1405,00 |
|
5) |
m<=2800 |
|
|
|
|
|
|
|
|
MNIEJSZY |
SW_5 = 2280 |
0,00 |
520,00 |
2800,00 |
M |
||
6) |
0.85s+0.9m<=2000 |
|
|
|
|
|
||
|
MNIEJSZY |
SW_6 = 427 |
0,00 |
1573,00 |
2000,00 |
M |
||
7) |
2s+3m<=4160 |
|
|
|
|
|
||
|
DOKŁADNY |
SW_7 = 0 |
|
0,97 |
3950,00 |
4160,00 |
5150,00 |
|
8) |
2.5s+2.9m>3000 |
|
|
|
|
|
||
|
WIĘKSZY |
SW_8 = 1758 |
0,00 |
-M |
3000,00 |
4758,00 |
||
Interpretacja otrzymanych wyników
Interpretacja zmiennej s:
Wielkość tej zmiennej opisuje optymalną produkcję makaronu świderek przy danych w zadaniu parametrach. Wnioskujemy z tego, że przedsiębiorstwo maksymalizuje swoje zyski przy produkcji 1300 kilogramów świderek na miesiąc.
Interpretacja zmiennej m:
Zmienna ta dotyczy optymalnej produkcji makaronu muszelek przy danych w zadaniu warunkach. Zmienna m wynosi 520, więc przedsiębiorstwo maksymalizuje zysk przy produkcji 520 kilogramów muszelek w ciągu miesiąca.
Interpretacja zmiennej s1:
Wyprodukowano w sumie 660 kilogramów makaronu mniej, niż pozwala na to maksymalne wykorzystanie zdolności produkcyjnych maszyny.
Interpretacja zmiennej s2:
Przedsiębiorstwo w optymalnej sytuacji produkuje o 800 kilogramów świderek więcej niż zakładał minimalnie producent maszyny.
Interpretacja zmiennej s3:
Przedsiębiorstwo produkuje w optymalnej sytuacji o 70 kilogramów więcej muszelek niż zakładało minimum postawione przez producenta maszyny.
Interpretacja zmiennej s4:
Przedsiębiorstwo w optymalnej sytuacji produkuje dokładnie tyle świderek ile sugerował maksymalnie producent maszyny.
Interpretacja zmiennej s5:
Przedsiębiorstwo produkuje o 2280 kilogramów muszelek mniej niż wynosił maksymalny poziom produkcji muszelek sugerowany przez producenta maszyny.
Interpretacja zmiennej s6:
Przy produkcji maksymalizującej zysk (1300 kilogramów świderek i 520 kilogramów muszelek) zostaje wykorzystane o 427 kilogramów mąki mniej niż wynoszą miesięczne dostawy.
Interpretacja zmiennej s7:
Przedsiębiorstwo podczas optymalnej produkcji zużywa dokładnie tyle jajek ile wynoszą dostawy (4160 jaj).
Interpretacja zmiennej s8:
Produkując 1300 kilogramów świderek i 520 kilogramów muszelek przedsiębiorstwo osiągnie o 1758 PLN więcej niż zakładano minimalnie.
Przedsiębiorstwo przy optymalnej produkcji osiągnie zysk w wysokości 4758 zł.
Odpowiedzi na pytania dodatkowe
Obniżenie ceny świderek do 2zł, a ceny muszelek do 2,50zł nie zmieni optymalnej struktury produkcji (przedsiębiorstwo nadal będzie produkowało 1300 kg świderek i 520 kg muszelek), gdyż wartości nowych cen mieszczą się w przedziale wartości dla współczynników funkcji celu, w którym koszt wejścia wynosi 0. Natomiast zysk łączny zmaleje o 858 zł (gdyż
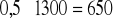
zł, a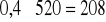
) i będzie wynosił 3900zł.W przypadku zmniejszenia dostaw mąki o 400kg wartość funkcji zysku nie zmieniłaby się, gdyż w procesie produkcyjnym (przy optymalnej strukturze produkcji) nie wykorzystujemy 427 kg mąki (o czym mówi nam zmienna s6 ). Niewykorzystanych pozostanie jeszcze 27 kg mąki.
Dostawa składająca się z 5000 jaj wpłynie na zysk przedsiębiorstwa LA PASTA zwiększając go o 814,80 zł (dostawa zwiększyła się o 840 sztuk jaj, mieścimy się w wartościach przedziału dla ograniczenia, gdzie cena dualna wynosi 0,97 zł, stąd
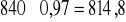
zł). Łączny zysk będzie wynosił 5572,8 zł.
Pomyłka producenta maszyny obniży łączny zysk z produkcji obu rodzajów makaronu w następujący sposób:
zmniejszając maksymalny poziom produkcji świderek do 1200kg zysk obniży się o 57 zł (gdyż 1200kg mieści się w wartościach przedziału dla ograniczenia, gdzie cena dualna wynosi 0,57zł, stąd
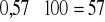
zł).
Zmniejszenie maksymalnego poziomu produkcji muszelek do 2500kg nie wpłynie na wartość zysku (gdyż w procesie produkcyjnym przy optymalnej strukturze produkcji nie jest wytwarzanych 2280kg muszelek, o czym mówi nam zmienna s5).
Stąd, łączny zysk zmniejszy się o 57zł i będzie wynosił 4701zł.
Praca pochodzi z serwisu www.e-sciagi.pl
Wyszukiwarka