nr ćw. 109 |
Data 23.III. 2000 |
Łukasz Durzewski |
Wydział Elektryczny |
Semestr II |
Grupa E3 Nr lab 8
|
Prowadzący : Tomasz Runka
|
przygotowanie |
wykonanie |
ocena końcowa |
||
Temat: Badanie ruchu jednostajnie zmiennego
Wiadomości podstawowe.
Ruch zmienny
Punkt materialny (ciało posiadające masę lecz nie posiadające objętości) poruszając się w jednowymiarowym układzie współrzędnych tak, że oś x pokrywa się z torem ruchu , to współrzędna x tego punktu jest funkcją czasu x=x(t).
Jeżeli w chwili t0 współrzędna punktu wynosi x0, zaś w chwili t wynosi x , to prędkość średnia vśr punktu wynosi:
![]()
(1)
Jeżeli dla danego punktu wartość prędkości v jest stała dla wszystkich wartości t i t0 tzn. nie zależy ani od chwili początkowej ani od odstępu czasu, dla którego została wyznaczona, wówczas mówimy o ruchu jednostajnym. Jeśli ten ruch odbywa się po linii prostej wtedy mówimy o ruchu jednostajnym prostoliniowym.
Wszystkie pozostałe rodzaje ruchów nazywamy zmiennymi niezależnie od kształtu ich toru. Wielkościami charakteryzującymi ruch zmienny są :
Prędkość średnia (analogicznie jak w przypadku ruchu jednostajnego z wyjątkiem oznaczeń t=t-t0, Δx=x-x0)
![]()
(2)
Prędkość chwilowa (rzeczywista) mówimy wtedy gdy prędkość średnia jest wielkością zmienną, wartość prędkości wyraża się wzorem:
![]()
(3)
Prędkość chwilowa jest więc pochodną drogi po czasie4)
![]()
(4)
Jednostką prędkości w układzie SI jest m/s
Droga jaka została przebyta w określonym czasie może zostać obliczona przez scałkowanie przekształconego (3).który teraz ma postać:
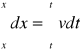
czyli 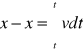
(5)
Ponieważ v=const., otrzymujemy
x-x0=v(t-t0)
(6)
Dla ruchu o stałej prędkości, droga przebyta w czasie t jest proporcjonalna do czasu, prędkość zaś jest współczynnikiem proporcjonalności,
Przyspieszenie.
Przyspieszenie występuje wtedy gdy i prędkość nie jest stał na określonym przyroście drogie i w określonym przyroście czasu. Wartość przyspieszenia średniego określona jest wzorem:
![]()
(7)
O przyspieszeniu chwilowym (rzeczywistym ) mówimy wtedy gdy przyspieszenie średnie jest wielkością zmienną. Wartość ta wyraża się wzorem
![]()
(8)
Przyspieszenie rzeczywiste jest więc pochodną prędkości względem czasu:
![]()
(9)
Jednostką przyspieszenia w układzie SI jest m/s2.
Ruchem w którym przyspieszenie jest wartością stałą nazywamy ruchem jednostajnie przyspieszonym gdy a>0 lub jednostajnie opóźnionym gdy a<0. Wartości charakteryzujące ten ruch to prędkość oraz droga.
Prędkość
Wartość prędkości można wyznaczyć przez przekształcenie i scałkowanie wzoru (9):
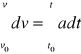
(10)
dla a =const:
v-v0=a(t-t0)
(11)
dla t0=0 otrzymujemy
v=at+v0
(12)
Wykresem prędkości jako funkcji czasu (rys.1) jest linia prosta A b nachylona do soi czasu pod kątem α takim, że tg(α)=a i przecinającą oś v w punkcie v0. Wielkość v0 jest prędkością początkową, jaką ma ciało w chwili rozpoczęcia ruchu.
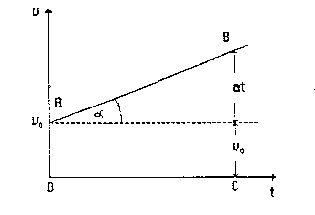
Rys 1 Wykres prędkości w ruchu jednostajnie zmiennym
Droga
Z równania (4) oraz (12) wynika ,że
dx=vdt=(v0+at)dt
(13)
Całkując obie strony równania (13)
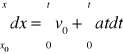
(14)
otrzymujemy
![]()
(15)
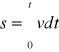
Ogólnie, jeżeli krzywa AB (rys.2) przedstawia wykres prędkości jako funkcji czasu w dowolnym ruchu zmiennym po linii prostej, wówczas powierzchnia
(16)
Zatem pole OABC jest równe drodze przebytej przez to ciało w czasie t.
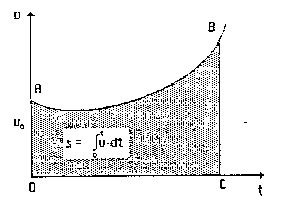
Rys.2 droga w ruchu zmiennym
Swobodny spadek
Szczególnym przypadkiem ruchu jest tzw. swobodny spadek, jest to ruch z prawie stałym przyspieszeniem. Stwierdzono, że gdy nie występują opory powietrza, wszystkie ciała niezależnie od ich rozmiarów, ciężaru i składu chemicznego spadają z takim samym przyspieszeniem ziemskim „g” równym przy powierzchni ziemi 9,81 m/s2.
Do opisu spadku swobodnego stosujemy równanie
v=gt+v0 ![]()
(17 i 18)
Dla ruchu bez prędkości początkowej v0 oraz x0 powyższe równania mają postać:
v=gt ![]()
(19 i 20)
Tarcie
Zjawisko towarzyszące względnemu przemieszczani dociśniętych do siebie lub stykających się dwóch różnych ciał (tzw. zewnętrzne) lub elementów tego samego ciała (tzw. wewnętrzne). Według sposobu przemieszczania się ciała rozróżnia się :
tarcie ślizgowe
tarcie toczne
tarcie wiertne
Ze względu na prędkość względną ciał trących dzieli się tarcie na:
tarcie spoczynkowe ( statyczne) wyrażające się siłą, którą trzeba przyłożyć, aby wprawić ciało w ruch. Stosunek maksymalnej wartości siły tarcia statycznego do wartości siły normalnej nazywamy współczynnikiem tarcia statycznego
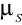
dla danych powierzchni:
![]()
(21)
gdzie N- wartość bezwzględna siły normalnej. Znak równości odnosi się do przypadku, gdy TS ma maksymalną wartość.
tarcie ruchowe (kinetyczne) odpowiadające sile, którą trzeba pokonać, aby te ciało utrzymać w ruchu. Stosunek wartości siły tarcia kinetycznego do wartości siły normalnej N nazywamy współczynnikiem tarcia kinetycznego, gdzie FK to wartość bezwzględna siły tarcia kinetycznego
![]()
(22)
μS i μK są stałymi bezwymiarowymi. Zwykle da danej pary powierzchni μS>μK. Rzeczywista wartość μS i μK zależy od rodzaju stykających się powierzchni. Wartość tych współczynników na ogół jest mniejsza od 1.
Mierząc przyspieszenie „a” staczającego się wózka po równi pochyłej pod wpływem składowej stycznej „S” jego ciężaru i siły hamującej wywołanej ciężarem przeciwwagi „P” oraz siły tarcia „T” na podstawie drugiej zasady możemy napisać równanie ruchu
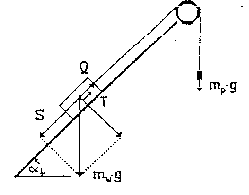
S-Q-T=a(mW+mP)
(23)
Rys 3 Schemat pomiarowy
Po podstawieniu S=mWg sin(α) i Q= m.Pg i przekształceniu otrzymujemy:
T=mWgsin(α)-m.pg-a(mW+m.P)
(24)
gdzie m.W i mP -masy wózka i przeciwwagi .
Przebieg ćwiczenia
Wyznaczanie przyspieszenia ziemskiego.
Włączyć interfejs pomiarowy i komputer. Wywołać program Science Worshop i z menu PLIK otworzyć DRABINKA.SWS
Nacisnąć przycisk [ZAPISZ] lub [Alt + R] a następnie spuścić drabinkę przez bramkę świetlną. Drabinka powinna spadać na miękkie podłoże(np. gąbkę)
Po zakończeniu cyklu pomiarowego nacisnąć przycisk [STOP] lub [Alt + . (kropka)]. Program wyświetli wynik pomiaru przyspieszenia ziemskiego w tabeli.
Odpowiednio przeciągając kolumnę wyników, wybrać zakres w którym mieszczą się wartości zbliżone do oczekiwanych . Kilka pierwszych morze znacznie różnić się od wartości oczekiwanej, co jest spowodowane niewłaściwym początkowym ustawieniem drabinki.
Odczytać z pola statystyki wartość średnią i odchylenie standardowe.
Pomiar powtórzyć co najmniej 10 razy. Wyniki podać jako średnią arytmetyczną wszystkich pomiarów. Przeprowadzić dyskusje błędów. Przed każdym nowym pomiarem skasować poprzednią serię pomiarów. Po zakończeniu pomiarów zamknąć okno ustawienia ćwiczenia naciskając klawisz [Alt+W]
Wyznaczenie przyspieszenia na równi pochyłej
Z PLIKU otworzyć plik RÓWNIA.SWS
Równię pochyłą ustawić pod kątem 250. Nić obciążyć masą Mp= 130g. Przesunąć wózek na górę równi pochyłej i przytrzymać go w pozycji . Nacisnąć przycisk [ZAPISZ] lub [Alt+R] zwolnić wózek po upływie 1 sekundy. Zbyt mocne wahania przeciw wagi w czasie ruchu wózka obniżają dokładność pomiaru.
Po zakończeniu cyklu pomiarowego nacisnąć przycisk [STOP] lub [Alt + . (kropka)]. Wyniki pomiaru zostaną wyświetlone w postaci wykresu jako zależność v(t).
Przeciągając myszką, wybrać obszar wykresu odpowiadający ruchowi jednostajnie przyspieszonemu. Odchylenia od tego ruchu związane są z rozbiegiem (początek wykresu) i hamowaniem (koniec wykresu).
Z pola statystyka odczytać przyspieszenie .
Powtórzyć pomiar dla dodatkowego obciążenia wózka ( masa wózka bez dodatkowego obciążenia wynosi 350g) oraz kąt nachylenia równi 250.
Dla każdego pomiaru obliczyć siłę tarcia T wg wzoru ( 24)
Naciskając [Alt+Q] wyjść z programu bez zapisywania zmian
Obliczenia
Wyznaczanie przyspieszenia ziemskiego.
Pomiary zostały dokonanie za pomocą interfejsu komputerowego oraz programu który automatycznie zliczał wartość średnią dokonanych przez siebie pomiarów oraz odchylenie standardowe z dokonanej serii pomiarów . Wyniki pomiarów zostały przedstawione w tabeli 1.
Liczba pomiarów |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Średnia wartość przyspieszenia ziemskiego [m/s2] |
9,6074 |
9,7455 |
9,6258 |
9,8003 |
9,8494 |
9,7701 |
9,8509 |
9,7663 |
9,7339 |
9,6797 |
Odchylenie standardowe |
± 0,4273 |
± 0,7488 |
± 0,3757 |
± 0,6488 |
± 0,2543 |
± 0,3801 |
± 0,2477 |
± 0,2501 |
± 0,3007 |
± 0,5374 |
(tabela 1)
Z dokonanej serii pomiarów można obliczyć średnią arytmetyczną oraz odchylenie standardowe.
Średnia wartość przy. Ziem. z 10 pomiarów [m/s2] |
9,743 |
Odchylenie standardowe |
± 0,084 |
(tabela 2)
Obliczenia siły tarcia
Dane:
Masa wózka 350 [g] = 0.35 [kg]
Masa przeciwwagi 130[g] = 0.13 [kg]
Dodatkowe obciążniki 10, 20, 50 [g] = 0.01, 0.02, 0,05 [kg]
Przyspieszenie ziemskie 9,81 [m/s2]
Kont nachylenia równi 250
Obliczenia dla nieobciążonego wózka
Liczba pomiarów |
Przyspieszenie [m/s2] |
1 |
0,27222 |
2 |
0,25394 |
3 |
0,29237 |
wartość średnia |
0,273 |
odch.stand. |
±0,019 |
Obliczam tarcie stosując wzór (24)
Tarcie [N] |
0,045 |
Obliczenia dla wózka obciążonego dodatkowym obciążnikiem (0.01[kg])
Liczba pomiarów |
Przyspieszenie [m/s2] |
1 |
0,363682 |
2 |
0,367691 |
3 |
0,370261 |
wartość średnia |
0,367 |
odch. stand. |
± 0,003 |
Obliczam tarcie stosując wzór (24)
Tarcie [N] |
0,037 |
Obliczenia dla wózka obciążonego dodatkowym obciążnikiem (0.02[kg])
Liczba pomiarów |
Przyspieszenie [m/s2] |
1 |
0,44338 |
2 |
0,44627 |
3 |
0,441287 |
Wartość średnia |
0,445 |
Odch. stand. |
± 0,0025 |
Obliczam tarcie stosując wzór (24)
Tarcie [N] |
0,037 |
Obliczenia dla wózka obciążonego dodatkowym obciążnikiem (0.05[kg])
Liczba pomiarów |
Przyspieszenie [m/s2] |
1 |
0,65649 |
2 |
0,65102 |
3 |
0,65718 |
wartość średnia |
0,655 |
odch.stand. |
± 0,0034 |
Obliczam tarcie stosując wzór (24)
Tarcie [N] |
0,036 |
Wnioski
Wartość obliczona nieznacznie różni się od wartość przyspieszenia ziemskiego przyjmowanego do obliczeń ( 9.81 [m/s2]). Ta niewielka różnica w wynikach może być spowodowana faktem złego doboru wyników z tabeli pomiarowej, w której znalazły się wartość przyspieszenia ziemskiego odbiegające znacznie od wartości przyjmowanej do obliczeń. Wyniki te są konsekwencją złego początkowego ustawienia drabinki.
Jak widać z przedstawionych wyników wraz ze wzrostem obciążenia siła tarcia maleje. Dzieje się tak dlatego, że wartość składowej „S” (patrz rys 3) wzrasta wraz ze wzrostem masy wózka. Wzrost ten jest jednak nieznaczny do wzrostu przyspieszenia jakie jest wywołane wspólną masy wózka i przeciwwagi. W tym przypadku skorzystaliśmy z bilansu sił i nie uwzględniliśmy współczynnika chropowatości powierzchni. Z powodu na wysoką klasę dokładności urządzenia pomiarowego (interfejsu oraz komputera) błędy są znikome. Jedyny błąd mógł powstać przy obliczaniu średniej arytmetycznej przyspieszenia, błąd ten został obliczony z odchylenia standardowego. Wartość tego błędu została umieszczona w tabeli.
1
7
![]()
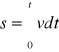
Wyszukiwarka