WYDZIAŁ MECHANICZNY TECHNOLOGICZNY
AUTOMATYKA I ROBOTYKA
LABORATORIUM Z FIZYKI
Ćwiczenie nr 12
Temat: Wyznaczanie przerwy energetycznej termistora
I. Wprowadzenie
Zgodnie z teorią pasmową przewodnictwo elektryczne półprzewodników jest wynikiem ruchu elektronów w paśmie przewodnictwa i dziur w paśmie walencyjnym. W temperaturze zera bezwzględnego pasmo walencyjne jest całkowicie wypełnione elektronami, natomiast pasmo przewodnictwa pozbawione jest elektronów w związku z czym przewodnictwo jest minimalne.
Wraz ze wzrostem temperatury następuje przeskakiwanie elektronów
z pasma walencyjnego na pasmo przewodnictwa.
Ilość takich elektronów rośnie wraz ze wzrostem temperatury, a koncentracja elektronów w paśmie przewodnictwa wyraża się wzorem:
gdzie :
n - ilość elektronów w paśmie przewodnictwa
E - energia aktywizacji zależna od rodzaju materiału
k - stała Boltzmanna,
T- temperatura w skali bezwzględnej.
Dla półprzewodnika samoistnego energie aktywacji elektronów i dziur
są jednakowe i równe połowie szerokości przerwy energetycznej.
Dla półprzewodnika domieszkowego sytuacja jest analogiczna tyle,
że E będzie różnicą energii pomiędzy poziomem donorowym a pasmem przewodnictwa.
Zależność tą można sprowadzić do bardziej dla nas przydatnej postaci.:
![]()
gdzie:
R - opór (odwrotność ilości elektronów w paśmie przewodnictwa)
W wyrażeniu tym ( B) jest współczynnikiem kierunkowym prostej charakteryzującej wartość ln(R) względem (1/T).
II. Przebieg ćwiczenia.
W stosowanym układzie pomiarowym miarą gęstości nośników ładunku generowanych termicznie w termistorze jest odwrotność oporu termistora.
Pomiary oporu termistora w zależności od temperatury, wykonujemy za pomocą cyfrowego miernika oporu z dokładnością do ±3 na trzecim miejscu po przecinku, natomiast błąd pomiaru temperatury wynosi 1 K. Należy tu nadmienić, że jest to błąd samego termometru - nie jest brana pod uwagę różnica temperatur pomiędzy termistorem a termometrem oraz czas reagowania termometru.
Pomiary zostały przeprowadzone w zakresie 20 - 60 °C co 5 °C
podczas wzrostu temperatury termistora.
Tabela II.1 Wyniki pomiarów dla dwóch termistorów
Lp. |
Temperatura [C] |
Termistor I Opór [k] |
Termistor II Opór [k] |
1 |
20,0 |
39,0 |
58,0 |
2 |
25,0 |
38,5 |
57,1 |
3 |
30,0 |
34,2 |
50,7 |
4 |
35,0 |
30,2 |
44,9 |
5 |
40,0 |
25,3 |
37,7 |
6 |
45,0 |
21,2 |
31,9 |
7 |
50,0 |
17,8 |
26,9 |
8 |
55,0 |
14,9 |
22,6 |
9 |
60,0 |
12,4 |
18,9 |
Lp. |
Temperatura |
Termistor T1
|
Termistor T2
|
|||
|
T [°C] |
1/T |
Oporność R [Ω]
|
lnR
|
Oporność R [Ω] |
lnR
|
1 2 3 4 5 6 7 8 9 |
20 25 30 35 40 45 50 55 60 |
0,05 0,04 0,03 0,028 0,025 0,022 0,02 0,018 0,016 |
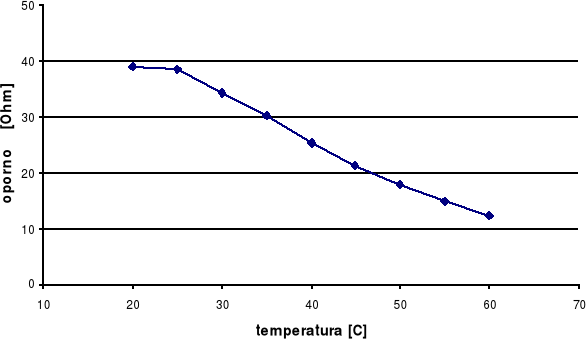
39 38,5 34,2 30,2 25,3 21,2 17,8 14,9 12,4 |
3,663 3,65 3,532 3,407 3,23 3,054 2,879 2,701 2,517 |
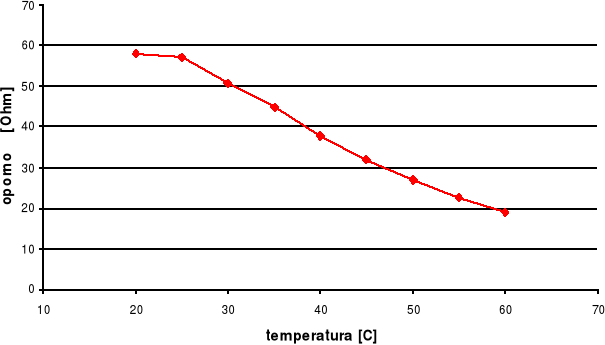
58 57,1 50,7 44,9 37,7 31,9 26,9 22,6 18,9 |
4,06 4,044 3,925 3,804 3,629 3,462 3,292 3,117 2,939 |
Wykres II.1 Zależność oporności od temperatury termistora I
Wykres II.2 Zależność oporności od temperatury termistora II
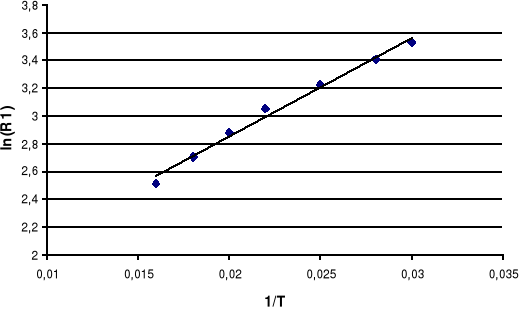
Wykres II.2 Faza wzrostu temperatury termistora I
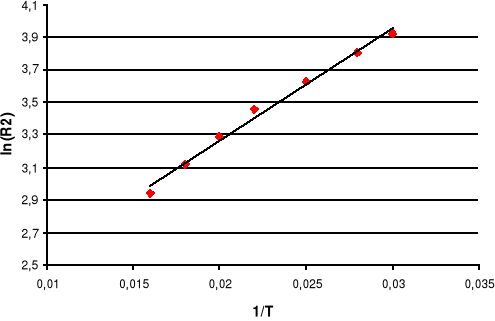
Wykres II.2 Faza wzrostu temperatury termistora II
III. Opracowanie i analiza wyników pomiarów.
Metodą regresji liniowej obliczamy nachylenie charakterystyki lnR=B•1/T, gdzie y=ax+b i B=a. Współczynniki równania y=ax+b obliczamy za wzorów:
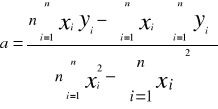
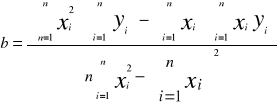
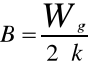
![]()
![]()
a1 = 3,2 ⇒ B1 = 3.2; b1 = (-1.01); współczynnik korelacji r1 = 0.942;
a2 = -0.04 ⇒ B2 = -0.04; b2 = 0.037 współczynnik korelacji r2 = -0.193;
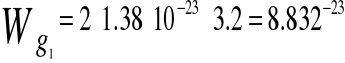
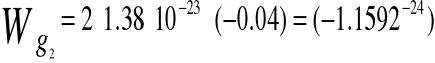
RACHUNEK BŁĘDÓW:
Wszystkie błędy powstałe podczas pomiarów wynikają jedynie z niedokładności przyrządu pomiarowego użytego podczas wykonywania pomiarów. Aby przeprowadzić rachunek błędów należy wziąć pod uwagę klasę dokładności tego przyrządu. Znając ją można obliczyć zarówno błąd względny jak i bezwzględny pomiaru, obydwa zależą bowiem od wartości pomiaru wskazanej przez wyświetlacz miernika. Użyty jako omomierz multimetr cyfrowy Matex-M80 przy zakresie 400 KΩ posiada rozdzielczość 100Ω i klasę dokładności równą 1.2. Zatem:
BŁĄD BEZWZGLĄDNY:
![]()
![]()
BŁĄD WZGLĘDNY:
![]()
![]()
IV. Wnioski i uwagi.
Metoda pomiaru, choć czasochłonna, pozwala wyznaczyć z dużą dokładnością wartość energii aktywacji półprzewodników. Na wartość błędu wpływa tylko dokładność przyrządów pomiarowych, jakie wyznaczają temperaturę i opór. Minimalny błąd odczytu oporu oraz szybki czas reakcji miernika wpływają na wynik w bardzo małym stopniu. Na wykresie nie zaznaczono błędu pomiaru rezystancji, aby nie zmniejszać jego czytelności. Gdyby termometr, zastąpiono przyrządem o większej czułości i dokładności oraz gdyby reagował szybciej na zmiany temperatury można by wyznaczyć E z większą dokładnością. Wpływ na dokładność miałoby także zmniejszenie odległości między termometrem a termistorem.
4
![]()
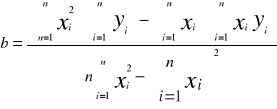
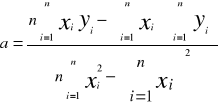
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka