Ćwiczenie 5.

Tytuł: Transformata Z i jej zastosowania.

Tematyka ćwiczenia:

1. Zastosowanie Matlaba do obliczania prostej i odwrotnej transformacji Z. Rozwiązywanie równań różnicowych.

2. Elementy projektowania filtrów cyfrowych.

Zadania do wykonania:

Zadanie 1

Omów krótko polecenia Matlaba umożliwiające znajdowanie symboliczne transformaty Z. Wykorzystując zdobytą w tym temacie wiedzę znajdź transformaty Z następujących funkcji dyskretnych (o parametrach podanych przez prowadzącego zajęcia):

a)

b)

c)

d)

UWAGA: Zamieść odpowiednie kody lub zrzuty ekranowe.

Zadanie 2

Wykorzystując tablicę Z-transformat i rozkład na ułamki proste (odpowiednie polecenie Matlaba) znajdź transformatę odwrotną funkcji:

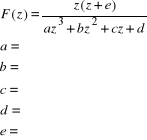
UWAGA: Zamieść odpowiednie kody lub zrzuty ekranowe.

Zadanie 3

Rozwiąż następujące równanie różnicowe:

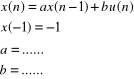
UWAGA: Zamieść odpowiednie kody lub zrzuty ekranowe.

Zadanie 4

Zaprojektuj filtr

1. górnoprzepustowy

2. dolnoprzepustowy

zdolny do odfiltrowania

1. harmonicznej podstawowej

2. składowej harmonicznej o największej częstotliwości z przebiegu podanego przez prowadzącego.

1. Napisz program umożliwiający rysowanie widma amplitudowo-fazowgo zaprojektowanego filtra, jego dyskretną odpowiedź impulsową oraz przebieg badanego sygnału po odfiltrowaniu.

2. Zaproponuj strukturę filtra cyfrowego (wykorzystaj odpowiednie narzędzie pakietu Simulink)

3. Zapoznaj się z możliwościami uniwersalnego programu pakietu Signal Processing SPTool. (wywołanie z Command Line poleceniem >>sptool)

Pomocne funkcje:

1. Projektowanie filtrów w postaci transmitancji (wielomiany w liczniku i mianowniku).

[b,a] = butter(n,Wn,'high') projektuje górnoprzepustowy filtr n-tego rzędu gdzie Wn jest względną częstotliwością odcięcia filtra. Wn=1 odpowiada połowie częstotliwości próbkowania.

[b,a] = butter(n,Wn,'s') projektuje filtr dolnoprzepustowy.

2. Wyznaczanie odpowiedzi częstotliwościowej filtra

freqz(b,a,n,Fs) wyznacza (rysuje) odpowiedź częstotliwościową w zakresie 0 - Fs/2 (częstotliwość Nyquista), n liczba punktów pomiarowych.

3. Wyznaczanie (rysowanie) odpowiedzi impulsowej dyskretnej:

[h,t] = impz(b,a) oblicza odpowiedź impulsową filtra (opisanego wektorami współczynników wielomianów licznika a I mianownika b

[h,t] = impz(b,a,n) oblicza n próbek odpowiedzi (w poprzednim przypadku wartość ta jak I częstotliwość próbkowania dobierane są automatycznie)

4. Filtrowanie zadanego przebiegu

y = filter(b,a,x) filtruje zbiór danych x filtrem opisanym zadaną transmitancją (b,a).

5. Zaprojektowanie wybranej realizacji filtra (podanie struktury, schematu blokowego).

Filter Realization Wizard jest narzędziem do automatycznego projektowania zadanych realizacji filtrów cyfrowych o wybranych architekturach. FRW jest dostępne jako model biblioteki DSP Blockset pakietu Simulink (podkatalog Filter Realizations)

Zadanie 4. (Przykładowe)

Elementy projektowania filtrów cyfrowych

Zadanie do wykonania:

Zaprojektuj filtr

3. górnoprzepustowy

4. dolnoprzepustowy

zdolny do odfiltrowania

3. harmonicznej podstawowej

4. składowej o największej częstotliwości

z przebiegu:

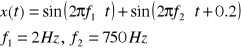
%rząd filtra R

R=1;

%częstotliwość próbkowania fs

fs=1024;

%częstotliwość odcięcia

fc=100;

Wn=fc/(0.5*fs);

[b,a]=butter(R,Wn,'high')

%liczba próbek N

N=128;

freqz(b,a,N,fs);

pause

[y,t] = impz(b,a,11);

stem(t,y);grid;

pause

%filtracja sygnału

t=0:2/1024:1-(2/1024);

x1=sin(2*pi*2.*t);

x2=sin(2*pi*750.*t+0.2);

y=x1+x2;

subplot(2,1,1);plot(t,y);grid;ylabel('x(t)');xlabel('time');

yy=filter(b,a,y);

subplot(2,1,2);plot(t,yy);grid;ylabel('y(t)--> po filtracji');xlabel('time')DODATEK Rozwiązanie

Parametry filtra Butterwortha:

b =

7.594176174499878e-001 -7.594176174499878e-001

a =

1.000000000000000e+000 -5.188352348999757e-001

Odpowiedź częstotliwościowa:

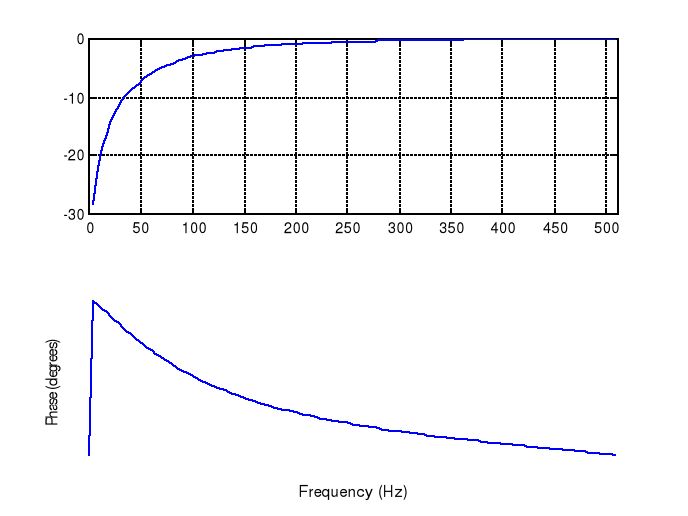
Dyskretna odpowiedź impulsowa:

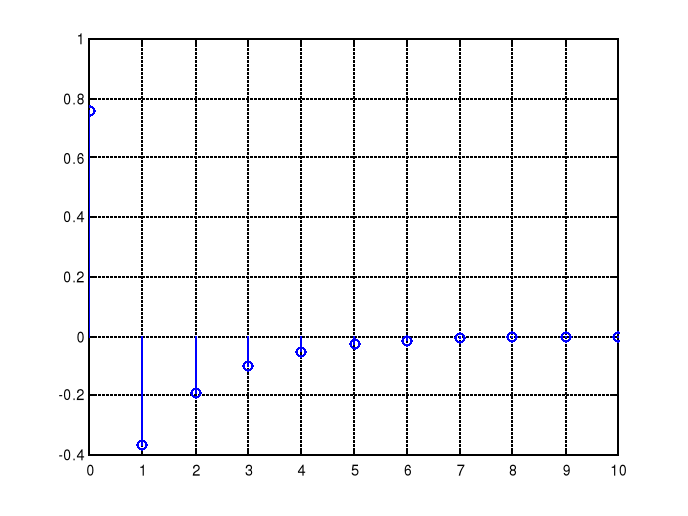
Ilustracja odfiltrowania harmonicznej o niskiej częstotliwości:

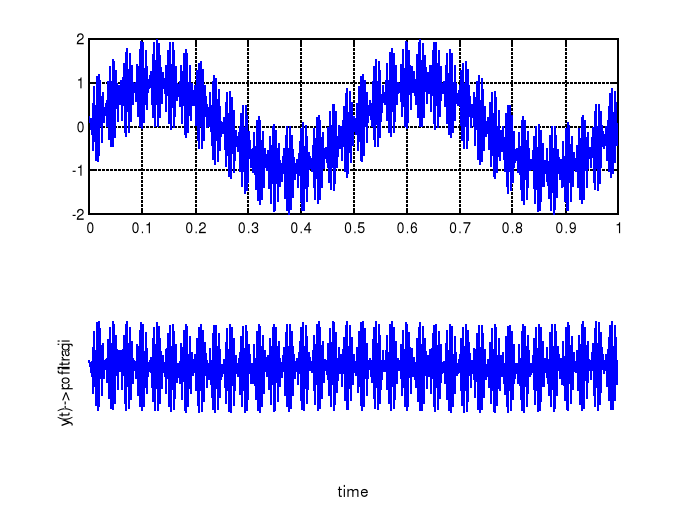
Przykładowa realizacja architektury filtra za pomocą narzędzia FRW:

Przykładowa realizacja

---