MACIERZE

1^o Definicja macierzy.

Funkcję f: (i,k) a_ik taką, że i
M= {1,2,...,m}, k
N= {1,2,...,n} nazywamy macierzą prostokątną wymiaru

mxn o elementach (wyrazach) a_ik = f (i,k), co zapisujemy w postaci

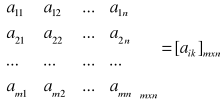
Wynika stąd, że macierz jest tabelą o m-wierszach i n-kolumnach.

Jeżeli a_ik
Z dla (i,k)
M x N, to macierz tę nazywamy macierzą liczbową (zespoloną).

Jeśli a_ik
R, to macierz taką nazywamy rzeczywistą.

2^o Działania na macierzach liczbowych.

I Równość macierzy

[a_ik]_mxn = [b_ik]_mxn <=>  a_ik= b_ik

(i,k)
M x N

II Dodawanie i odejmowanie macierzy

[a_ik ]_mxn
[b_ik ]_mxn = [a_ik
b_ik]_mxn

III Mnożenie macierzy przez liczbę

 [a_ik]_mxn = [ a_ik]_mxn , 


IV Mnożenie macierzy

_{def p}

[a_ij]_mxp ^. [b_jk]_pxn = [c_ik]_mxn , gdzie c_ik = a_ij ^. b_jk

^j=1

Z definicji powyższej wynika, że:

- pierwsza macierz (mnożna) musi posiadać tyle kolumn ile druga (mnożnik) wierszy.

nawet, jeśli istnieje iloczyn A^.B i B^.A.

Przykład 1

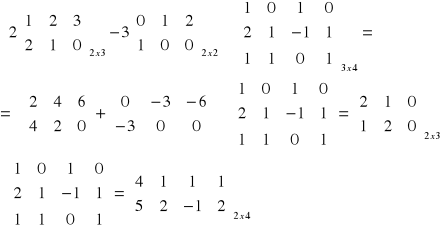
3^o Rodzaje macierzy

Macierz A^T nazywamy transponowaną do macierzy A, jeżeli zamienimy w niej wiersze na kolumny i na odwrót.

Przykład 2

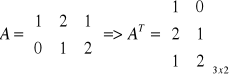
Przykład 3

Oblicz:

Dla

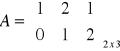
mamy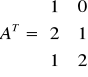

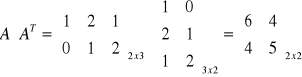
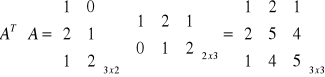
Macierz [A_ik]_mxn złożoną z samych zer nazywamy macierzą zerową

i

Macierz, w której m=n, nazywamy macierzą kwadratową.

4^o Macierze kwadratowe.

Macierz kwadratową A = [a_ik]_nxn nazywamy osobliwa, jeżeli

.

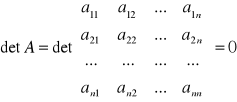
W przeciwnym wypadku macierz liczbową nazywamy nieosobliwą.

A=[a_ik] nazywamy diagonalną, jeżeli a_ik = a_ik δ_ik ,

gdzie

δ_ik = { 0 , i = k} i {1, i=k}

jest deltą Kroneckera, a det oznacza determinantę (wyznacznik) macierzy.

Zauważmy, że

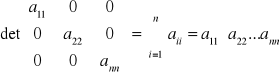
Jeżeli a_ii w macierzy diagonalnej

,

to otrzymamy macierz jednostkową

i det I=1.

Gdy w macierzy diagonalnej a_ii = 0 dla

i=1,2,...,n

= 0_nxn det 0_nxn=0

5^o Rząd macierzy

Rzędem r macierzy [a_ik]_mxn nazywamy najwyższy stopień wyznacznika tej macierzy
0 , przy czym r(0_nxn ) = 0.

Wynika stąd, że

r [a_ik]_mxn
min {m,n}.

Przykład 1 I sposób (z definicji)

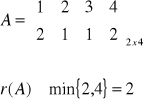
Ponieważ

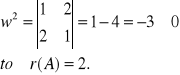
Przykład 2 II sposób (metoda Laplace`a)

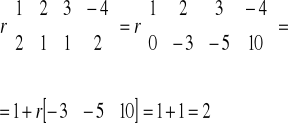
Przykład 3 I sposób( z definicji)

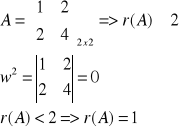
II sposób(Laplace`a)

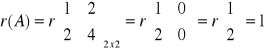
6^o Metoda przekształceń elementarnych macierzy i

macierze równoważne.

Przekształceniami elementarnymi macierzy nazywamy

(i) zamianę wierszy (kolumn) ;

(ii) pomnożenie wiersza (kolumny) przez liczbę
0 ;

(iii) pomnożenie wybranego wiersza (kolumny) przez pewną liczbę i dodanie do innego wiersza (kolumny)

Macierze nazywamy równoważnymi, jeżeli jedna powstaje z drugiej przez zastosowanie działań elementarnych .

Stąd

A~B <=> r (A) = r (B)

(~)- równoważne

Przykład 4

Oblicz rząd macierzy

7^o Macierz odwrotna

Macierz odwrotna A^-1 do macierzy kwadratowej nie-osobliwej A nazywamy taką macierz, że

A^-1A= A A^-1=I

Można dowieść, że

A^-1 =
[A_ik]^T,

gdzie [A_ik]^T jest transponowaną macierzą dopełnień algebraicznych.

Przykład 5.

Znajdź macierz odwrotną do macierzy

A=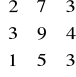

i dokonaj sprawdzenia.

Zauważmy, że

,

to znaczy, że macierz A jest nieosobliwa czyli istnieje

^Ponieważ

,

to

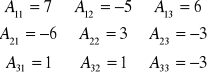
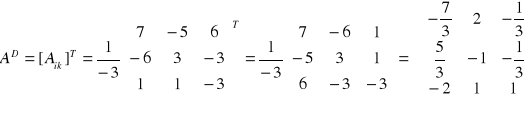
Sprawdzenie

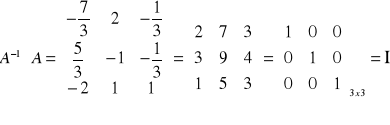
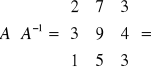
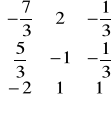
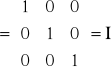
Uwaga

Stosując metodę przekształceń elementarnych do dwóch macierzy działania dotyczą tylko wierszy

Przykład 6

Stosując powyższy algorytm oblicz A^-1 dla

Sprawdzenie

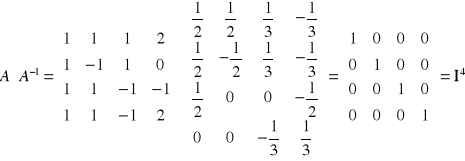
A^-1.A=
.

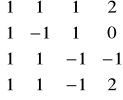
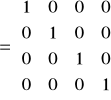
- 77 -

---