Miernictwo	Ocena:
semestr: zimowy	Cyfrowa analiza widmowa sygnałów okresowych
Wydział Elektroniki

1. Cel ćwiczenia.

Poznanie zasad pomiaru właściwości elektrycznych sygnałów okresowych w dziedzinie częstotliwości. Do wyznaczenia widma sygnału wykorzystuje się metodę obliczeniową, opisywaną w podręcznikach jako szybka transformata Fouriera (FFT). W ćwiczeniu szczególną uwagę zwrócono na czynniki, które powodują istotne błędy w odtworzeniu widma badanego sygnału.

2. Spis przyrządów.

- komputer klasy PC, program „Widmo”

3. Pomiary.

3.1 Zapoznanie się z obsługą programu komputerowego

Po uruchomieniu programu WIDMO zapoznaliśmy się z obsługą programu na podstawie instrukcji.

Następnie ustawiliśmy dla trybu symulacji parametry

• częstotliwość sygnału:
  

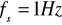
• częstotliwość próbkowania:
  

• 
  

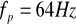
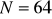
• rozdzielczość przetwornika:
  

wyznaczyliśmy zadane wartości kolejno dla różnych kształtów sygnału.

	Sinusoidalny	Trójkątny	Prostokątny
nh	1 (1)	8	8
	1	1	1

- rozdzielczość widma

n_h - liczba prążków

Obliczamy teoretyczne wartości amplitudy korzystając ze wzorów (a=5V) dla

• kształtu sinusoidalnego:
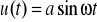
  i że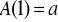
  

• kształtu trójkątnego:
  

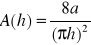
• kształtu prostokątnego:
  

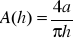
Błąd ΔA liczymy ΔA=|A-A_t|

Sygnał sinusoidalny
h	A	At	ΔA
1	5,000	5,000	0,000

Sygnał trójkątny					Sygnał prostokątny
h	A	At	ΔA		h	A	At	ΔA
1	4,056	4,057	0,001		1	6,368	6,369	0,001
3	0,453	0,451	0,002		3	2,129	2,123	0,006
5	0,165	0,162	0,003		5	1,286	1,274	0,012
7	0,086	0,083	0,003		7	0,927	0,910	0,017
9	0,053	0,050	0,003		9	0,730	0,708	0,022
11	0,036	0,035	0,002		11	0,607	0,579	0,028
13	0,027	0,024	0,003		13	0,524	0,490	0,034
15	0,020	0,018	0,002		15	0,465	0,425	0,040

h - numer prążka

A - amplituda zmierzona

A_t - amplituda teoretyczna

ΔA - błąd

3.2 Badanie zjawiska nakładania się widma w trybie symulacji pomiaru.

Dla sygnału trójkątnego spisaliśmy wartości amplitudy prążków z zakresu 1-15. W poniższej tabelce przedstawiamy wartości zmierzonej amplitudy (A) i odpowiadającej jej amplitudzie teoretycznej (A_t). A_t liczymy ze wzorów przedstawionych w punkcie 3.1. Błąd ΔA liczymy ΔA=|A-A_t|. Zgodnie z poleceniem stosunek f_p/f_s = N został tak dobrany by

• N = 32 => f_s=1 f_p=32

• N = 64 => f_s=1 f_p=64

• N = 128 => f_s=1 f_p=128

• N = 256 => f_s=1 f_p=256

Tabela wartości zmierzonych i wartości teoretycznej dla sygnału prostokątnego:

	N=32	N=64	N=128
h	A	A	A	At
1	4,065	4,056	4,053	4,057
3	0,463	0,453	0,451	0,451
5	0,175	0,165	0,162	0,162
7	0,097	0,086	0,083	0,083
9	0,065	0,053	0,050	0,050
11	0,050	0,036	0,034	0,035
13	0,042	0,027	0,024	0,024
15	0,035	0,020	0,018	0,018

Tabela błędów:

	N=32	N=64	N=128
h	ΔA	ΔA	ΔA
1	0,008	0,001	0,004
3	0,013	0,002	0,002
5	0,013	0,003	0,001
7	0,014	0,003	0,000
9	0,015	0,003	0,000
11	0,015	0,001	0,001
13	0,017	0,003	0,000
15	0,017	0,002	0,000

Przebieg części ćwiczenia dla sygnału prostokątnego jest podobny jak dla sygnału trójkątnego. Spisane zostały wszystkie możliwe amplitudy prążków jednak tutaj w analizie uwzględnimy tylko cztery wspólne dla wszystkich przypadków. Wartość teoretyczną i błędy liczymy w identyczny sposób.

Tabela wartości zmierzonych i wartości teoretycznej dla sygnału prostokątnego:

	N=32	N=64	N=128	N=256
h	A	A	A	A	At
1	6,376	6,368	6,366	6,366	6,366
3	2,153	2,129	2,123	2,122	2,123
5	1,325	1,286	1,276	1,276	1,274
7	0,985	0,927	0,913	0,910	0,910
9	0,808	0,730	0,713	0,708	0,708
11	0,708	0,607	0,585	0,580	0,579
13	0,607	0,524	0,498	0,491	0,490
15	0,514	0,465	0,434	0,426	0,425

Tabela błędów:

	N=32	N=64	N=128	N=256
h	ΔA	ΔA	ΔA	ΔA
1	0,010	0,002	0,000	0,000
3	0,030	0,006	0,000	0,001
5	0,051	0,012	0,002	0,002
7	0,075	0,017	0,003	0,000
9	0,100	0,022	0,005	0,000
11	0,129	0,028	0,006	0,001
13	0,117	0,034	0,008	0,001
15	0,089	0,04	0,009	0,001

3.3 Badanie zjawiska przenikania widma.

Jako pierwszą czynność w tym punkcie sprawdziliśmy wpływ momentu rozpoczęcia zbierania N = 64 próbek sygnału sinusoidalnego na wynik pomiaru.f_p=256, f_s=4, rozdzielczość przetwornika = ∞. Przesuwając okno czasowe wzdłuż badanego sygnału nie stwierdziliśmy żadnego wpływu momentu, od którego rozpoczynamy proces zbierania N próbek na wynik pomiaru.

Następnie zbadaliśmy wpływ niewielkich zmian f_p na wynik pomiarów widma.

Z programu odczytaliśmy wartości A w decybelach. By otrzymać wartości w woltach skorzystaliśmy ze wzoru

f_p=255 Hz

f_s=4 Hz

skala logarytmiczna

h	An [dB]	An [V]
1	0	5
2	-45,58	0,0263
3	-50,58	0,0147
4	-53,52	0,0105
5	-55,63	0,0082
6	-57,29	0,0068
7	-58,65	0,0058

Jak widać nawet minimalna desynchronizacja f_p i f_s prowadzi do powstawania zjawiska przenikania widma - widmo częstotliwościowe jest „rozmywane”. W tym przypadku stwierdziliśmy również wpływ momentu rozpoczęcia zbierania N próbek na wynik pomiaru.

3.4 Określenie wpływu rozdzielczości przetwornika A/C na widmo częstotliwościowe.

Wykonaliśmy symulację pomiarów widma sygnału sinusoidalnego przy warunkach (f_p/f_s)= N = 64 oraz z ustawieniem przetwornika
. Dla niego otrzymujemy jeden prążek o wartości 5V.

Następnie zmienialiśmy rozdzielczość przetwornika i obserwowaliśmy widmo sygnału.

4. Wnioski

W punkcie 3.1 zapoznawaliśmy się z obsługą programu WIDMO. Wykonywaliśmy symulację widma trzech sygnałów: trójkątnego, prostokątnego i sinusoidalnego. Dla przebiegu sinusoidalnego wartość amplitudy odczytana z programu była taka sama, jak wartość teoretyczna, dla pozostałych dwóch sygnałów wartości różniły się. Wynika to z samej natury określania takich sygnałów przez przebiegi sinusoidalne za pomocą szeregów Fouriera.

W następnym punkcie badaliśmy zjawiska nakładania się widma w trybie symulacji pomiaru. Na podstawie obserwacji, stwierdzam, że zwiększając stosunek f_p/f_s wartości amplitud kolejnych prążków dla badanych sygnałów "zbliżały się" do wartości teoretycznych.

W punkcie 3.3 badaliśmy zjawisko przenikania widma. Wykonaliśmy symulacje pomiarów widma sygnału sinusoidalnego dla ustawień: (f_P/f_S)=N=64, przetwornik
. Mieliśmy stwierdzić czy na wyniki pomiarów wpływa moment od którego zaczynamy proces zbierania próbek. Na podstawie przeprowadzone obserwacji, mogę stwierdzić, że wybór momentu, od którego będziemy zbierać próbki nie ma żadnego wpływu na wyniki pomiarów.

Następnie zmniejszyliśmy minimalnie częstotliwość próbkowania dla sygnału sinusoidalnego, dla którego teoretycznie w próbkowaniu w jednym okresie pojawia się jeden prążek. Tę zmianę spowodowało zróżnicowanie okresu pomiaru, który już nie był wielokrotnością jednego pełnego okresu. Spowodowało to pojawienie się nowych prążków które wyraźnie było widać w skali logarytmicznej.

Na koniec badaliśmy wpływ rozdzielczości przetwornika A/C na widmo. Okazuje się, że im przetwornik ma mniejszą liczbę bitów (moc obliczeniową) tym pojawiało się dla sygnału sinusoidalnego coraz więcej prążków. Mniejsza liczba bitów niekorzystnie wpływa na pomiary widma.

W cyfrowej analizie widmowej sygnałów okresowych by uniknąć błędów trzeba przyjmować odpowiednio dużą częstotliwość próbkowania ponieważ przy mniejszej występuje nakładanie się widma (zgodnie z twierdzeniem Shannona-Kotielnikowa f_p powinno być dwa razy większe od częstotliwości granicznej). ). Czas rejestracji musi być wielokrotnością sygnału bo w innym wypadku mamy do czynienia z przenikaniem widma. Im większa rozdzielczość przetwornika tym lepiej.

---