Analiza współzależności

I. Współzależność cech ilościowych

Współczynnik korelacji liniowej Pearsona

=

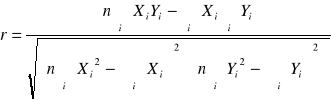
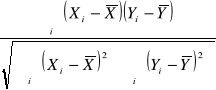
Z kalkulatora

Mode, Stat, a+bx, wprowadzany dane w kolumnach X,Y (=) , zapamiętujemy dane AC, odczyt danych Shift, Stat, Reg r

Mode, Reg, Lin, wprowadzamy dane parami X,Y zapamiętujemy każdą parę M+, odczyt danych Shift, S-Var, > > r

II. Współzależność cech porządkowych

Współczynnik korelacji liniowej rang Spearmana:

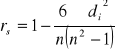
gdzie:

Z kalkulatora

Mode, Stat, a+bx, wprowadzany dane w kolumnach r1,r2 (=) , zapamiętujemy dane AC, odczyt danych Shift, Stat, Reg r

Mode, Reg, Lin, wprowadzamy dane parami r1,r2 zapamiętujemy każdą parę M+, odczyt danych Shift, S-Var, > > r

III. Współzależność cech jakościowych

Współczynnik zbieżności T-Czuprowa:

,

, (
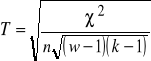
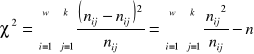
), n to całkowita liczba par obserwacji,
to liczebności empiryczne (z próby),
to liczebności teoretyczne, , w to liczba wierszy, k to liczba kolumn w tablicy kontyngencji

Współczynnik asocjacji
-Yula:

=
,

=
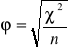
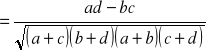
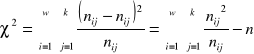
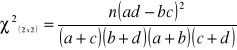
, gdy:

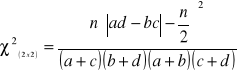
, gdy:
(lub
) tzw. poprawkę Yates'a

Regresja liniowa

„a” to wyraz wolny (nie interpretujemy)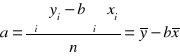

„b” to współczynnik regresji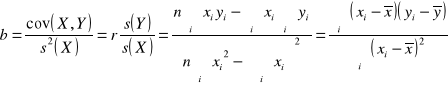

Int. Wzrost X o 1 jednostkę powoduje wzrost (b>0)/spadek(b<0) wartości Y średnio o ………………..

Miary dopasowania funkcji regresji liniowej do danych

:
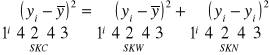
SKC=SKW+SKN

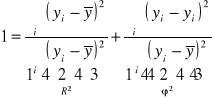
1. Współczynnik zbieżności (indeterminancji)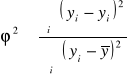
,

Int. φ ² to udział zmienności ………………… regresją w całkowitej zmienności Y (w ilu % Y ………….. od X).

Int. w φ² 100% zmienność Y ………………… wyjaśniona (regresją liniową) zmiennością X

2. Współczynnik determinacji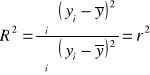
,
,
(regresja liniowa)

Int. R ² to udział zmienności ……………………….regresją w całkowitej zmienności Y (w ilu % Y ……….od X).

Int. R² 100% zmienność Y ………………………. wyjaśniona (regresją liniową) zmiennością X .

3. Odchylenie standardowe reszt (średni błąd szacunku)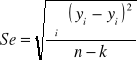
=

Gdzie:
(reszta), k to liczba parametrów funkcji regresji (k=2).

Int. Rzeczywiste wartości zmiennej Y różnią się od oszacowanych na podstawie funkcji regresji liniowej średnio (+/-) ………………..

4. Współczynnik zmienności przypadkowej (względny średni błąd szacunku)

Int. Rzeczywiste wartości zmiennej Y różnią się od przeciętnych oszacowanych na podstawie funkcji regresji liniowej średnio (+/-) o ……………………….

Wniosek: natężenie wahań przypadkowych (losowych) jest ...........(małe/ umiarkowane/ średnie/ duże).

Regresja krzywoliniowa

I. Regresja funkcją hiperboliczną

„b” nie interpretujemy,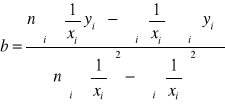

„a” to poziom nasycenia (asymptota funkcji),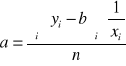

Int. Jeżeli b>0, to Y maleje do nieprzekraczalnego-minimalnego poziomu a.

Int. Jeżeli b<0, to Y rośnie do nieprzekraczalnego-maksymalnego poziomu a.

II. Regresja funkcją potęgową
=>

„a” to wyraz wolny (nie interpretujemy)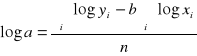

„b” to współczynnik elastyczności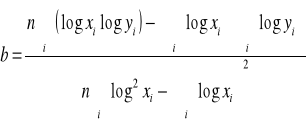

Int. Wzrost X o 1% powoduje wzrost (b>0)/spadek (b<0) wartości Y średnio o b%.

III. Regresja funkcją wykładniczą
=>

„a” to wyraz wolny (nie interpretujemy)

„b” to stopa przyrostu (średni przyrost względny).

Int. Wzrost X o jednostkę powoduje wzrost (b>1)/spadek (0<b<1) wartości Y średnio o (b-1)100%.

=>

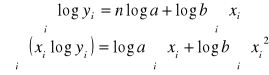
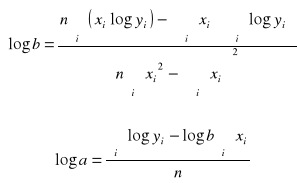
Wzory analiza współzależności Strona 3

---