Podstawowym narzędziem ekonometrii jest model. Jest to równanie lub układ równań, które przedstawiają zależność pewnych zmiennych ekonomicznych od innych zmiennych.
![]()
W badaniach najczęściej wykorzystuje się model w postaci liniowej:
![]()
,
![]()
(X0t = 1 tzw. zmienna ślepa)
Yt - zmienna objaśniana (endogeniczna), Xit - zmienne objaśniające (egzogeniczne), ![]()
- składnik losowy (jest również zmienną losową), ![]()
- parametry strukturalne.
Przyczyny występowania składnika losowego w równaniu regresji:
1. Losowa natura zjawisk i procesów gospodarczych.
2. W równaniu nie uwzględniamy wszystkich przyczyn powodujących kształtowanie się zmiennej objaśnianej.
3. Przyjęta analityczna postać funkcji regresji nie odpowiada dokładnie rzeczywistej formie zależności między badanymi zmiennymi.
4. Niedokładność w obserwacji i pomiarze zjawisk i procesów.
5. Zaokrąglenia w obliczeniach.
Wprowadzenie do modelu składnika losowego nadaje zależności charakter stochastyczny. Bez składnika losowego model jest deterministyczny.
Parametry struktury stochastycznej to parametry rozkładu składnika losowego (własności składnika losowego):
![]()
wartość oczekiwana równa zeru
![]()
stała i skończona wariancja
Macierz wariancji - kowariancji składników losowych dana jest wzorem:
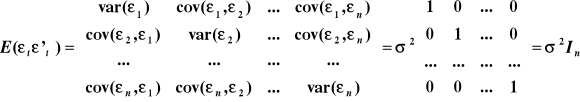
gdzie In jest to macierz jednostkowa,
![]()
stała wariancja
![]()
nie występuje autokorelacja składnika losowego.
Dodatkowo zakłada się, że rozkład składnika losowego jest normalny.
Klasyfikacja modeli ekonometrycznych
W zależności od przyjętego kryterium możemy wyróżnić różne rodzaje modeli:
1) ze względu na liczbę równań w modelu:
- jednorównaniowe
- wielorównaniowe
2) ze względu na postać analityczną:
- liniowe
![]()
- nieliniowe (najczęściej spotykane w badaniach empirycznych):
Postać potęgowa (jeżeli wiadomo, że elastyczność zmiennej objaśnianej ![]()
względem zmiennych objaśniających ![]()
jest stała):
![]()
![]()
- oznacza elastyczność zmiennej ![]()
względem zmiennej ![]()
.
Przykładem funkcji potęgowej jest funkcja produkcji typu Cobba - Douglasa:
![]()
gdzie: Y - wartość produkcji, X1 - kapitał, X2 - zatrudnienie
![]()
- informuje w przybliżeniu o ile procent zmieni się produkcja, jeżeli kapitał zmieni się o 1%,
![]()
- informuje w przybliżeniu o ile procent zmieni się produkcja, jeżeli wielkość zatrudnienia zmieni się o 1%,
Model w postaci potęgowej sprowadza się do postaci liniowej poprzez logarytmowanie obu stron równania.
Innym przykładem modeli nieliniowych są krzywe Törnquista (patrz J.W. Wiśniewski, Z. Zieliński, Elementy Ekonometrii)
Postać logarytmiczna (jeżeli jednostkowemu przyrostowi zmiennej objaśniającej towarzyszą coraz mniejsze przyrosty zmiennej objaśnianej):
![]()
![]()
np. zależność indywidualnej wydajności pracy robotników (![]()
) od stażu pracy w danym zawodzie (![]()
).
Postać wykładnicza (jeżeli jednostkowemu przyrostowi zmiennej objaśniającej odpowiadają coraz większe przyrosty zmiennej objaśnianej):
![]()
np. zależność kosztów całkowitych produkcji (![]()
) od wielkości produkcji (![]()
).
Postać hiperboliczna:
![]()
np. zależność między inflacją a bezrobociem - Krzywa Philipsa
Postać wielomianowa:
![]()
![]()
(ze zmienną czasową t, z trendem)
Wśród modeli nieliniowych można wyróżnić modele nieliniowe względem zmiennych objaśniających i jednocześnie liniowe względem parametrów strukturalnych, np. postać logarytmiczna i hiperboliczna oraz modele nieliniowe zarówno względem zmiennych objaśniających, jak i względem parametrów strukturalnych, np. postać potęgowa.
3) ze względu na kryterium czasu:
-dynamiczne (opisują procesy stochastyczne, realizacje dotyczą okresu czasu, np. kolejne dni, miesiące, lata)
-statyczne (opisują zmienne losowe, realizacje dotyczą określonego momentu)
-dynamiczno-statyczne(opisują pola losowe)
4) ze względu na walory poznawcze:
- przyczynowo - skutkowe (zmienna objaśniana jest skutkiem a zmienne objaśniające przyczynami)
- symptomatyczne (zmienne objaśniające są silnie skorelowane ze zmienną objaśnianą, ale nie są jej przyczynami)
- tendencji rozwojowej (ze zmienną czasową t, czyli modele z trendem)
- autoregresyjne (w roli zmiennych objaśniających występuje opóźniona w czasie zmienna objaśniana)
![]()
5) ze względu na charakter zależności:
- stochastyczne
- deterministyczne
6) ze względu na przedmiot badań:
modele opisujące strukturę: zdarzeń, zmiennych losowych, procesów stochastycznych, pól losowych,
modele opisujące zależności między zdarzeniami, zmiennymi losowymi, procesami stochastycznymi, polami losowymi.
Etapy budowy modelu ekonometrycznego:
1. Specyfikacja
2. Identyfikacja
3. Zebranie materiału statystycznego
4. Estymacja parametrów
5. Weryfikacja modelu
6. Zastosowanie modelu - praktyczne wykorzystanie
ad 1. Specyfikacja
Należy określić między innymi cel i zakres badania oraz wybrać metodę. Wyróżniamy:
a) specyfikację zmiennych
b) specyfikację równań (wybór analitycznej postaci modelu)
Specyfikacja zmiennych: określamy zmienną objaśnianą i zmienne objaśniające. Najpierw wybieramy potencjalne zmienne objaśniające. Wyboru dokonujemy na podstawie teorii ekonomicznej, wiedzy ekspertów, doświadczenia.
Redukcja zbioru zmiennych potencjalnych
- zmienne objaśniające powinny być silnie skorelowane ze zmienną objaśnianą
- zmienne objaśniające powinny być słabo skorelowane między sobą.
Metody redukcji zbioru zmiennych potencjalnych:
- metoda pojemności integralnych Hellwiga (wskaźników pojemności informacyjnej)
- metoda Bartosiewiczowej (metoda analizy grafów)
- metoda selekcji a posteriori.
ad 2. Identyfikacja - dotyczy modeli wielorównaniowych
ad 4. Estymacja. Szacujemy parametry strukturalne i parametry struktury stochastycznej.
Estymator jest to pewna funkcja określona na próbie, która służy do oszacowania nieznanej wartości parametru w populacji generalnej.
Własności estymatorów:
1. nieobciążoność: ![]()
gdzie: ![]()
oznacza parametr, a Tn - estymator
Odchylenia wartości estymatora od wartości parametru nie mają tendencyjnego charakteru (nie ma błędu systematycznego).
2. zgodność
![]()
dla dowolnego ![]()
Wraz ze wzrostem liczby obserwacji wzrasta dokładność szacunku.
3. efektywność
Estymator jest najefektywniejszy, jeżeli ma najmniejszą wariancję.
4. dostateczność
Estymator jest dostateczny, jeżeli zawiera wszystkie informacje, jakie występują w próbie na temat parametru i żaden inny estymator nie może dać dodatkowych informacji o szacowanym parametrze.
Metody estymacji: KMNK (klasyczna metoda najmniejszych kwadratów), UMNK (uogólniona metoda najmniejszych kwadratów), PMNK (pośrednia metoda najmniejszych kwadratów), 2MNK (podwójna metoda najmniejszych kwadratów), metoda największej wiarygodności.
KMNK polega na znalezieniu takich ocen parametrów strukturalnych, przy których suma kwadratów odchyleń rzeczywiście zaobserwowanych wartości zmiennej objaśnianej od wartości teoretycznych wyznaczonych z modelu jest najmniejsza.
Model klasycznej regresji liniowej:
![]()
![]()
- wektor obserwacji na zmiennej endogenicznej, ![]()
- macierz obserwacji na zmiennych egzogenicznych, ![]()
- wektor parametrów strukturalnych, ![]()
- wektor składników losowych.
założenia:
X- nielosowe,
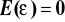
,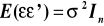
.
Parametry ![]()
szacujemy MNK (metodą najmniejszych kwadratów).
Wektor ocen parametrów strukturalnych ![]()
dany jest wzorem:
![]()
Parametry struktury stochastycznej: błędy średnie estymatorów i wariancja resztowa.
Macierz wariancji-kowariancji estymatorów parametrów ![]()
:
![]()
Na przekątnej tej macierzy znajdują się wariancje estymatorów:
![]()
![]()
- diagonalny element macierzy ![]()
pierwiastek z wariancji estymatora to błąd średni estymatora (błąd szacunku parametru):
![]()
Nieobciążonym estymatorem wariancji składnika losowego ![]()
jest wariancja składnika resztowego ![]()
(wariancja resztowa):
![]()
,
gdzie ![]()
, ![]()
, k - liczba zmiennych objaśniających (1 dla wyrazu wolnego).
ad 5. Weryfikacja modelu. Wyróżniamy:
- weryfikację statystyczną
- weryfikację ekonomiczną
Weryfikacja statystyczna obejmuje:
a) badanie istotności parametrów strukturalnych. Sprawdzamy, czy zmienne objaśniające uwzględnione w modelu istotnie wpływają na zmienną objaśnianą.
b) badanie dopasowania modelu do danych empirycznych
c) badanie rozkładu reszt (sprawdzanie, czy spełnione są przyjęte przy estymacji założenia):
sprawdzamy czy wariancja bezwarunkowa składnika losowego jest stała - np. test F,
czy wariancja warunkowa jest stała - test Engle'a (LM) - tylko dla szeregów czasowych,
czy reszty mają charakter losowy - test serii,
czy reszty mają rozkład normalny - np. test Jarque-Bera, test Shapiro-Wilka, test zgodności
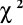
, test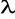
-Kołmogorowa,badanie autokorelacji składnika losowego - np. test Durbina-Watsona, test Ljunga - Boxa (badanie autokorelacji tylko dla szeregów czasowych).
1
3
Wyszukiwarka