1. parcie gruntu - ciśnienie działające na ścianę oporową skierowane jest w kierunku od gruntu,
2.odpór gruntu - ciśnienie działające na ścianę oporową skierowane jest w kierunku do gruntu,
3. założenia metody Coulomba (parcie gruntu):
- grunt za ścianą nie ma spójności, jest jednorodny i izotropowy,
- ściana muru oporowego jest pionowa, a naziom poziomy,
- między ścianą a gruntem nie występuje tarcie, dlatego kierunek parcia Ea jest poziomy,
- poślizg gruntu następuje wzdłuż płaszczyzny odłamu nachylonej pod pewnym kątem α do poziomu, przechodzącej przez dolną tylną krawędź muru oporowego,
- klin odłamu jest ciałem sztywnym i znajduje się w stanie równowagi granicznej,
- nachylenie płaszczyzny odłamu α określa się z warunku ekstremum parcia gruntu.
Ea = (![]()
γn + pH)Ka
Ea - parcie czynne,
γn - ciężar objętościowy gruntu,
p - siła obciążenia naziomu,
Ka - współczynnik parcia czynnego.
4. założenia metody Renduliča (parcie gruntu):
- powierzchnia poślizgu jest w przekroju spiralą logarytmiczną,
- kąt pomiędzy kierunkiem promienia a normalną do powierzchni poślizgu równa się kątowi tarcia wewnętrznego,
- c ≠ 0, φ ≠ 0,
- eliminuje się ciśnienie występujące pod kątem φ do normalnych do linii poślizgu,
- niewiadome: siła E i ciężar klina gruntu,
- równanie spirali : r = r0 exp(-α tgφ),
- dla określenia E zakładamy położenie spirali, Emax i Emin określa się metodą prób i błędów.
5. najważniejsze zastosowania koła zniszczeń Mohra:
- określenie linii zniszczeń Coulomba-Mohra,
- określenie c,
- określenie φ.
6. założenia teorii Boussinesqa:
- podłoże gruntowe stanowi półprzestrzeń ograniczoną od góry płaszczyzną a nieograniczoną w innych kierunach,
- ośrodek gruntowy jest izotropowy i nieważki (γ = 0),
- przyjmuje się zależność liniową między naprężeniami a odkształceniami - obowiązuje prawo Hooke'a,
- obowiązuje zasada superpozycji,
- sposób przyłożenia obciążenia, zgodnie z zasadą Saint-Venanta wpływa na rozkład naprężeń tylko w bliskim sąsiedztwie miejsca przyłożenia obciążenia.
- naprężenia poniżej płaszczyzny układają się w ten sposób, że każda wydzielona myślowo półkula ze środkiem w punkcie O obniży się na całej powierzchni o jednakowy odcinek ΔZ,
- ![]()
, naprężenia w dowolnym punkcie półkuli pod kątem β
- ![]()
, naprężenia w dowolnym punkcie półkuli pionowe.
7. zdefiniować podłoże budowli.
- podłoże budowli to strefa pod punktem przyłożenia obciążenia do głębokości na której naprężenia dodatkowe od obiektu σzd równa się 0,3 naprężeń pierwotnych efektywnych σzγ.
8. wymienić rodzaje wytrzymałości gruntu; przedstawić zasadę badania w aparacie skrzynkowym.
- wytrzymałość gruntu - zdolność gruntu do przeciwstawiania się zniszczeniu lub nieograniczonym odkształceniom,
- wytrzymałość na ściskanie,
- wytrzymałość na rozciąganie,
ściskanie: jednoosiowe (bez odkształceń bocznych; z odkształceniami bocznymi)
rozciąganie: rozciąganie klasyczne, metoda brazylijska, zginanie,
ścinanie: aparat skrzynkowy, aparat trójosiowy, ring shear, vane test.
aparat ring shear - oznaczanie wytrzymałości rezydualnej
Schemat skrzynki aparatu bezpośredniego
ścinania
1 - skrzynka dolna,
2 - skrzynka górna,
3 - pokrywa,
4 - filtry o ząbkowanej powierzchni,
5 - wymuszona płaszczyzna ścięcia.
Aparat bezpośredniego ścinania (aparat skrzynkowy) składa się z metalowej skrzynki podzielonej poziomo na dwie części, które mogą przesuwać się względem siebie. Próbkę gruntu z zazębianymi płytkami oporowymi umieszcza się w skrzynce, a następnie obciąża siłą pionową Q i ścina wskutek przesuwu względem siebie części skrzynki pod wpływem poziomej siły T. Maksymalna siła Tmax, przy której nastąpiło ścięcie, odniesiona do pola przekroju płaszczyzny ścięcia próbki, jest naprężeniem ścinającym τ = Tmax / A równym wytrzymałości a ścinanie τf (τf = τf).
Wady aparatu skrzynkowego:
- niemożność pomiaru ciśnienia wody w porach,
- nierównomierny rozkład naprężeń stycznych i normalnych w wymuszonej powierzchni ścięcia,
- jednoosiowy stan odkształcenia próbki, który nie odpowiada warunkom rzeczywistym,
- miejscowe zaklinowanie ziarn (przy krawędziach) w związku z wymuszoną powierzchnią ścinania, co zwiększa mierzony opór τf,
- niemożność jednoznacznego opisu stanu naprężeń w próbce.
9. konsolidacja wtórna, konsolidacja pierwotna, współczynnik konsolidacji, wskaźnik konsolidacji.
- konsolidacja - odkształcenie próbki spowodowane zmianami obciążenia, zachodzące na skutek: usuwania i zagęszczania powietrza i wód porowych, przemieszczania ziarn mineralnych,
- konsolidacja pierwotna - początkowe odkształcenie próbki spowodowane odpływem wody,
- konsolidacja wtórna - odkształcenie próbki spowodowane przemieszczaniem cząstek mineralnych,
- współczynnik konsolidacji zależy od przepuszczalności i ściśliwości, określa tempo konsolidacji gruntu,
10. wytłumaczyć na rysunku naprężeniowy warunek równowagi granicznej łącznie z przedstawieniem co się dzieje z powierzchnią terenu obok budowli.
I faza:
- przyrost osiadań fundamentu i terenu wprost proporcjonalny do przyrostu obciążenia gruntu,
- fundament osiada tylko wskutek ściśliwości gruntu,
- q < qprop,
II faza:
- zwiększenie przyrostu osiadań fundamentu i podnoszenie się terenu obok fundamentu,
- coraz większy wpływ obszarów uplastycznienia gruntu pod krawędziami fundamentu,
- qprop < q < qf,
III faza:
- po osiągnięciu qf fundament zagłębia się bez zwiększania obciążeń, przy jednoczesnym wypieraniu gruntu i przechylaniu się fundamentu,
- osiadanie i przechył fundamentu występują prawie wyłącznie wskutek wypierania gruntu spod fundamentu
- q > qf.
11. przedstawić warunki równowagi zbocza zbudowanego z gruntu sypkiego nawodnionego.
![]()
W - efektywny ciężar elementu [kN]
β - kąt nachylenia zbocza,
φ - kąt tarcia wewnętrznego.
wysokość skarpy nie gra roli.
12. stateczność zboczy - metoda Fisenki.
- metoda graficzno-analityczna,
- używana m.in. przy projektowaniu zboczy kopalni odkrywkowych,
- I etap - ustalenie kształtu powierzchni poślizgu (najbardziej niekorzystną określa się na podstawie rozważa uzyskanych w teorii plastyczności,
- w gruntach spoistych powstają szczeliny pionowe,
- wyznacza się głębokość szczelin (H90)
![]()
- w warunkach równowagi granicznej powstają elementarne powierzchnie poślizgu, jeśli wartość naprężenia normalnego wynosi:
![]()
- konstrukcja Fisenki została wykonana dla F=1, dla innych wartości F przekształcono wzór
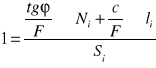
13. stateczność zboczy - metoda Masłowa.
- krzywoliniowa powierzchnia poślizgu,
- α - nachylenie zbocza (zmienne); kąt między poziomem a styczną do powierzchni zbocza,
- zbocze stateczne jeśli α = ψp
- zgodnie z równaniem Coulomba:
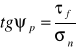
ψp = arctg(tgφ + ![]()
)
14. nośność podłoża uwarstwionego.
- warstwa słabonośna bezpośrednio pod fundamentem => przyjmujemy, że cały grunt zbudowany jest z materiału słabonośnego,
- warstwa słabonośna występuje na głębokości z ≤ 2B => sprawdzamy obciążenie graniczne w poziomie fundamentu zastępczego (jego podstawa leży na stropie utworów słabonośnych, B'=B+b, L'=L+b
15. nośność przy obciążeniu ukośnym lub mimośrodowym.
- wymiary fundamentu zredukowane są o wartość mimośrodu:
B'=B - 2eB
eB - mimośród działania obciążenia w kierunku równoległym do szerokości B,
L'=L - 2eL
eL - mimośród działania obciążenia w kierunku równoległym do długości L,
do wzoru na qf wstawia się dodatkowe współczynniki:
ic, id, ib - współczynniki wpływu nachylenia wypadkowej obciążenia od pionu wyznaczone z nomogramów.
16. rodzaje badań w aparacie trójosiowego ściskania.
UU - (unconsolidated, undrained) - bez konsolidacji, bez odpływu,
CD - (consolidated, drained) - po konsolidacji, z odpływem
CU - (consolidated undrained) - po konsolidacji, z odpływem
CI - konsolidacja izotropowa,
CA - konsolidacja anizotropowa,
K1 - σv rośnie, σh = const. (bez odpływu)
K2 - σv = const., σh maleje (bez odpływu)
K3 - σoct = const., σh maleje, σv rośnie (z odpływem)
E1 - σv maleje, σh = const. (z odpływem)
E2 - σv = const., σh rośnie, (z odpływem)
E3 - σoct = const., σh rośnie, σv maleje. (z odpływem)
17. model idealnie sztywnego ciała Euklidesa.
- ciało, które bez względu na wielkość i rodzaj działających na nie obciążeń nie odkształca się zupełnie,
równanie reologiczne:
εij = 0
18. model idealnie sprężystego ciała Hooke'a (H).
- nieważka sprężyna,
- odkształcenia proporcjonalne do naprężeń,
- po zdjęciu obciążenia odkształcenie = 0
równanie reologiczne
σij = σśr + τij
σśr = σkk = 3K*εkk
τij = 2G*υij
σij - tensor naprężenia
σśr - tensor kulisty stanu naprężeń (aksjator)
τij - dewiator naprężeń
K - moduł odkształcenia postaciowego
εkk - tensor kulisty odkształcenia
G - moduł odkształcenia objętościowego
υij - dewiator stanu odkształceń
19. model idealnie plastycznego ciała Saint-Venanta.
- odkształcenie ciała następuje po osiągnięciu granicy plastycznego płynięcia,
- po zdjęciu obciążenia odkształcenie pozostaje stałe.
równanie reologiczne:
τij = σpl
20. model idealnie lepkiej cieczy Newtona.
- przy stałym obciążeniu, prędkość odkształceń jest stała,
- po zdjęciu obciążenia odkształcenie pozostaje stałe
- charakteryzuje się liniową zależnością między τij i ![]()
ij
- poddana izotropowemu obciążeniu zachowuje się jak ciało Hooke'a,
- pod wpływem obciążenia odkształca się ze stałą prędkością,
- po zdjęciu obciążenia odkształcenie jest stałe.
równanie reologiczne:
σśr = σkk = 3K*εkk
τij = 2η*![]()
ij
![]()
- dewiator prędkości odkształcenia
η - współczynnik lepkości.
21. model lepko-sprężystego ciała Kelvina (lub Voigta) (K=H/N).
- ciało Kelvina charakteryzuje się opóźnioną w czasie sprężystością oraz brakiem relaksacji,
- przy stałym obciążeniu prędkość odkształceń dąży do zera,
- po zdjęciu obciążenia występuje pełzanie - stopniowy spadek odkształcenia do 0 z powodu lepkiego oporu cieczy N,
- połączenie równoległe ciała Hooke'a i cieczy Newtona.
równanie reologiczne:
τij = 2G*υij + 2η*![]()
ij
22. model sprężysto-lepkiej cieczy Maxwella.
- połączenie szeregowe ciała Hooke'a i cieczy Newtona,
- po przyłożeniu obciążenia ciało H odkształca się z prędkością dźwięku, następnie występuje odkształcenie cieczy N ze stałą prędkością odkształceń,
- po zdjęciu obciążenia ciało H wraca do odkształcenia 0, natomiast ciecz N pozostaje odkształcona,
równanie reologiczne:
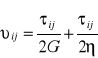
![]()
- dewiator prędkości zmian naprężenia
23. model ciała Binghama.
- połączenie szeregowe lub równoległe ciała Hooke'a, ciała Saint-Venanta i cieczy Newtona,
- charakteryzuje się własnościami sprężysto-plastyczno-lepkimi,
24. reologiczny model Kisiela.
- równolegle połączone modele Maxwella i Saint-Venanta,
- model ten umieszcza się w cylindrze z dziurkowanym tłokiem, czyli w cieczy Newtona,
25. ssanie gruntu.
- ssanie gruntu - ujemne ciśnienie w stosunku do zewnętrznego ciśnienia powietrza działającego na wodę zawartą w gruncie, któremu poddana jest ciecz o składzie identycznym do składu wody zawartej w gruncie,
- ssanie gruntu - sposób opisania zachowania gruntu nienasyconego poddanego zmianom zawilgocenia,
- całkowity potencjał ssania gruntu jest sumą potencjałów składowych:
ψ = ψg + ψm + ψs + ψp + ψt
ψg - potencjał grawitacyjny,
ψm - potencjał macierzysty,
ψs - potencjał osmotyczny,
ψp - potencjał gazowy,
ψt - potencjał temperaturowy.
W przybliżeniu ψ ≈ ψm = ua - uw
ua - ciśnienie powietrza [kPa]
uw - ciśnienie wody [kPa]
26. porównanie właściwości gruntów nasyconych i nienasyconych.
- grunty nienasycone - strefa aeracji,
- grunty nasycone - strefa saturacji,
- grunty nienasycone σzγ = σ'zγ, chyba, że występuje ssanie gruntu, wtedy σzγ < σ'zγ,
- grunty nasycone σzγ > σ'zγ, chyba, że występuje silny ruch wody w dół wtedy możliwe, że σzγ ≤ σ'zγ,
27. sprawdzić warunki równowagi dla stateczności dna wykopu.
28. metoda Felleniusa (parcie gruntu).
- założenia jak w metodzie Coulomba,
- powierzchnia poślizgu kołowo-cylindryczna,
- grunt spoisty, c ≠ 0, φ = 0.
Wyszukiwarka