Zagadnienia na egzamin z matematyki dla kierunku Budownictwo ( 2012 )

1. Definicja liczby zespolonej , jednostka urojona , sprzężenie liczby zespolonej , moduł i argument liczby zespolonej . Postać algebraiczna , trygonometryczna i wykładnicza liczby zespolonej .

Uzasadnić równości :

a)

b)
.

Obliczyć część rzeczywistą , urojoną i moduł liczby
.

Przedstawić w postaci trygonometrycznej liczbę
,
.

Rozwiązać równanie :
.

2. Macierz , macierz kwadratowa ,diagonalna , transponowana - określenia. Działania na macierzach - kiedy te działania można wykonać . Definicja macierzy odwrotnej do macierzy A - warunek istnienia macierzy odwrotnej .

Wykonać działania :

,
.

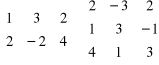
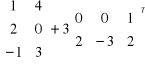
3. Definicja wyznacznika . Własności wyznaczników . Obliczanie wyznaczników - metoda Sarrusa i Laplace'a . Obliczyć wyznacznik stosując rozwinięcie Laplace'a : np.

,
.

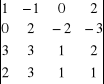
4. Układy równań liniowych . Podać Twierdzenie Cramera i Kroneckera-Capellego . Rozwiązać układ równań np.

,
,
.

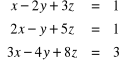
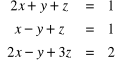
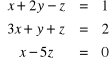
5. Iloczyn skalarny i wektorowy wektorów. Długość wektora .

Np. Obliczyć pole trójkąta rozpiętego na wektorach
i
.

6. Równanie płaszczyzny . Napisać równanie płaszczyzny np. przechodzącej przez punkt
i równoległej do płaszczyzny o równaniu
, …

7. Definicja ciągu ,granicy ciągu i własności granicy ciągu .

Np. obliczyć granice ciągów :
,
,
,

,
=
,
,
,

.

8. Definicja szeregu i jego zbieżności . Warunek konieczny zbieżności szeregu . Podać kryteria zbieżności szeregów o wyrazach dodatnich .

Np. zbadać zbieżność szeregów :
,
,
,
,
.

9. Pochodna funkcji - definicja , interpretacja geometryczna , własności pochodnej ( działania na pochodnych).

Podać warunki konieczny i wystarczający istnienia ekstremum funkcji .

Wyznaczyć przedziały monotoniczności i ekstrema funkcji : np.
,
,

,
,
,
,
.

10. Podać regułę de L'Hospitala . Obliczyć granicę : np.
,
,
,

.

11. Określenie funkcji pierwotnej .Związek całki oznaczonej nieoznaczonej .

Obliczyć całki : np.
,
,
,
,
,

,
,
,
,
.

Obliczyć pole obszaru płaskiego
ograniczonego krzywymi : a)
,
;

b)
,
, c)
,
,
.

12. Znaleźć ekstrema funkcji dwóch zmiennych :
;
;

,
. Podać warunek konieczny i wystarczający istnienia ekstremum lokalnego funkcji dwóch zmiennych .

13. Podać definicję równania różniczkowego i rozwiązania równania różniczkowego .

Sprawdzić , że funkcja
jest rozwiązaniem równania różniczkowego
.

14. Rozwiązać równanie różniczkowe … .

UWAGA : Podane tu zadania są tylko przykładami zadań , które mogą być na egzaminie

2

---