Doświadczenie losowe - takie doświadczenie, które może być powtarzane w zbliżonych warunkach i którego wyniku nie jesteśmy w stanie jednoznacznie przewidzieć.

Elementarne zdarzenie losowe - podstawowy, niepodzielny wynik danego doświadczenia losowego. Istnieją zdarzenia elementarne z określonym doświadczeniem. Trzeba bardzo dokładnie określić na czym polega nasze doświadczenie, sprecyzować warunki doświadczenia.

Zbiór wszystkich zdarzeń elementarnych naszego doświadczenia = przestrzeń zdarzeń.

Zdarzenie losowe - dowolny podzbiór zbioru elementarnego. Jeżeli przestrzeń zdarzeń jest nieprzeliczalna to zbiór zdarzeń losowych nie zawiera wszystkich jej podzbiorów. Def. Jest słuszna, gdy przestrzeń zdarzeń jest skończona lub co najwyżej przeliczalna.

Podzbiór - zbiór pusty = zdarzenie niemożliwe; lub taki, która zawiera wszystkie elementy tego zbioru = zdarzenie pewne.

Przeliczalny zbiór - równoliczne i majce tyle samo liczb, elementów, równoliczne ze zbiorem liczb rzeczywistych.

Definicja klasyczna prawdopodobieństwa wg Laplace z 1812 - jeśli przestrzeń zdarzeń, jakiegoś zdarzenia losowego, jakiegoś doświadczenia, zawiera n-jednakowo możliwych elementów to prawdopodobieństwo zdarzenia A zawierającego m z pośród tych elementów jest równe m/n:

, gdy n=0- to nie ma takiego rozwiązania, gdy n dąży do nieskończoności to zdarzenie jest nie możliwe by obliczyć prawdopodobieństwo. Definicja ta nadaje się gdy przestrzeń zdarzeń jest skończona.

Geometryczna def. prawdopodobieństwa - na niektóre zbiory nieskończone, które mają jakąś miarę, i którym możemy nadać geometryczna interpretację. Błąd logiczny nam nie znika.

Def. statystyczna (częściowa) - 1928, na podstawie doświadczenia (empirycznie); jeżeli w powtórzonym n-razy doświadczeniu, zdarzenie A występuje n_A-krotnie to prawdopodobieństwo tego zdarzenia jest równe granicy przy n dążącym do nieskończoności, z ułamka n_A/n.
; musimy rzucać nieskończenie wiele razy - niemożliwe do obliczenia; granica liczona empirycznie, więc nie da się udowodnić co się stanie, gdy zacznie np. wykres znów wariować - nie da się przewidzieć co będzie dalej.
, gdy n jest duże to można oszacować prawdopodobieństwo z matem. punktu widzenia.

Matematyczna def. prawdopodobieństwa = aksjometryczna def. prawdopodobieństwa - Kołomogorow, 1933; prawdopodobieństwo jest funkcją o wartościach rzeczywistych, której argumentami są zdarzenia losowe (elementarne).

1. Zawartości R tej funkcji spełniają warunek:
   

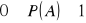
2. Prawdopodobieństwo zdarzenia pewnego jest równe 1 (zdarzenie o największym prawdopodobieństwie):
   

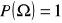
3. Jeżeli zdarzenia A₁, A₂, A₃,... itd. i jeżeli możemy je ponumerować to oznacza, że ten zbiór jest przeliczalny. Są zbiorami rozłącznymi, czyli nie mają żadnych, wspólnych elementów to wtedy prawdopodobieństwo sumy zdarzeń rozłącznych jest równe sumie prawdopodobieństw.

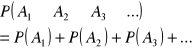
Zmienna losowa - dowolna funkcja o wartościach R, której argumentami są elementarne zdarzenia losowe. Oznacza się ją ostatnimi literami alfabetu łac. i dużymi literami: X,Y,Z, a małymi wartości zmiennych losowych, z, y, z. Mogą być:

Zmienne losowe dyskretne (skokowe) - zmienne, których zbiór wartości jest co najwyżej przeliczalny, przybiera skończoną liczbę wartości.

Zmienne losowe ciągłe - nie spełniają po wyższej def.

Rozkład prawdopodobieństwa = funkcja prawdopodobieństwa = funkcja rozkładu prawdopodobieństwa, dyskretnej zmiennej losowej p(x) jest równe prawdopodobieństwu X=x

Dystrybuanta - funkcja dystrybuanty, F jest określona na całym zbiorze liczb R. Wartość tej funkcji jest prawdopodobieństwem:
, przy czym
. Funkcja niemalejąca, bo
.
- zw. między dystrybuanta a f. Rosnącą

Parametry rozkładu zmiennej losowej:

1). Wartość przeciętna (oczekiwana) zmiennej losowej:

2). Wariancja - zmienność zmiennej losowej, jak bardzo odchylają się od wartości średniej: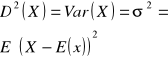

Odchylenie standardowe:

3). Moment zmiennej losowej

Moment rzędu k względem p. C zmiennej losowej X nazywamy wartość oczekiwaną z (X-c) do potęgi k. Gdzie k jest liczbą większą od 0, a c- dowolną l. R.

Momenty względem p. C=0 są momenty zwykłe. A momenty względem wartości p. C=E(x) to momenty centralne.

Moment zwykły to moment rzędu 1 i jest to wartość oczekiwana.

Moment centralny rzędu 2 -wariancja, a 3 rzędu miara asymetrii rozkładu.

Ciągłe zmienne losowe - zmienna losowa X jest ciągłą zmienną losową, jeśli dla dowolnych liczb a i b takich, że
i pewnej nieujemnej funkcji f zachodzi równość: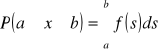
, gdzie f to funkcja gęstości rozkładu zmiennej losowej X.

- prawdopodobieństwo tego, że ciągła zmienna losowa przyjmuje dowolną, konkretną wartość jest równe zeru.

Prawdopodobieństwo tego, że ciągła zmienna losowa przyjmie wartość różną od dowolnej liczby, jest równe 1.

Wartość oczekiwana ciągłej zmiennej losowej X o gęstości f nazywamy całkę: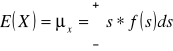

Wariancją ciągłej zmiennej losowej X o gęstości f nazywamy całkę: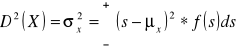

Nierówność Czebyszewa - jeśli X jest zmienną losową o wartości średniej μ i skończonej wariancji σ², to dla dowolnego ε>0:

Jeżeli ε = k* σ to

Statystyka opisowa - opis statystyczny danych; analiza zbiorów danych, które są tak duże, że rozmaitych powodów nie możemy ich badać w całości.

Estymatory - statystyki służące do szacowania wartości parametrów badanego obiektu (wartości generalnej) i w szczególności średnia arytmetyczna z próby jest estymatorem wartości oczekiwanej cechy populacji generalnej. Estymator jest dobry, gdy spełnia trzy kryteria.

1. Kryterium zgodności - jest zgodny, jeżeli przy n dążącym do nieskończoności prawdopodobieństwo tego estymatora będzie się różniło od dowolnej l. ε i to prawdopodobieństwo dąży do 0.
   

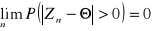
2. Kryterium nieobciążoności - jeżeli wartość oczekiwana tego estymatora będzie równa szacowanemu parametrowi to estymator jest nieobciążony.
   

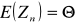
3. Kryterium efektywności - estymator jest tym lepszy im mniejszą ma wariancję. Estymatory różnią się efektywnością, co pozwala je poustawiać.

Nierówność Rao - Cramera - wartość estymatora nie może mieć mniejszej wariancji od wartości granicznej. Dla dowolnego, nieobciążonego, zgodnego parametru Θ wariancja jest mniejsza lub równa od ułamka: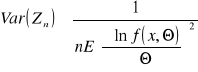

Gęstość normalnego rozkładu Gaussa -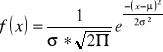

nie wykazuje 1 konkretnego rozkładu, ponieważ występuje jeszcze 2 parametry rozkładu.

Metoda momentu

Moment w próbie - pierwszy moment zwykły z próby
, moment centralny z próby
. Wariancja z próby:

Funkcja wiarygodności -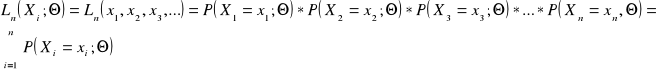

oszacowanie prawdziwej wartości parametru Θ przyjmujemy taką jego wartość, dla której ona osiąga maksimum.

dla rozkładów ciągłych

dla rozkładów skokowych

Estymatory przedziałowe - mają w założeniu zlikwidować wszelkie obawy, zamiast pojedynczych liczb znajdować przedziały

Estymacja punktowa - grupa metod statystycznych, służąca do punktowego oszacowania wartości szukanego parametru rozkładu. Punktowe oszacowanie oznacza tutaj, że uzyskujemy konkretną wartość liczbową.

Hipoteza statystyczna - dowolne (sensowne) przypuszczenie dotyczące postaci i/lub parametrów rozkładu badanej cechy w zbiorowości generalnej.

Hipoteza parametryczna - jeżeli hipoteza dotyczy tylko parametrów rozkładu o nieznanej postaci. Symbol Ω_p. Elementy zbioru Ω różnią się między sobą w najwyżej wartościami parametrów.

Hipoteza nieparametryczna - jeżeli elementy zbioru Ω różnią się między sobą nie tylko wartościami parametrów, ale i postacią funkcyjną rozkładu. Symbol Ω_n

Zbiór hipotez dopuszczalnych - zbiór wszystkich możliwych rozkładów, które mogą charakteryzować populację. Symbol: Ω.

Hipoteza prosta - gdy hipoteza parametryczna precyzuje dokładnie wartości wszystkich nieznanych parametrów rozkładu badanej cechy. Gdy zbiór ω jest jednoelementowy. Jednoznacznie wyznacza rozkład.

Hipoteza złożona - gdy zbiór ω jest wieloelementowy, niejednoznacznie wyznacza rozkład. Hipotezy nie są proste.

Test statystyczny - sposób postępowania (algorytm), umożliwiający weryfikację hipotezy na podstawie wyników próby losowej pobranej z badanej zbiorowości generalnej. Innymi słowy jest to algorytm rozstrzygający, jakie wyniki próby sugerują uznanie sprawdzonej hipotezy za prawdziwą, a jakie za fałszywą.

Hipoteza zerowa (H₀) - hipoteza weryfikowana; hipoteza, która poddajemy weryfikacji testem statystycznym.

Hipoteza alternatywna (H₁) - hipoteza konkurencyjna; hipoteza, która przyjmujemy w przypadku odrzucenia H₀.

Błąd I rodzaju - odrzucenie prawdziwej hipotezy zerowej. Prawdopodobieństwo popełnienia błędu I rodzaju nosi nazwę poziomu istotności testu (α).

Błąd II rodzaju - akceptacja fałszywej hipotezy zerowej. Prawdopodobieństwo popełnienia błędu II rodzaju oznaczamy przez β.

Moc testu (M) - prawdopodobieństwo nie popełnienia błędu II rodzaju.

Statystyka testowa - funkcja testowa; spodziewane wartości będą różne w zależności od tego, która z hipotez jest prawdziwa.

Zbiór krytyczny Λ - wartości sugerujące odrzucenie hipotezy zerowej.

Zbiór przyjęć Ψ - wartości sugerujące akceptację hipotezy zerowej.

Miary położenia - liczby odzwierciedlające przeciętną wartość badanej cechy ilościowej. To np. średnia arytmetyczna i mediana.

Miary zmienności - rozproszenia, rozrzutu; inf. o tym, w jakim stopniu poszczególne wartości koncentrują się wokół wartości przeciętnej. To np. odchylenie standardowe, odchylenie ćwiartkowe, współczynniki zmienności.

Odchylenie ćwiartkowe - oparte na tzw. statystykach pozycyjnych; opiera się na kwartylach: pierwszy kwartyl (Q₁) - wartość badanej cechy, że dla 25% elementów próby wartość tej cechy jest od Q₁ mniejsza i trzeci (Q₃) - odcina 75% najmniejszych wartości cechy.

Test zgodności χ² - sposób weryfikacji hipotezy o postaci rozkładu danych w populacji generalnej. Stosowana do wszelkiego rodzaju danych liczbowych.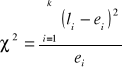

Przedział ufności - podstawowym narzędziem estymacji przedziałowej; przedział, który obejmuje rzeczywistą wartość badanego parametru z dowolnie dużym prawdopodobieństwem.

Współczynnik ufności - dowolnie duże dobierane prawdopodobieństwo; rzeczywista wartość parametru θ w populacji, która znajduje się w wyznaczonym przez nas przedziale ufności. Im większa wartość tego współczynnika, tym szerszy przedział ufności, a więc mniejsza dokładność estymacji parametru. Im mniejsza wartość 1 - α, tym większa dokładność estymacji, ale jednocześnie tym większe prawdopodobieństwo popełnienia błędu. Wybór odpowiedniego współczynnika jest więc kompromisem pomiędzy dokładnością estymacji a ryzykiem błędu. W praktyce przyjmuje się zazwyczaj wartości: 0,99; 0,95 lub 0,90, zależnie od parametru.

Wstępne przetworzenie danych - nadanie poszczególnym elementom badanej próby numerów porządkowych, zwanych rangami.

Współczynnik korelacji rangowej - współczynnik Spearmana; wykazuje monotoniczną zależność;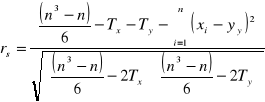
, gdzie T to poprawki na połączonych rangach, dane wyrażeniem: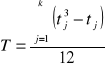
, gdzie k- ilość połączeń, a t_j- ilość rang łączonych przy i-tym połączeniu.

Korelacja - zależność liniową zmiennych losowych; siła związków między cechami.

Kowariancja
- liczba określająca zależność liniową między zmiennymi losowymi X i Y.
Regresja - metoda, pozwalająca na zbadanie związku pomiędzy różnymi wielkościami występującymi w danych i wykorzystanie tej wiedzy do przewidywania nieznanych wartości jednych wielkości na podstawie znanych wartości innych. Kształt zależności.

Współczynnik korelacji liniowej Pearsona określa poziom zależności liniowej między zmiennymi losowymi. Niech x i y będą zmiennymi losowymi o ciągłych rozkładach. x_i,y_i oznaczają wartości prób losowych tych zmiennych (i = 1,2,...,n), natomiast
- wartości średnie z tych prób.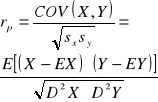

Spłaszczenie - współczynnik bezwymiarowy,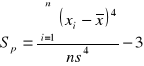

Test zgodności λ Komogorowa - wykazuje zgodność z rozkładem normalnym nawet dla danych odbiegających dużo od wartości normalnych. Opiera się na porównaniu zaobserwowanej w próbie empirycznej dystrybuanty (tzn. kumulanty) z dystrybuantą teoretyczną, wynikającą z weryfikowanejH₀.
, gdzie K(x_i) - to wartość dystrybuanty empirycznej obliczanej ze wzoru:
,a F(x_i) - dystrybuanta hipotetyczna (odczytywana z tablic danego rozkładu)

---