1997/1998	LABORATORIUM Z FIZYKI
ĆW. NR 65	TEMAT: BADANIE ROZKŁADU ELEKTRONÓW W ZALEŻNOŚCI OD ICH PRĘDKOŚCI
WYDZ. ELEKT KIER. E.L. i T. GRUPA 2	NAZWISKO I IMIĘ : Adam Korona Tomasz Janik
DATA WYKON.	OCENA		DATA ZALICZ.	PODPIS
21.04.1998	T
	S

1. Podstawa Pomiaru

Celem ćwiczenia jest określenie rozkładu termoelektronów w funkcji ich prędkości metodą hamującego potencjału. Badanie rozkładu elektronów w zależności od ich prędkości wykonujemy badając lampę elektronową.

Podając na anodę lampy próżniowej z żarzoną katodą napięcie hamujące przeszkadzające dopływowi elektronów do anody spowodujemy, że to do tej ostatniej dotrą tylko te elektrony, których energia kinetyczna jest większa od pracy sił pola elektrycznego wywołującego hamowanie. Mierząc prąd anody przy różnych napięciach hamowania, można bezpośrednio śledzić ilość termoelektronów zależności od ich energii (prędkości). Rysując wykres ln J_a w funkcji napięcia hamującego powinniśmy otrzymać prostą opisaną równaniem:

, gdzie

J_a0 - wartość natężenia prądu anodowego w przypadku gdy różnica potencjałów między anodą i katodą wynosi zero (U = 0);

U - wartość napięcia hamującego;

k_B - stała Boltzmana;

e - ładunek elementarny;

T - temperatura.

Znając e/k_BT (współczynnik nachylenia prostej) można obliczyć temperaturę odpowiadającą stanowi, w jakim znajduje się gaz elektronowy w lampie (wyznaczając temperaturę gazu elektronowego wyznaczamy temperaturę katody).

Znając wartość napięcia hamującego można określić prędkość elektronów korzystając z zależności:

, gdzie

m - masa elektronu;

v - prędkość elektronu;

e - ładunek elektronu.

2. Schemat Układu Pomiarowego

gdzie:

D - lampa elektronowa (dioda);

P - potencjometr;

R₁,R₂ - dekady rezystorowe;

mV - miliwoltomierz;

μA - mikroamperomierz;

A - amperomierz

3. Ocena Dokładności Pojedynczych Pomiarów

- Mikroamperomierz LE -1 :

klasa 0.5 zakres 750 [μA]

- Miliamperomierz LM -1:

klasa 0.5 zakres 1 [A]

- Woltomierz LM -1:

klasa 0.5 zakres 750 [mV]

4. Tabela Pomiarowe

I_Ż - prąd żarzenia; I_a - prąd anodowy;

4.1. Tabela zależności Ia od U dla kierunku przewodzenia

L.P	IŻ	Ia	U	IaRa	U'=U-IaRa	lnIa	lnIa/Iao
	[A]	[μA]	[mV]	[mV]	[mV]	Ia w [μA]
1	0.65	165	0	10	-10	5.11	0.004
2	0.65	210	50	13	37	5.35	0.24
3	0.65	250	100	15	85	5.52	0.41
4	0.65	290	150	18	132	5.67	0.56
5	0.65	335	200	20	180	5.81	0.70
6	0.65	380	250	23	227	5.94	0.83
7	0.65	430	300	26	274	6.06	0.95
8	0.65	475	350	28	322	6.16	1.05
9	0.65	525	400	32	368	6.26	1.15
10	0.65	580	450	35	415	6.36	1.25
11	0.65	620	500	37	463	6.43	1.32
12	0.65	680	550	41	509	6.52	1.41
13	0.65	735	600	44	556	6.60	1.49

4.2. Tabela zależności Ia od U dla kierunku zaporowego

L.P	IŻ	Ia	-U	IaRa	U'=U-IaRa	Ua=U'-ΔΦ	lnIa	lnIa/Iao
	[A]	[μA]	[mV]	[mV]	[mV]	[mV]	Ia w [μA]
1	0.65	165	0	9.9	-9.9	-37	5.11	0.004
2	0.65	125	50	7.5	-57.5	-85	4.83	-0.28
3	0.65	95	100	5.7	-105.7	-133	4.55	-0.56
4	0.65	65	150	3.9	-153.9	-181	4.17	-0.94
5	0.65	40	200	2.4	-202.4	-230	3.69	-1.42
6	0.65	30	250	1.8	-251.8	-279	3.40	-1.71
7	0.65	15	300	0.9	-300.9	-328	2.71	-2.40
8	0.65	10	350	0.6	-350.6	-378	2.30	-2.81
9	0.65	5	400	0.3	-400.3	-428	1.61	-3.50
10	0.65	2.5	450	0.2	-450.2	-478	0.92	-4.19
11	0.65	0	500	0	-500	-528	- ∝	-

4.3. Tabela wyników pomiarów

Dn/n0	Ek [meV]	V [km/s]
0,24 0,18 0,18 0,15 0,08 0,09 0,03 0,03 0,02 0.02	37 85 133 181 230 279 328 378 428 478	410 388 367 340 313 284 252 216 173 115

5. Przykładowe Obliczenia

R_a - rezystancja Mikromperomierza R_a = 60 [Ω]

- obliczanie wartości napięcia na mikroamperomierzu

• dla kierunku przewodzenia ( lp. 3 )

J_aR_a = 250 · 10^-6 · 60 = 15 mV

• dla kierunku zaporowego ( lp. 6 )

J_aR_a = 30· 10^-6 · 60 = 1.8 mV

- obliczanie napięcia na diodzie

• dla kierunku przewodzenia ( lp. 3 )

U' = U - J_aR_a = 100 - 15 · 10^-3 = 85 mV

• dla kierunku zaporowego ( lp. 6 )

U' = U - J_aR_a = -250 - 1.8· 10^-3 = -251.8mV

- obliczenie kontaktowej różnicy potencjałów Δϕ

Kontaktowa róznica potencjałow została wyznaczona na podstawie wykresu zależności

ln I_a/I_ao = f(U')

y = 0.0094 x + 0.3793

y = 0.0025 x + 0.188

porównując je otrzymujemy: Δϕ = - 0.1903/0.0069 = - 28 [mV]

- obliczanie rzeczywistego napięcia na diodzie (uwzględniając kontaktową różnicę potencjałów)

• dla kierunku zaporowego ( lp.6 )

U_a = U' +  = -251.8 + (-28) = - 279 mV

- obliczanie temperatury katody

tgα = 0.0094· 10³ = 9.4

k = 1.38· 10^-23 J/K

e = 1.6· 10^-19 c

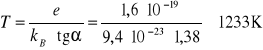
- obliczanie względnej liczby atomów

• dla kierunku zaporowego ( lp. 1 )

- obliczanie energii kinetycznej

• dla kierunku zaporowego ( lp.1 )

E_K = e · U_a

E_K = 1,6·10^-19 c · 37·10^-3 = 5,92·10^-21 [J]

- obliczanie prędkości elektronów

• dla kierunku zaporowego ( lp.1 )

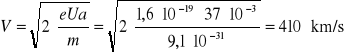
6. Rachunek Błędów

Błąd maksymalny pomiaru U'

U' = U - J_a· R_a stąd:

ΔU' = ΔU - Δ J_a· R_a

Δ J_a· R_a jest o rząd wielkości mniejsze od ΔU, więc wszystkie ΔU' są równe ΔU, czyli 4 [mV]

7. Zestawienie wyników

• Temperatura Katody

T = 1233 [K]

• Kontaktowa różnica potencjałów

Δϕ = - 28 [mV]

8. Wnioski i Spostrzeżenia

Zmniejszaniu się ilości termoelektronów towarzyszy wzrost ich energii kinetycznej, co obrazuje wykres zależności Δn/n₁ = f ( E_K ).

Metoda wyznaczenia kontaktowej różnicy potencjałów Δϕ obarczona jest dość dużym błędem ponieważ dokonuje się tego za pomocą odczytu z wykresu. Duży błąd odczytu wynikał mędzy innymi z tego, że proste aproksymujące nie przecinały się dokładnie na osi napięcia U'. Poza tym niemożliwość ikreślenia błędu maksymalnego odczytanej wartości Δϕ uniemożliwiła wyznaczenie błędu pomiarowego obliczonej wartości temperatury katody badanej lampy.

Obliczona na podstawie pomiarów temperatura katody wynosiła w przybliżeniu 1233 [K]. Jest to z pewnością wartość niezbyt dokładna, ale potwierdza słuszność rozkładu Maxwella - Blotzmana.

Doświadczenie cechuje się dużą niedokładnością. Wynika to z tego, że zbadanie E_k i v elektronu jest trudne ze względu na przypadkowy charakter wypływu elektronów z katody. Prędkości te możemy jedynie określić w pewnym przybliżeniu i z dość dużym błędem.

---