Sprawozdanie z ćwiczenia laboratoryjnego z Metrologii Temat : „Mostek odchyłowy” |
Sprawozdanie wykonał : Mieszko Mularczyk
Automatyka i Robotyka, rok III, grupa 1 Wydział Elektryczny, Politechnika Szczecińska |
1.Krótkie omówienie ćwiczenia. W tym ćwiczeniu badaliśmy nieliniowość mostka procentowego, oraz parametry na nią wpływające: rodzaje źródła zasilania (prądowe lub napięciowe), rodzaj miernika prądu stałego (woltomierz lub miliamperomierz), oraz wartości rezystorów składowych.
2.Schemat pomiarowy oraz opis przebiegu ćwiczenia. Schemat pomiarowy całego układu przedstawia się następująco:
Ro+ΔRx R2
R4=100Ω R3=100Ω
+ -
Jak widzimy, mamy do czynienia z typowym mostkiem procentowym. Pomiarów nieliniowości dokonaliśmy dla czterech różnych przypadków (4 serie pomiarowe):
źródło zasilania napięciowe, jako miernik woltomierz (U-U)
źródło zasilania napięciowe, jako miernik miliamperomierz (U-I)
źródło zasilania prądowe, jako miernik miliamperomierz (I-I)
źródło zasilania prądowe, jako miernik woltomierz (I-U)
Na samym początku ustawiliśmy dekady Ro oraz R2 na 100Ω, jednak mostek nie znajdował się w stanie równowagi (z obliczeń teoretycznych wynika, że powinien, ale należy wziąć pod uwagę niedokładność wszystkich rezystancji). Do stanu równowagi dla Ro=100Ω doprowadziliśmy mostek regulując wartość R2. Pomiarów dokonywaliśmy tak aby ΔRx zwiększało się w zakresie <0Ω - 100Ω> czyli aby względna zmiana rezystancji ε wynosiła od 0 do 1.
Wartość ε obliczamy ze wzoru:
Jednocześnie tak dostrajaliśmy źródło zasilania, aby dla ε=1 wartość odczytana napięcia wynosiła 1V (gdy miernikiem był woltomierz), lub odczytana wartość prądu 10mA (gdy miernikiem był miliamperomierz)
3.Tabele pomiarowe
W tabelach pomiarowych przyjęto następujące oznaczenia:
-względna zmiana rezystancji
ΔRx -bezwzględna zmiana rezystancji
W -wielkość mierzona (U lub I)
D -błąd nieliniowości mostka (różnica między wartością odczytaną W, a wartością w, która wynikałaby z liniowej charakterystyki mostka)
δn - względny błąd nieliniowości wyrażony w procentach:
przy czym Wmax wynosi 1V (gdy wielkością mierzoną jest napięcie) lub 10mA (gdy wielkością mierzoną jest prąd).
Seria pomiarowa 1 (U-U)
ΔRx [Ω] |
ε |
W [V] |
w [V] |
D=W-w [V] |
δn [%] |
10 |
0,1 |
0,143 |
0,100 |
0,043 |
4,3 |
20 |
0,2 |
0,272 |
0,200 |
0,072 |
7,2 |
30 |
0,3 |
0,391 |
0,300 |
0,091 |
9,1 |
40 |
0,4 |
0,500 |
0,400 |
0,100 |
10,0 |
50 |
0,5 |
0,600 |
0,500 |
0,100 |
10,0 |
60 |
0,6 |
0,692 |
0,600 |
0,092 |
9,2 |
70 |
0,7 |
0,778 |
0,700 |
0,078 |
7,8 |
80 |
0,8 |
0,857 |
0,800 |
0,057 |
5,7 |
90 |
0,9 |
0,931 |
0,900 |
0,031 |
3,1 |
100 |
1,0 |
1,000 |
1,000 |
0,000 |
0,0 |
Seria pomiarowa 2 (U-I)
ΔRx [Ω] |
ε |
W [mA] |
w [mA] |
D=W-w [V] |
δn [%] |
10 |
0,1 |
1,63 |
1,00 |
0,63 |
6,3 |
20 |
0,2 |
3,04 |
2,00 |
1,04 |
10,4 |
30 |
0,3 |
4,29 |
3,00 |
1,29 |
12,9 |
40 |
0,4 |
5,38 |
4,00 |
1,38 |
13,8 |
50 |
0,5 |
6,37 |
5,00 |
1,37 |
13,7 |
60 |
0,6 |
7,24 |
6,00 |
1,24 |
12,4 |
70 |
0,7 |
8,04 |
7,00 |
1,04 |
10,4 |
80 |
0,8 |
8,75 |
8,00 |
0,75 |
7,5 |
90 |
0,9 |
9,41 |
9,00 |
0,41 |
4,1 |
100 |
1,0 |
10,00 |
10,00 |
0,00 |
0,0 |
Seria pomiarowa 3 (I-I)
ΔRx [Ω] |
ε |
W [mA] |
w [mA] |
D=W-w [V] |
δn [%] |
10 |
0,1 |
1,43 |
1,00 |
0,43 |
4,3 |
20 |
0,2 |
2,72 |
2,00 |
0,72 |
7,2 |
30 |
0,3 |
3,91 |
3,00 |
0,91 |
9,1 |
40 |
0,4 |
4,99 |
4,00 |
0,99 |
9,9 |
50 |
0,5 |
5,99 |
5,00 |
0,99 |
9,9 |
60 |
0,6 |
6,92 |
6,00 |
0,92 |
9,2 |
70 |
0,7 |
7,77 |
7,00 |
0,77 |
7,7 |
80 |
0,8 |
8,57 |
8,00 |
0,57 |
5,7 |
90 |
0,9 |
9,31 |
9,00 |
0,31 |
3,1 |
100 |
1,0 |
10,00 |
10,00 |
0,00 |
0,0 |
Seria pomiarowa 4 (I-U)
ΔRx [Ω] |
ε |
W [V] |
w [V] |
D=W-w [V] |
δn [%] |
10 |
0,1 |
0,122 |
0,100 |
0,022 |
2,2 |
20 |
0,2 |
0,237 |
0,200 |
0,037 |
3,7 |
30 |
0,3 |
0,351 |
0,300 |
0,051 |
5,1 |
40 |
0,4 |
0,454 |
0,400 |
0,054 |
5,4 |
50 |
0,5 |
0,555 |
0,500 |
0,055 |
5,5 |
60 |
0,6 |
0,649 |
0,600 |
0,049 |
4,9 |
70 |
0,7 |
0,744 |
0,700 |
0,044 |
4,4 |
80 |
0,8 |
0,832 |
0,800 |
0,032 |
3,2 |
90 |
0,9 |
0,917 |
0,900 |
0,017 |
1,7 |
100 |
1,0 |
1,000 |
1,000 |
0,000 |
0,0 |
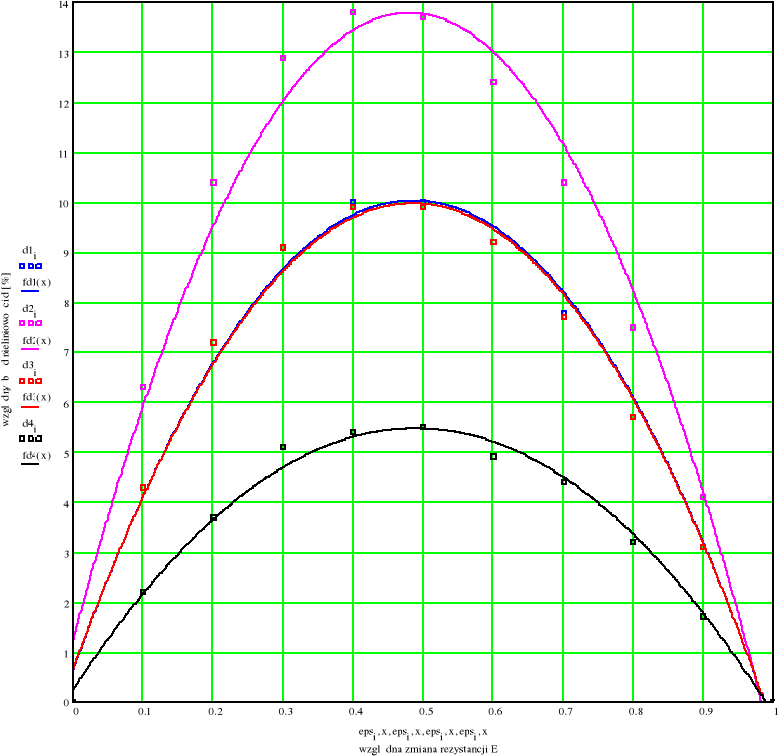
Dla obliczonych wartości względnego błędu nieliniowości δn (w każdej serii pomiarowej) sporządzamy wykres funkcji δn=f(ε), aby obrazowo porównać wpływ rodzaju zasilania oraz użytego miernika.
4.Wykres δn=f(ε)
Legenda:
---- seria pomiarowa 1 (U-U)
---- seria pomiarowa 2 (U-I)
---- seria pomiarowa 3 (I-I)
---- seria pomiarowa 4 (I-U)
Uwagi dotyczące wykresu: Dla każdej serii pomiarowej nanieśliśmy punkty pomiarowe, oraz dokonaliśmy aproksymacji wielomianowej (wielomian stopnia 2 - parabola) metodą najmniejszych kwadratów. Jak widzimy funkcje aproksymujące nie przechodzą przez punkt 0, wynika to z błędów pomiarowych (punkty nie są usytuowane symetrycznie względem prostej ε=0,5 - nie tworzą idealnej paraboli)
Wniosek: Z wykresu wnioskujemy, że najmniejszy błąd nieliniowości, mamy wtedy gdy źródłem zasilania jest źródło prądowe, a przyrządem pomiarowym jest woltomierz (obydwa urządzenia mają duży opór wewnętrzny), zaś największy błąd nieliniowości występuje, gdy źródłem zasilania jest źródło napięciowe, a przyrządem pomiarowym jest miliamperomierz (obydwa urządzenia mają bardzo mały opór wewnętrzny). Wpływ wszystkich rezystancji w obwodzie (w tym rezystancji zasilacza oraz miernika) na nieliniowość mostka zostanie wyjaśniony w następnym punkcie.
5.Analiza wpływu rezystancji w obwodzie na nieliniowość mostka.
Funkcję przetwarzania mostka procentowego możemy zapisać ogólnie:
gdzie:
W - wartość odczytana z miernika
- względna zmiana rezystancji Ro
α - współczynnik proporcjonalności (zależny od wartości wielkości zasilającej)
β - współczynnik nieliniowości mostka procentowego
Analizując wzór na funkcję przetwarzania mostka, dochodzimy do wniosku, że aby mostek był jak najbardziej liniowy to parametr β musi być jak najbliższy 0.
Wartość parametru β określamy zgodnie ze wzorem:
gdzie rezystancja Rw jest rezystancją widzianą z zacisków tak jak na rysunku poniżej:
Ro Rw Ro
mRo mRo
gdzie m - stała (w naszym ćwiczeniu wynosiła 1)
Jak widzimy, dla m=1, parametr β przyjmie następujące wartości, w zależności od rodzaju źródła zasilania oraz miernika (numeracja tak jak dla serii pomiarowych):
(U-U)
(U-I)
(I-I)
(I-U)
Wniosek: Z rozważań teoretycznych potwierdza się fakt, że najkorzystniejsza sytuacja (najmniejsza nieliniowość - najmniejszy współczynnik β) występuje wtedy, gdy mostek zasilamy źródłem prądowym, a jako miernik stosujemy woltomierz. Dodatkowo zauważamy, że dla sytuacji 1 oraz 3 współczynnik β wynosi 0,5 - czyli wykresy względnego błędu nieliniowości dla serii pomiarowych 1 i 3 powinny się pokrywać (tak nie jest - wynika to z błędów pomiarowych). Ważnym czynnikiem wpływającym na tę niedokładność jest fakt, że założyliśmy, że woltomierz i źródło prądowe mają nieskończenie dużą rezystancję (w rzeczywistości mają skończoną), oraz to, że miliamperomierz oraz źródło napięciowe mają rezystancję równą 0 (w rzeczywistości jest ona większa od 0)
6.Sposoby zmniejszenia nieliniowości mostka.
Z wcześniejszych rozważań wiemy, że nieliniowość mostka procentowego jest najmniejsza, gdy obwód zasilamy źródłem prądowym, a miernikiem jest woltomierz. Jednak zauważamy (zgodnie ze schematem z poprzedniej strony), że współczynnik β zależy również od rezystancji R3 i R4 (mRo) znajdujących się w obwodzie. Wtedy wzór na ten współczynnik dla połączenia I-U (sytuacja nr 4) będzie się przedstawiał następująco:
stąd widzimy, że zwiększając te rezystancje możemy obniżyć nieliniowość mostka. W dalszej części ćwiczenia połączyliśmy obwód taki jak w serii pomiarowej 4, zwiększając wartości rezystancji R3 i R4 100-krotnie (do wartości 10kΩ), wtedy współczynnik β wyniesie 1/202. Następnie ponownie dokonaliśmy pomiaru nieliniowości mostka (w sposób taki sam jak poprzednio - w serii pomiarowej nr 4).
Tabela pomiarowa (I-U)
ΔRx [Ω] |
ε |
W [V] |
w [V] |
D=W-w [V] |
δn [%] |
10 |
0,1 |
0,1007 |
0,1000 |
0,0007 |
0,07 |
20 |
0,2 |
0,2012 |
0,2000 |
0,0012 |
0,12 |
30 |
0,3 |
0,3017 |
0,3000 |
0,0017 |
0,17 |
40 |
0,4 |
0,4018 |
0,4000 |
0,0018 |
0,18 |
50 |
0,5 |
0,5019 |
0,5000 |
0,0019 |
0,19 |
60 |
0,6 |
0,6019 |
0,6000 |
0,0019 |
0,19 |
70 |
0,7 |
0,7017 |
0,7000 |
0,0017 |
0,17 |
80 |
0,8 |
0,8013 |
0,8000 |
0,0013 |
0,13 |
90 |
0,9 |
0,9007 |
0,9000 |
0,0007 |
0,07 |
100 |
1,0 |
1,0000 |
1,0000 |
0,0000 |
0,00 |
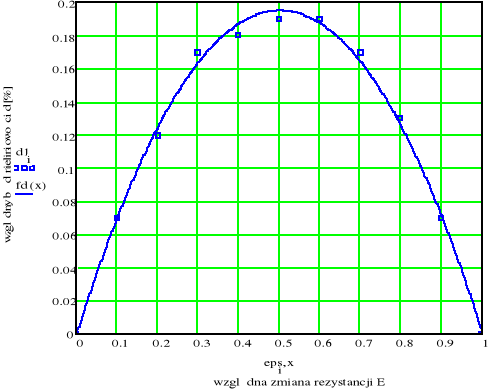
Dla pomierzonych wartości sporządzamy wykres δn=f(ε), tak jak to już czyniliśmy poprzednio.
Wykres δn=f(ε)
Wniosek: Tak jak na poprzednim wykresie obserwujemy to, że punkty pomiarowe układają się w kształt paraboli (odchyłki od prostej aproksymującej są spowodowane niedokładnościami pomiarowymi). Jednak w tym przypadku obserwujemy względny błąd nieliniowości mniejszy o rząd wielkości od poprzedniego (m=1).
Uwagi końcowe: Jak to już zostało opisane we wnioskach w całym opracowaniu, na nieliniowość mostka mają wpływ wartości rezystancji znajdujących się w obwodzie. Najkorzystniejszą sytuację (mała nieliniowość) uzyskujemy wtedy gdy źródłem zasilania jest źródło prądowe, a miernikiem woltomierz. Dodatkowo większe wartości rezystancji R3 i R4 również wpływają na obniżenie nieliniowości mostka.
Dodatkowo w ramach ćwiczenia przebadaliśmy działanie gotowego (fabrycznie zmontowanego) mostka procentowego, służącego do pomiaru odchyłek rezystancji od wartości wzorcowej. W tym celu przebadaliśmy małą populację rezystorów, które były oznakowane tolerancją ±5%.
Poniżej zamieszczono tabelę pomiarową:
L.p. |
Odchyłka badanego rezystora od wartości podanej przez producenta [%] |
1 |
-2,5% |
2 |
-0,1% |
3 |
0,0% |
4 |
-2,5% |
5 |
-3,0% |
6 |
-1,5% |
7 |
-2,5% |
8 |
-0,5% |
9 |
-4,0% |
10 |
-0,5% |
11 |
-2,0% |
12 |
-1,0% |
Wniosek: Jak widzimy wszystkie badane rezystory mieszczą się w zakresie tolerancji ±5%.
miernik prądu stałego
zasilacz prądu stałego (prądowy lub napięciowy)
![]()
![]()
![]()
![]()
Z
M
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka