a drugie zapiszemy następująco

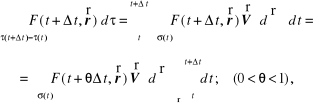
uprzednio określając przyrost
w postaci (rozdz. 3.4)

i stosując twierdzenie o wartości średniej

Po wykorzystaniu uzyskanych rezultatów i twierdzenia Gaussa-Ostrogradskiego (12.32) ostatecznie otrzymamy

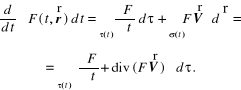
(12.68)

R*wnanie ciąg*ości . Masa płynu zawarta w obszarze płynnym τ wynosi

po zastosowaniu wzoru (12.64) możemy więc zasadę zachowania masy wyrazić następująco

(12.69)

Obszar τ został wybrany całkowicie dowolnie, musi więc znikać funkcja podcałkowa - stąd otrzymamy równanie ciągłości w postaci różniczkowej (3.17).

Po wykorzystaniu wzorów (12.22), (12.64) i (12.65) możemy wyznaczyć tzw. pochodn* hydrodynamiczn*

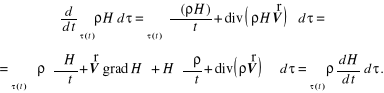
(12.70)

R*wnania ruchu ośrodka ci*g*ego. Ich wyprowadzenie polega na zastosowaniu zasady zachowania pędu. Obliczając więc pęd

oraz siły masowe

i siły powierzchniowe

gdzie
jest tensorem naprężenia lepkiego (8.1) ÷ (8.3), zapisujemy zasadę zachowania pędu w postaci

(12.71)

i następnie po wykorzystaniu wzorów (12.66) oraz (12.32) ostatecznie mamy

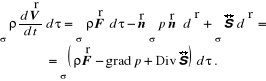
(12.72)

Równanie ruchu dla płynu lepkiego Newtona uzyskamy przyjmując następujący związek konstytutywny

(12.73)

gdzie
jest tensorem kulistym (o składowych

- tensorem prędkości de-formacji (12.59), zawierającym wielkości (3.25).

R*wnanie zachowania energii wynika z pierwszej zasady termodynamiki (8.18)

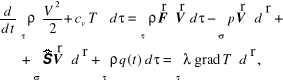
(12.74)

po uwzględnieniu zmiany energii w obszarze τ, mocy sił mechanicznych (masowych i powierzchniowych), mocy źródeł ciepła i mocy dostarczonej przez przewodnictwo cieplne. Dokonując takich samych przekształceń jak w równaniu (12.71) ostatecznie uzyskujemy

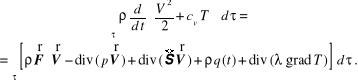
(12.75)

12.5. Wsp**rz*dne krzywoliniowe ortogonalne

W niektórych zastosowaniach wygodnie jest posługiwać się odpowiednio dobranymi układami współrzędnych, najczęściej są to układy ortogonalne.

Współrzędne krzywoliniowe
określa się zadając układ trzech funkcji różniczkowalnych

(12.76)

których jakobian jest różny od zera i nieskończoności lub zadając układ funkcji odwrotnych

(12.77)

Punkty w przestrzeni wyznaczone są zatem przez podanie wartości parametrów
linie współrzędnych są natomiast krzywymi będącymi przecięciem się dwu, spośród trzech nierównoległych powierzchni

Pochodne wektora-promienia
względem współrzędnych krzywoliniowych

(12.78)

są wektorami stycznymi do linii współrzędnych
Bazowe wektory jednostkowe są więc określone zależnościami

(12.79)

zawierającymi współczynniki

(12.80)

noszące nazwę współczynników Lamego .

W układzie wektorów bazowych (12.79) wektor
można zapisać w postaci

(12.81)

w której wielkości
są składowymi fizycznymi wektora
Wynika stąd, że nieskończenie małe przyrosty
wzdłuż linii współrzędnych są określone następująco

(12.82)

a kwadrat odległości dwu nieskończenie bliskich punktów jest równy

(12.83)

gdzie

(12.84)

gdyż

na podstawie wzoru o zamianie zmiennych w wyrażeniach różniczkowych.

W układzie ortogonalnym pochodne wektora-promienia
spełniają relacje

(12.85)

Różniczkujemy każdą z tych relacji względem współrzędnej, która nie występuje w niej explicite:

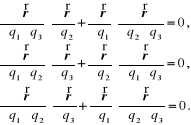
Po dodaniu dwóch kolejnych uzyskanych zależności i wykorzystaniu pozostałej otrzymamy:

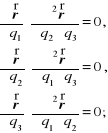
zatem jest

i następnie na mocy równości

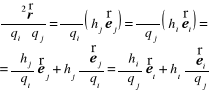
mamy

(12.86)

Różniczkując z kolei ilorazy wektorowe bazowych wektorów jednostkowych:

uzyskujemy związki

(12.87)

*

Składowa gradientu ϕ w kierunku i-tej współrzędnej jest definiowana jako przyrost pola skalarnego ϕ na jednostkę długości w tym kierunku, a zatem

i następnie

(12.88)

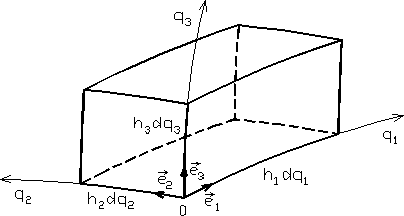
Rys. 12.11

W celu obliczenia diwergencji rozważymy nieskończenie mały prostopadłościan krzywoliniowy (rys. 12.11), którego trzy krawędzie leżą na liniach współrzędnych i mają długości
objętość prostopadłościanu wynosi zatem

(12.89)

Postępując tak samo jak w rozdziale 12.2, obliczamy zmianę strumienia pola wektorowego
w kierunku 2

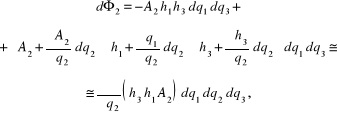
a następnie uwzględniając łączny wypływ przez ścianki rozważanego prostopadłościanu, gdy średnica jego objętości dąży do zera, otrzymujemy

(12.90)

Dla wyznaczenia składowej
obliczamy cyrkulację wektora
w płaszczyźnie

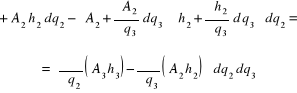
oraz jego cyrkulację w pozostałych płaszczyznach przez przestawienie cykliczne. Ostateczny wynik można przedstawić za pomocą wyznacznika

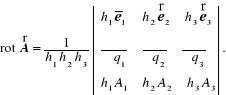
(12.91)

Korzystając z tożsamości (12.25) oraz wzorów (12.84) i (12.89) otrzymamy wyrażenie na laplasjan pola skalarnego

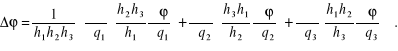
(12.92)

Na podstawie wzoru (12.88) można łatwo zauważyć, że operator
jest zdefiniowany we współrzędnych krzywoliniowych ortogonalnych następująco

(12.93)

Przy jego wykorzystaniu można przez bezpośrednie różniczkowanie obliczyć diwegencję i rotację wektora
w postaci (12.81):

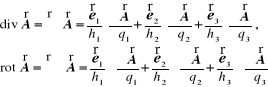
oraz pochodną konwekcyjną
występującą we wzorze na przyspieszenie elementu płynu (3.11). Biorąc pod uwagę zależności (12.86) i (12.87) dla pochodnych wektorów jednostkowych względem współrzędnych krzywoliniowych

otrzymamy

(12.94)

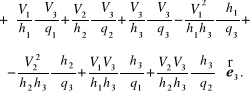
Powyższą zależność można również uzyskać za pomocą tożsamości udowodnionej w przykładzie 4.1.

W podobny sposób można obliczyć gradient wektora
(12.81)

(12.95)

oraz diwergencję tensora

(12.96)

Po wykonaniu wszystkich operacji różniczkowania oraz wykorzystaniu związków (12.86) i (12.87) otrzymamy:

(12.97)

oraz dla tensora symetrycznego

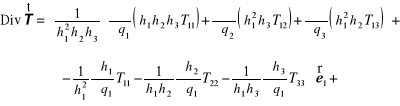
(12.98)

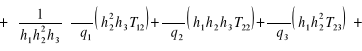
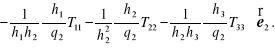
(12.98cd.)

*

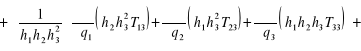
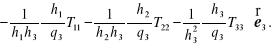
Zapiszemy teraz operatory różniczkowe (12.88), (12.90) ÷ (12.92) oraz równania ruchu cieczy lepkiej dla
w postaci różniczkowej wynikającej z (12.72)

(12.99)

we współrzędnych walcowych i współrzędnych kulistych.

Z porównania wzorów (12.47) i (12.58) otrzymujemy zależność

(12.100)

z której w oparciu o wzory (12.97) mamy:

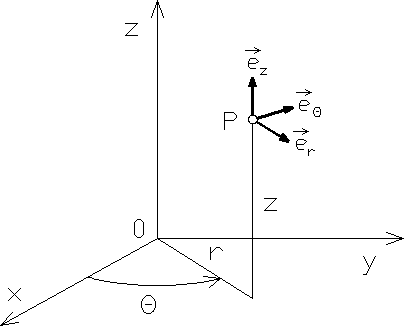
Rys. 12.12

W przypadku układu współrzędnych walcowych
przedstawionego na rys. 12.12, wzory (12.77) mają postać:

za ich pomocą obliczamy

skąd wynika:

i następnie otrzymujemy:

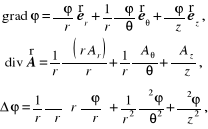
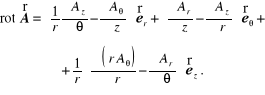
Po obliczeniu składowych tensora deformacji (12.100):

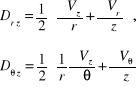
i następnie przy wykorzystaniu wzoru (12.98) oraz równania ciągłości
równania Naviera-Stokesa (12.99) ÷ (12.100) przybierają postać:

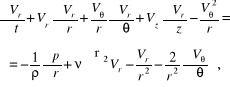
Rys. 12.13

Zgodnie z rys. 12.13 współrzędne kuliste są określone zależnościami:

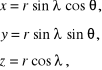
zatem

Znając współczynniki Lamego

łatwo wyznaczamy wszystkie operatory różniczkowe:

oraz składowe tensora deformacji
(12.100):

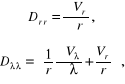
W układzie współrzędnych kulistych równania ruchu cieczy lepkiej stanowią układ równań:

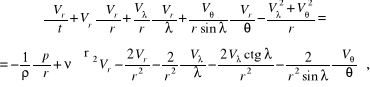
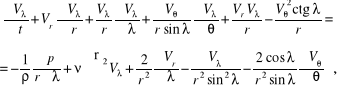
366

---