Wydział Budowy Maszyn i Informatyki Bielsko - Biała, 16.03.2010

Rok akademicki: 2009/2010

Studia: stacjonarne/inż.

Semestr: 4

Kierunek/Specjalność: ZiIP

Grupa: Wtorek - godz. 14.15-16.00

LABORATORIUM

METROLOGII TECHNICZNEJ

Laboratorium nr 4

Niepewność pomiaru w pomiarach pośrednich

Wykonali:

Sprawozdanie
Do poprawy:
Zaliczone:

NIEPEWNOŚĆ POMIARU W POMIARACH POŚREDNICH

Celem kolejnych ćwiczeń w laboratorium metrologii było przypomnienie podstawowych pojęć związanych z niepewnością pomiaru, omówienie zależności, że pomiar jest dwuelementowy oraz stwierdzenia mówiącego, że niepewność pomiaru zależy od strategii pomiaru. Oprócz samego wyjaśnienia tych zależności przedstawiono wyznaczenie złożonej niepewności pomiaru w pomiarach pośrednich, tym samym sposób posługiwania się przyrządami mikrometrycznymi, odczytywanie wskazań przez interpolację z dokładnością 0,001 mm przez dobór odpowiednich końcówek pomiarowych i wymiana trzpieni pomiarowych w głębokościomierzu.

WSTĘP TEORETYCZNY

BŁĄD POMIARU
= wartość zmierzona - wartość rzeczywista

Do pomiarów kątów, nachyleń i stożków stosuje się:

- uniwersalne przyrządy pomiarowe mechaniczne i sprzęt pomocniczy, jak kątomierze

uniwersalne, kątowniki nastawne, liniały sinusowe, skośnice sinusowe, kątomierze z

poziomicami, przyrządy czujnikowe, kulki i wałeczki pomiarowe,

- uniwersalne i specjalne przyrządy optyczne, jak kątomierze optyczne, optyczne

poziomice kątowe, głowice podziałowe optyczne, stoły podziałowe, mikroskopy

warsztatowe, goniometry, teodolity.

Wśród metod pomiarowych rozróżnia się:

- metody bezpośrednie,

- metody pośrednie.

Niepewność pomiaru - jest związana z rezultatem pomiaru parametrem, który charakteryzuje rozrzut wyników i może być w uzasadniony sposób przypisany wartości mierzonej.

Sposób obliczania niepewności zależy od charakteru pomiaru. Wyróżnia się dwie zasadnicze metody:

1. Ocena niepewności metodą typu A dotyczy określania niepewności pomiaru drogą analizy statystycznej serii wyników pomiarów.

Zatem niepewność standardowa oceniana metodą typu A jest zdefiniowana jako odchylenie standardowe średniej.

2. Ocena niepewności metodą typu B dotyczy określania niepewności pomiaru drogą inną niż metoda A tzn. wówczas gdy nie mamy do czynienia z serią wyników lub gdy w serii wyników nie występuje rozrzut.

W metodzie tej niepewność standardową określa się na podstawie rozkładu prawdopodobieństwa możliwych wyników pomiarów znanego, bądź założonego przez eksperymentatora.

Źródłem wiedzy o rozkładzie mogą być:

• Specyfikacja dostarczona przez producenta przyrządu,

• Wcześniejsze dane pomiarowe,

• Ogólna wiedza o zachowaniu i własnościach określonych materiałów i instrumentów,

• Niepewności przypisane danym pochodzącym z podręczników.

NIEPEWNOŚĆ STANDARDOWA POMIARÓW POŚREDNICH

Z pomiarami pośrednimi mamy do czynienia, gdy dokonuje się pomiarów bezpośrednich kilku wielkości x1, x2, …,xk , a następnie na ich podstawie wyznacza wielkość y określoną przez związek funkcyjny:

y = f(x1, x2, …, xk)

Metody określania niepewności pomiarowych:

1. Niepewność standardowa pomiarów bezpośrednich

Przypuśćmy, że wykonaliśmy serię n pomiarów bezpośrednich wielkości fizycznej X otrzymując wyniki X₁, X₂ ...X_n. Jeśli wyniki pomiarów nie są takie same, wówczas za najbardziej zbliżoną do wartości prawdziwej przyjmujemy średnią arytmetyczną ze wszystkich wyników pomiarów:

(1)

Stwierdzenie to jest tym bardziej słuszne im większa jest liczba przeprowadzonych pomiarów (dla
,
). W celu określenia niepewności standardowej posługujemy się w tym wypadku sposobem typu A, czyli korzystamy ze wzoru na odchylenie standardowe średniej

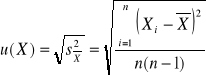
(2)

Jeśli natomiast wyniki pomiarów nie wykazują rozrzutu, czyli
, lub też gdy istnieje tylko jeden wynik pomiaru, wówczas niepewność standardową szacujemy sposobem typu B. Można np. wykorzystać informację o niepewności maksymalnej
określonej przez producenta przyrządu pomiarowego, jeśli nie mamy innych dodatkowych informacji, wówczas niepewność standardową obliczamy ze wzoru

(3)

Dla prostych przyrządów (tj. linijka, śruba mikrometryczna czy termometr) jako
można przyjąć działkę elementarną przyrządu. W elektronicznych przyrządach cyfrowych niepewność maksymalna podawana jest przez producenta w instrukcji obsługi i jest zwykle kilkakrotnie większa od działki elementarnej. Najczęściej zależy ona od wielkości mierzonej X i zakresu na którym mierzymy Z:

Gdy występują oba typy niepewności (tzn. zarówno rozrzut wyników jak i niepewność wzorcowania) i żadna z nich nie może być zaniedbana (tzn. obie są tego samego rzędu), wówczas niepewność standardową (całkowitą) obliczamy ze wzoru

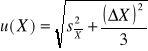
. (4)

2. Niepewność standardowa pomiarów pośrednich - niepewność złożona (u_c)

W przypadku pomiarów pośrednich wielkość mierzoną Y obliczamy korzystając ze związku funkcyjnego, który można zapisać w ogólnej postaci:
, gdzie symbolami
oznaczamy k wielkości fizycznych mierzonych bezpośrednio. Zakładamy, że znane są wyniki pomiarów tych wielkości
oraz ich niepewności standardowe
. Wynik (końcowy) pomiaru oblicza się wówczas ze wzoru:

W przypadku pomiarów pośrednich nieskorelowanych (tzn. gdy każdą z wielkości
mierzy się niezależnie) niepewność złożoną wielkości Y szacujemy przy pomocy przybliżonego wzoru:

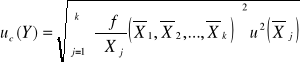
(5)

3. Niepewność rozszerzona

Niepewność standardowa całkowicie i jednoznacznie określa wartość wyniku, jednak do wnioskowania o zgodności wyniku pomiaru z innymi rezultatami (np. z wartością tabelaryczną) oraz dla celów komercyjnych i do ustalania norm przemysłowych, zdrowia, bezpieczeństwa itp. Międzynarodowa Norma wprowadza pojęcie niepewności rozszerzonej oznaczanej symbolem U (dla pomiarów bezpośrednich), lub U_c (dla pomiarów pośrednich). Wartość niepewności rozszerzonej oblicza się ze wzoru

lub
(6)

Liczba k, zwana współczynnikiem rozszerzenia, jest umownie przyjętą liczbą wybraną tak, aby w przedziale
znalazła się większość wyników pomiaru potrzebna dla danych zastosowań. Wartość współczynnika rozszerzenia mieści się najczęściej w przedziale 2-3. W większości zastosowań zaleca się przyjmowanie umownej wartości
.

Wałeczki pomiarowe - są wzorcami końcowymi, które średnice odtwarzają wzorcowe wymiary. Znajdują zastosowanie w pomiarach średnic podziałowych gwintów zewnętrznych, niektórych parametrów kół zębatych, kątów stożków zewnętrznych, promieni łuków, itp. Komplet wałeczków pomiarowych do gwintów stanowi 21 trójek wałeczków o średnicach od 0,17 do 6,35 mm.

Produkuje się również wałeczki do pomiaru kół zębatych. Komplet stanowią 23 pary wałeczków o wymiarach Pd 1-7 do 17 mm.

Kulki pomiarowe - wzorce miary w postaci wykonanych z dużą dokładnością kulek (zwykle wybiera się je spośród kulek do łożysk tocznych). Kulki pomiarowe stosowane są do pomiaru średnic podziałowych gwintów wewnętrznych, do pomiaru średnic otworów itp.

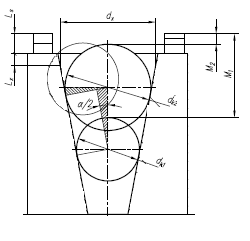
Pomiar kąta stożka wewnętrznego kulkami i głębokościomierzem.

Pomiar wykonuje się metodą pośrednią dwiema, różnymi metodami, odpowiednio 

dobranymi kulkami pomiarowymi oraz głębokościomierzem mikrometrycznym.

Pomiar stożka za pomocą kul pomiarowych.

Pomiar przeprowadza się metodą pośrednią. Oprócz kul pomiarowych
używa się głębokościomierza mikrometrycznego, którym mierzy się
długości pomiarowe M1 i M2, a niekiedy również płytek wzorcowych.

W celu wyznaczenia kąta stożka należy wykorzystać zależność
wynikającą z wyróżnionego na trójkątnego.

Pomiar stożka za pomocą wałeczków pomiarowych.

Pomiar jest metodą pośrednią. Oprócz wałeczków pomiarowych używa
się płytek wzorcowych i mikrometru, którym mierzy się długości
pomiarowe M1 i M2.

OBLICZENIA WRAZ Z PODSTAWIENIAMI

1. Pomiar kąta stożka zewnętrznego:

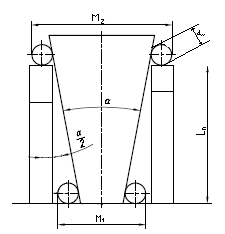
Pomiar I

Długość stosu płytek: L_n1 = 20mm

g

Długości płytek składowych w stosie 1 [mm]	Długości płytek składowych w stosie 2 [mm]
10	20
9,5
0,5

Odchyłki graniczne ± te w stosie 1 [µm]	Odchyłki graniczne ± te w stosie 2 [µm]
0,2	0,3
0,2
0,2

Średnica wałeczka: d_w = 7,2

Pomiary: M₁ = 46,179 mm

M₂ = 53,132 mm

Obliczenia:

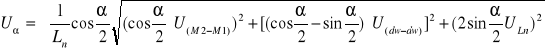
; L - mierzona długość w mm

; n - liczba płytek w stosie

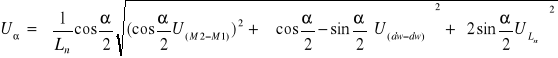
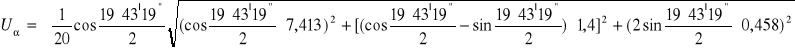
α = 19°43'19'' ±

Pomiar II

Długość stosu płytek: L_n1 = 20mm

Długości płytek składowych w stosie 1 [mm]	Długości płytek składowych w stosie 2 [mm]
30	50
20
Odchyłki graniczne ± te w stosie 1 [µm]	Odchyłki graniczne ± te w stosie 2 [µm]
0,4	0,4
0,3

Średnica wałeczka: d_w = 7,2mm

Pomiary: M₁ = 46,179mm

M₂ = 63,296mm

Obliczenia:

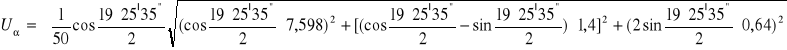
α =
±

2. Pomiar stożka zewnętrznego mikroskopem pomiarowym:

Dla
oraz
:

Przód:

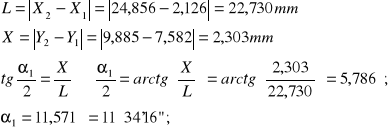
Niepewność pomiarowa

A=5; B=
C=

A=5; B=
C=

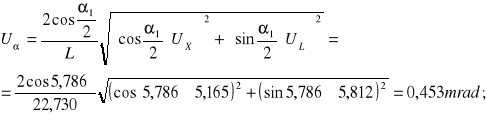
Tył:

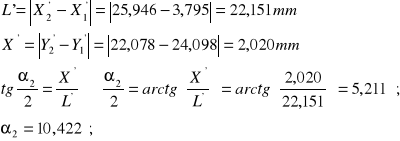
Dla
oraz
:

Przód:

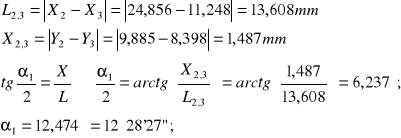
Niepewność pomiarowa

A=5; B=
C=

A=5; B=
C=

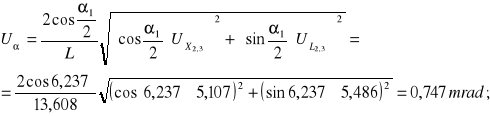
Tył:

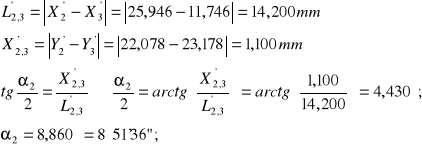
3. Pomiar kąta stożka wewnętrznego:

Średnica kuli [mm]	dk1=19.054	dk2=20.511	dk3=27.449
Pomiar [mm]	M1=40,428	M2=35,635	M3=17,019

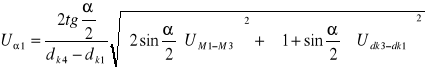
; L - mierzona długość w mm

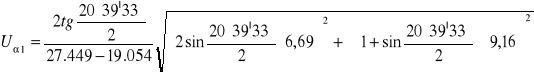
α₁ =
±

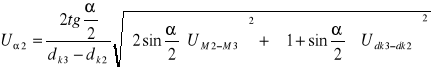
; L - mierzona długość w mm

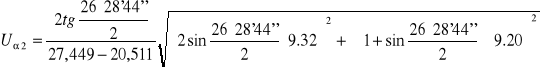
α₂ = 26°28'44'' ± 2°48'54''

WNIOSKI

Po wykonaniu ćwiczenia i przeanalizowaniu otrzymanych wyników można stwierdzić, że pomiar za pomocą wałeczków okazał się najmniej dokładnym. Duży błąd spowodowany jest niedokładnością przyrządu mierniczego oraz błędne odczyty z przyrządu. Wynika on również z nierównomiernego przylegania końcówek mierniczych do wałeczków jak również wałeczki mogą posiadać błędy kształtu.

---