1. Zamień jednostki:

3	mm	=	……………	dm	12	m	=	……………	km
21	cm	=	……………	m	5	km	=	……………	mm
2	ha	=	……………	m^2	100	cm^2	=	……………	dm^2
4	l	=	……………	cm^2	15	m^2	=	……………	mm^2
99	dm^2	=	……………	cm^2	162	a	=	……………	mm^2

2. Oblicz promień okręgu:

1. opisanego na trójkącie równobocznym o boku długości 10 cm.

2. wpisanego w trójkąt równoboczny o boku długości 15 cm.

3. wpisanego w romb o boku długości 7 cm i kącie ostrym 30^o.

4. opisanego na sześciokącie foremnym o boku długości 4 cm.

5. wpisanego w sześciokąt foremny o boku długości 6 cm.

6. opisanego na trójkącie równobocznym o boku długości 12cm.

7. opisanego na trójkącie prostokątnym o przyprostokątnych długości 4cm i 10cm.

3. Na trójkącie prostokątnym równoramiennym opisano okrąg o promieniu 4cm. Oblicz pole trójkąta.

4. Oblicz stosunek pola koła wpisanego do pola koła opisanego na trójkącie równobocznym.

5. Oblicz promień okręgu wpisanego w trójkąt równoboczny, którego boki mają długość 12cm.

6. Pole powierzchni całkowitej sześcianu jest równe 54cm2. Oblicz objętość tego sześcianu.

7. Pole powierzchni sześcianu jest równe 96cm2. Oblicz długość przekątnej sześcianu.

8. Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 6cm.

9. Przekątna ściany sześcianu ma długość 8cm. Oblicz pole powierzchni i objętość tego sześcianu.

10. Oblicz pole powierzchni i objętość prostopadłościanu, którego krawędzie maja długość 3cm, 2cm, 4cm.

11. Oblicz długość przekątnej prostopadłościanu o bokach 3cm, 4cm, 2cm.

12. W prostopadłościanie przekątne sąsiednich ścian bocznych są nachylone do podstawy pod kątami 30^o i 60^o. Oblicz pole powierzchni i objętość tego prostopadłościanu, jeżeli jego wysokość ma 6cm.

13. Prostopadłościan ma w podstawie kwadrat. Przekątna tego prostopadłościanu ma długość 4cm i jest nachylona do podstawy pod kątem 60^o. Oblicz pole powierzchni całkowitej i objętość tego prostopadłościanu.

14. 
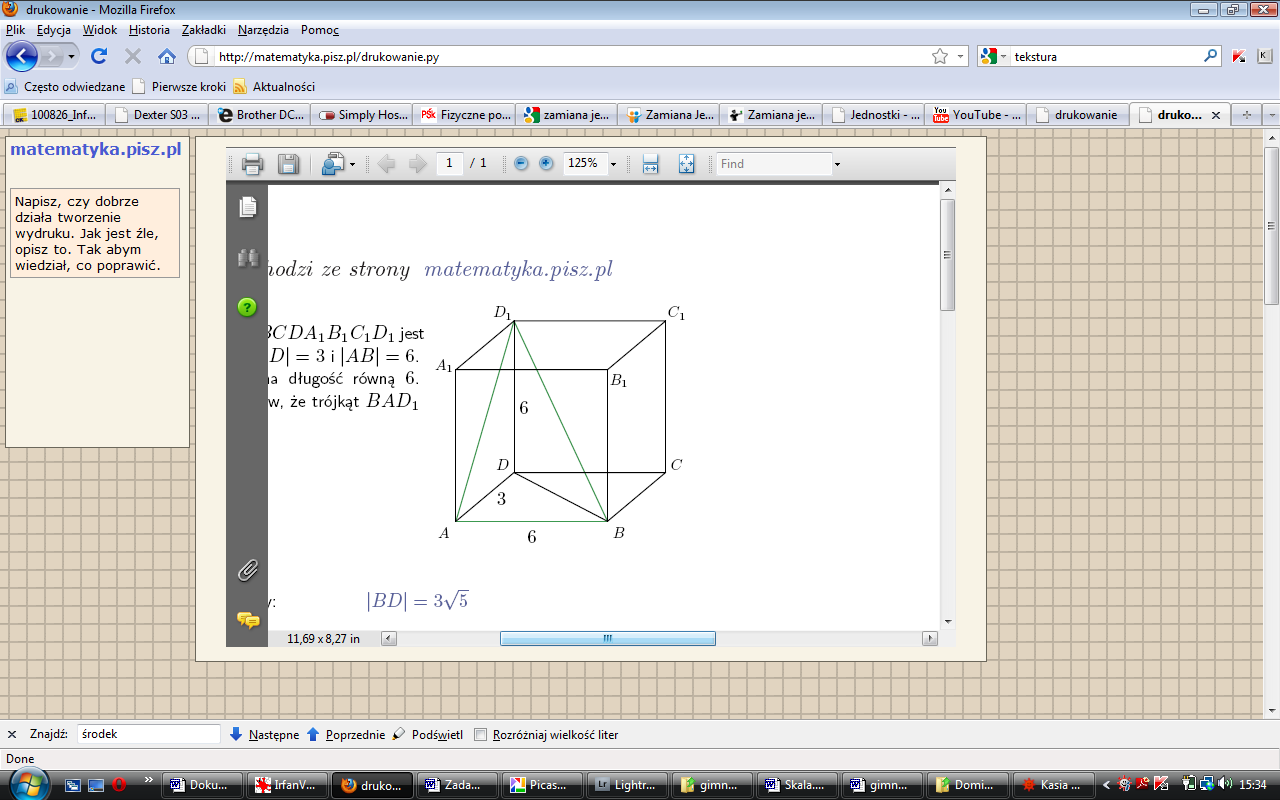
    Podstawa prostopadłościanu ABCDA₁B₁C₁D₁ jest prostokąt o bokach długości: |AD| = 3 i |AB| = 6. Wysokość prostopadłościanu ma długość równą 6. Uzasadnij, za pomocą rachunków, ze trójkąt BAD₁ jest prostokątny.

15. W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma 6cm a wysokość 5cm. Oblicz pole powierzchni i objętość tego ostrosłupa.

16. W ostrosłupie prawidłowym trójkątnym ściany boczne są nachylone do podstawy pod kątem 60^o. Wysokość ścian bocznych ma długość 4cm. Oblicz pole powierzchni i objętość tego ostrosłupa.

17. W ostrosłupie prawidłowym trójkątnym krawędzie boczne, których długość to 12cm, są nachylone do podstawy pod kątem 30^o. Oblicz pole powierzchni i objętość tego ostrosłupa.

18. Oblicz pole podstawy, powierzchni bocznej, powierzchni całkowitej i objętość czworościanu foremnego, którego krawędź ma długość 2cm.

19. Oblicz wysokość czworościanu foremnego, którego krawędź ma długość a.

20. Podstawa ostrosłupa jest trójkąt prostokątny, którego przyprostokątne maja długość 2cm i 4cm. Z wierzchołka kąta prostego tego trójkąta wychodzi pod katem prostym krawędź boczna ostrosłupa o długości 6cm. Oblicz pole powierzchni i objętość ostrosłupa.

---