FIZYKA CIAŁA STAŁEGO

WYKŁADY

DYNAMIKA SWOBODNEGO PUNKTU MATERIALNEGO

Podstawowe równanie dynamiki zwane dynamicznym równaniem różniczkowym ruchu swobodnego punktu materialnego ma postać:

równanie ruchu punktu materialnego możemy zapisać w postaci wyrażenia wskazującego na zmienność siły

gdzie

- wektor wodzący, określający położenie punktu materialnego

- wektor prędkości

- czas w którym porusza się punkt materialny.

PIERWSZE ZADANIE DYNAMIKI (proste)

W pierwszym zadaniu mechaniki należy wyznaczyć wartość i kierunek wypadkowy sił działających na punkt materialny znając masę punktu i jego równania ruchu. Trzeba więc wyznaczyć przyśpieszenie, różniczkując względem czasu równania ruchu.

Jeżeli ruch punktu jest opisany wektorem, promieniem wodzącym

wówczas przyśpieszenie

według drugiego prawa Newtona siła działająca na omawiany punkt jest równa

w przypadku, gdy ruch punktu jest opisany we współrzędnych prostokątnych za pomocą równania skalarnego :

to rzut wypadkowej
wszystkich sił działających na punkt materialny wynoszą

ze wzorów:

obliczamy wartość i kierunek wypadkowej siły F.

DRUGIE ZADANIE DYNAKIKI (odwrotne)

Drugie zadanie dynamiki polega na wyznaczeniu równań ruchu punktu materialnego znając jego masę i działające siły.

Zadanie to sprowadza się do całkowania równań różniczkowych ruchu.

Jeżeli w chwili początkowej znane będzie położenie punktu i rzuty prędkości tego punktu to wtedy równania początkowe dla t=t₀ są następujące

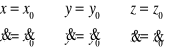
Siła
może być funkcją czasu t, położenia
i prędkości
punktu co możemy zapisać :

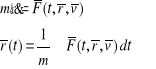
Zasada d'Alemberta dla punktu materialnego, zgodnie z drugim prawem Newtona

Możemy sprowadzić do postaci

Powyższe równanie możemy rozpatrywać jako warunek równowagi siły
przyłożonej do punktu materialnego M i wektora
będącego siłą fikcyjną.

Siłą bezwładności lub siłą d'Alemberta nazywamy fikcyjną siłę
, równą co do wartości iloczynowi masy i przyśpieszenia punktu materialnego lecz przeciwnie do tego przyśpieszenia skierowaną.

Siła d'Alemberta

Zasada d'Alemberta

Na punkt materialny M działają siły rzeczywiste, które w każdej chwili równoważą się z siłą bezwładności tego punktu.

Składowe siły bezwładności w prostokątnym układzie Oxyz wynoszą

Z równania
wynikają następujące równania różniczkowe ruchu punktu materialnego

BEZWŁADNOŚCIOWY UKŁAD ODNIESIENIA

Nazywany jest układem Galileusza, nieinercjalnym lub absolutnym

Jest to układ w którym obowiązują prawa Newtona. Parametry ruchu ciała ( prędkość, przyśpieszenie) zależą od układu odniesienia, względem którego będzie dany ruch obserwowany. Dlatego należy ustalić jaki układ możemy nazwać absolutnym.

W dynamice bezwładnościowy układ odniesienia ( układem, w którym obserwujemy prawa Newtona) będzie układ sztywno związany z Ziemią. Ponieważ wartość przyspieszenia kuli ziemskiej jest bardzo mała w porównaniu z wartością przyspieszenia grawitacyjnego.

Grawitacja

Galileusz jest postacią ściśle związaną z rozwojem mechaniki. Stwierdził, że wszystkie ciała materialne na Ziemi spadają z równym przyspieszeniem g. Czyli niezależnie od wielkości czy rodzaju ciała
. Wektor
jest zawsze skierowany do środka Ziemi i nazywany przyśpieszeniem ziemskim. Wartość tego przyśpieszenia zależy od wysokości nad poziomem morza i szerokości geograficznej miejsca na ziemi, w którym ciało spada.

Np. na biegunie g=9,83 m/s a na równiku g=9,78 m/s.

Przypadek rzutu ukośnego.

Równanie ruchu w układzie xy przyjmują postać

całkując je dwustronnie otrzymujemy

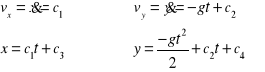
Stałe całkowania c₁ i c₂ wyznaczamy z warunków początkowych dla ciała t₀=0

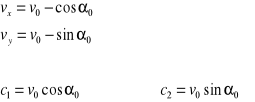
możemy zapisać, że

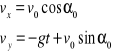
stałe całkowania c₃ i c₄ wyznaczamy z warunków początkowych dla t=0, x=0, y=0

- znajdujemy więc c₃ =0 i c₄=0

Równanie ruchu ciała

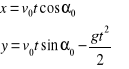
Równanie toru otrzymujemy po usunięciu z powyższych dwóch równań ruchu parametru t, a więc:

Torem ciała o masie M wyrzuconego pod kątem
do poziomu z prędkością
jest parabola o osi pionowej, zwrócona wypukłością w górę. Na podstawie równania toru znajdziemy zasięg rzutu, odległość na jaką spadnie ciało od miejsca, z którego został wyrzucony:

największa wysokość rzutu h, na którą wzniesie się ciało określimy ze wzoru:

PĘD PUNKTU MATERIALNEGO, ZASADA ZACHOWANIA PĘDU

Pędem lub ilością ruchu punktu materialnego M nazywam wektor, równy iloczynowi masy i prędkości, mający kierunek i zwrot prędkości.

Pęd - wektor skierowany wzdłuż stycznej do toru.

Dynamiczne równanie ruchu Newtona
może przyjąć nieco inną postać. Przyśpieszenie
punktu materialnego jest równe :

więc

Masa jest stała tzn. niezależna od czasu, zatem zgodnie z drugim prawem Newtona pochodna pędu wynosi:

z powyższego wynika, że pochodna pędu względem czasu rozpatrywanego punktu materialnego równa jest sumie sił działających na ten punkt.

Równanie
zapisujemy w postaci:

a następnie całkujemy w przedziale odpowiadającym czasom t₂ i t₁:

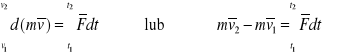
Jest to równanie wyrażające zasadę pędu punktu materialnego, zaś wyrażenie
nazywamy impulsem siły.

Zasada pędu punktu materialnego.

Geometryczny przyrost pędu w określonym przedziale czasu równa się popędowi sił działających w tym czasie.

Zasada zachowania pędu punktu materialnego.

Jeżeli na punkt materialny działa układ sił pozostający w równowadze, to pęd punktu materialnego jest wektorem stałym.

jeżeli
.

Zasada krętu punktu materialnego.

Pochodna względem czasu krętu
punktu materialnego, obliczonego względem nieruchomego bieguna O, jest równa momentowi wypadkowej sił działających na badany punkt materialny względem tego bieguna.

Kąt pomiędzy wektorem prędkości i wektorem pędu jest równy 0 czyli :

zatem

ponieważ iloczyn wektorowy
jest równy momentowi
wypadkowej siły
względem bieguna O to równanie
będzie wyrażać zasadę krętu punktu materialnego

W przypadku, gdy na punkt materialny działa suma geometryczna sił czynnych i reakcji to moment jest równy sumie geometrycznej momentów tych sił

Zasada zachowania krętu punktu materialnego

Jeżeli moment wypadkowej sił punktu materialnego względem dowolnego bieguna O jest równy zero, to kręt punktu materialnego względem tego bieguna jest stały.

Czyli jeżeli

to

rzutując powyższe równanie na osie współrzędnych O_x, O_y, O_z otrzymujemy

PRACA ELEMENTARNA

Pracą elementarną nazywamy iloczynem skalarnym siły
działającej na punkt materialny M, który przemieszcza się w dowolny sposób po torze od punktu A do B

gdzie F - wartość siły

ds - przemieszczenie, przyrost współrzędnej łukowej

- kąt między kierunkiem siły
i wektorem stycznym do toru

Więc pracę zapisujemy

gdy

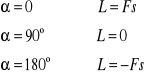
wynika z tego, że wartość pracy może być dodatnia lub ujemna.

Praca siły ciężkości działającej na punkty materialne jest iloczynem tej siły i różnicy poziomów położenia A i położenia B.

Punkt M pod wpływem siły ciężkości

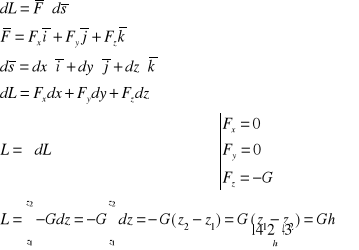
Praca sił sprężystości

Na ciało wywołujące rozciąganie działa siła sprężyny
, której wydłużenie równe jest
. Siła ta jest równa

gdzie k - współczynnik proporcjonalności zwany stałą sprężyny.

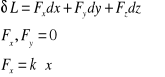
praca elementarnej siły F_x na przemieszczeniu dx

praca siły F_x na skończonym przemieszczeniu ( od 0 do x₁)

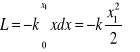
Praca w polu sił

Polem sił nazywamy przestrzeń na której znajduje się punkt materialny pod działaniem ściśle określonej siły zależnej tylko od położenia punktu.

Punkt materialny M poruszający się po torze AB

Praca punktu materialnego M zależy od toru po którym się porusza, przechodząc z położenia A do położenia B.

W celu określenia pola sił podajemy funkcje położenia:

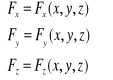
Polem sił możemy nazwać linie charakteryzujące się tym, że są styczne w każdym punkcie do wektora siły

Jednorodne pole sił jest to pole, w którym linie pola sił są prostymi równoległymi, siły dla wszystkich punktów są stałe co do kierunku i wartości, czyli każdemu punktowi odpowiada taka sama siła ( np. pole ciężkości w pobliżu ziemi ).

Prace wykonaną przez pole sił wyliczymy ze wzoru

Pole potencjalne (zachowawcze)

To przestrzeń, w której działa siła
niezależna od toru, lecz od położenia początkowego i końcowego.

Potencjałem siły
jest funkcja trzech zmiennych, które określają wartość pracy zależnie od położenia początkowego i końcowego.

Jeżeli siła
zależy tylko od położenia i istnieje taka funkcja pola Φ (x, y, z)zwana potencjałem siły, że:

to pacę obliczamy ze wzoru:

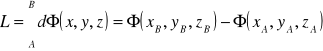
Funkcję symetryczną do potencjału nazywamy energią potencjalną:

UKŁAD PUNKTÓW MATERIALNYCH

Układ punktów materialnych to zbiór punktów, którym przypisane są pewne masy. Położenia każdego punktu są zależne od położenia innych punktów, podobnie oddziaływania między nimi.

Rozróżniamy układy punktów swobodnych i nieswobodnych

Układ punktów swobodnych to układ punktów materialnych, który nie jest ograniczony więzami i zależny jest tylko od początkowych wartości i od oddziaływań.

Układ punktów nieswobodnych to układ punktów, których ruch jest ograniczony więzami.

Każdy punkt może być opisany za pomocą trzech współrzędnych.

W układzie punktów materialnych mamy do czynienia z siłami wewnętrznymi i zewnętrznymi.

Wszystkie siły wewnętrzne zgodnie z III zasadą Newtona tworzą w układzie układ sił przeciwnych. Zaś siły zewnętrzne są siłami czynnymi działającymi na punkty materialne danego układu, pochodzącymi od działania innego układu niewchodzącego w skład układu badanego.

Środek masy układu punktów materialnych

Położenie każdego punktu materialnego Ni o skupionej, skończonej masie Mi określa promień - wektor
poprowadzony z obranego bieguna.

Środkiem masy punktu o masie mn (nieskończonej) nazywamy punkt geometryczny c, którego wektor spełnia równanie:

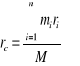
gdzie, M=

We współrzędnych kartezjańskich, rzutując powyższe równania wektorowe na osie otrzymujemy:

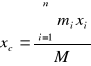
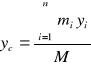
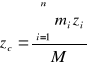
Momenty pierwszego rzędu (momenty statyczne) to:

;
;

x_c, y_c, z_c - określają współrzędne środka masy

Zasada ruchu środka masy:

Środek masy układu punktów materialnych porusza się jak swobodny punkt materialny, w którym skupiona jest masa układu.

DYNAMIKA BRYŁY SZTYWNEJ

Moment bezwładności bryły sztywnej to granica, do której dąży suma iloczynów mas elementarnych kwadratu odległości tych elementów (mas) od osi.

- od osi 2

- od punktu O

- na płaszczyźnie OXY

TWIERDZENIE STEINERA

W XIX w. Szwajcarski matematyk udowodnił, że moment bezwładności ciała sztywnego względem dowolnej osi równy jest sumie momentów bezwładności względem osi przechodzącej przez środek masy oraz iloczynu masy ciała i kwadratu odległości między tymi dwiema osiami.

Tarcza

Pręt

;

DYNAMICZNE RÓWNANIA RUCHU BRYŁY SZTYWNEJ

Dynamiczne równania ruchu potęgowego bryły sztywnej

Dynamiczne równanie ruchu obrotowego

Dynamiczne równanie ruchu płaskiego.

Dynamiczne równania ruchu płaskiego

Zad. 1 Korzystając z dynamicznych równań ruchu wyznaczyć przyspieszenie podnoszonego ciężaru o masie m₁ znajdującego się na końcu linki przerzuconej przez krążek o promieniu r₂ i masie m₂ i zaczepionej do ciała trzeciego masie m₃. Dany jest również współczynnik tarcia - f

I.

II.

III.

Równania więzów:

Energia kinetyczna b. szytwnej w ruchu postępowym

- wektor prędkości liniowej

Energia kinetyczna b. sztywnej w ruchu obrotowym

ω

Wartość prędkości dowolnego punktu ciała

gdzie:

ostatecznie:

Energia kinetyczna b. sztywnej w ruchu obrotowym równa jest połowie iloczynu momentu bezwładności bryły względem osi obrotu i kwadratu prędkości kątowej.

Energia kinetyczna b. sztywnej w ruchu płaskim

Tw. Younga

Energia kinetyczna w ruchu płaskim bryły sztywnej równa jest sumie energii kinetycznej b. sztywnej w ruchu postępowym środka masy i energii kinetycznej w ruchu obrotowym wokół osi przechodzącej przez środek masy i prostopadłej do płaszczyzny kierującej ruchu płaskiego.

Bryła sztywna w układzie płaskim.

moment bezwłądności bryły względem prostej przechodzącej przez środek masy

Energia kinetyczna w ruchu kulistym b. sztywnej.

Wyrażamy jako połowę iloczynu momentu bezwładności b. sztywnej względem chwilowej osi obrotu i kwadratu chwilowej prędkości kątowej.

Energia kinetyczna w ruchu dowolnym bryły sztywnej.

Ruch dowolny bryły sztywnej możemy rozważać jako ruch złożony z ruchu postępowego względem masy i ruchu wokół chwilowej osi obrotu.

Zasada równowartości energii kinetycznej i pracy bryły sztywnej.

Mówi ona, że przyrost energii kinetycznej bryły sztywnej na pewnym przesunięciu jest równy sumie prac sił zewnętrznych czynnych i reakcji na tym przesunięciu.

w chwili końcowej w chwili początkowej

Moc siły

Mocą siły nazywamy pracę wykonaną w ciągu jednostki czasu.

Moc chwilowa

przyrost pracy wykonany w tym czasie

określony przedział czasu

Moc w ruchu postępowym

Jeżeli w ruchu postępowym pracę dL zapiszemy jako
i podstawimy do wzoru na moc, wówczas moc tej siły wynosi:

Moc siły jest więc iloczynem skalarnym wektora siły F i wektora prędkości v punktu przyłożenia.

Jeżeli kierunek sił pokrywa się z kierunkiem prędkości to:

Moc siły w ruchu obrotowym

M

Tor punktu materialnego

h

l

x

V₀

M

x

y

z

M

O

B

A

M

ds

x₁

y₁

x₂

x₂

z₂

z₁

B

M

A

z

y

x

A

A

X₁

X

y

Siły zewnętrzne

Siły wewnętrzne

z

Mi

B

M

A

z

y

x

x

mn

Mc

y

x

z

y

x

z

Φ

r

Położenie dowolnego elementu bryły sztywnej

M

O

y

x

z

C

z₁

d

O

m

r

y

x

z

z

l

C

m

O

z

y

x

A₁

A₂

C

A_c

dm

h

O

Z

x

y

z

C

α

m₃

m₁

T₃₂

T₂₃

T₁₂

T₂₁

III

II

I

Dane: m₁, r₂, m₂, m₃

T₁₂

x

Kierunek ruchu ciała

m₁g

m₁

T₂₁

T₂₃

φ

α

x₃

T₃₂

R

m₃a₃

α

m₃g

T

m₃g*cosα

m₃g*sinα

R= m₃g*cosα=0

T = f*N = f* m₃g*cosα

M₁

M₂

M_s

M_i

c

M_i

c

π

M

0

c

---