LOGIKA

Zdaniem w sensie logicznym nazywamy stwierdzenie, któremu można przyporządkować określoną wartość logicznych.

Wartość logiczną zdania opisuje funkcja przynależności do zbioru A.

Logika formalna, klasyczna zajmuje się tylko zdaniami orzekającymi.

p, f(x), g(x,y), - symbole zdań logicznych.

p, q, r - nazywamy zdaniami atomowymi, prostymi.

Logika wielowartościowa.

Dwuwartościowa	w: A -> { 0,1 }	Logika klasyczna, Boole'a
Trzywartościowa	w: A -> { 0,1, ⊥}
n-wartościowa	w:A -> {0,1,...,n }	Skale ocen
Rozmyta (FUZZY)	w: A -> [ 0,1 ]	Logika ciągła, probabilistyka

Jan Łukaszewicz 1920 wielowartościowe logiki

Emil L. Post 1921 dodatkowe stopnie „prawdy”

K. Gödel 1932 logika pośrednia

Lotfi Zadeh 1965 logika rozmyta

Logika rozmyta (fuzzy logic), jedna z logik wielowartościowych stanowi uogólnienie klasycznej dwuwartościowej logiki. Jest ściśle powiązana z teorią zbiorów rozmytych i teorią prawdopodobieństwa. Została zaproponowana przez Lofti Zadeha w 1965 roku. W logice rozmytej między stanem 0 (fałsz) a stanem 1 (prawda) rozciąga się przedział wartości pośrednich, które można kojarzyć z prawdopodobieństwem.

Logika dwuwartościowa: Wartości logiczne:

• Wyrażenie p=1 jest skrótem; p jest prawdziwe, wartością logiczną zdania p jest prawdą,

• Wyrażenie p=0 jest skrótem, zdanie p jest fałszywe, wartością logiczną zdania p jets fałsz.

Z logiki dwuwartościowej wynika prawo wyłącznego środka

Spójniki zdaniowe - funktory zdaniotwórcz

• nieprawda, że” (∼),

• „i” (∧),

• „lub” (∨),

• „jeżeli, to” (=>),

• „wtedy i tylko wtedy, gdy” (),

• „albo” (∨)

Klasyczny rachunek zdań:

• Alternatywa p lub q p∨q

• Koniunkcja p i q p∧q

• Implikacja jeśli p to q p=>q

• Równoważność p wtedy i tylko wtedy pq

• Negacja nie p ∼p

• Dysjunkcja p albo q; p|q

nie p lub nie q p∨q

Tabela wartości logicznych:

p	q	p∨q	p∧q	p=>q	pq	p|q	∼p
1	1	1	1	1	1	0	0
1	0	1	0	0	0	1	0
0	1	1	0	1	0	1	1
0	0	0	0	1	1	1	1

Prawa rachunku zdań

1. podwójnego przeczenia ∼(∼p)p

2. łącznej koninkcji (p∧q)∧rp(q∧r)

3. łącznosci alternatywy (p∨q)∨rp∨(q∨r)

4. zaprzeczenie implikacji ∼(p=>q)[p∧(∼q)]

5. przechodności implikacji [(p=>q)∧(q=>r)]=>(p=>r)

Prawa de'Morgana:

1. zaprzeczenie koniunkcji ∼(p∧q)[∼p∨(∼q)]

2. zaprzeczenie alternatywy ∼(p∨q)[∼p∧(∼q)]

Podmiotem w zdaniu może być:

Nazwa ogólna np.: rzeka, miasto;

Nazwa jednostkowa np.: Wisła, Warszawa;

Zmienna x,y,z

Zdanie, w którym występuje zmienna nazywamy funkcją zdaniową lub formą zdaniową. Funkcja zdaniowa ( forma zdaniowa ) z jedną zmienną określoną na zbiorze A, jest to takie wyrażenie zawierające tę zmienną, które staje się zdaniem, gdy w miejsce zmiennej podstawimy dowolny element zbioru A.

Zbiór A nazywany też jest dziedziną D funkcji zdaniowej lub zakresem tej zmiennej.

p(x), q(x), f(x), .. oznaczenia funkcji zdaniowych zmiennej x.

q(y), r(z) zmiennych y, z

Klasyfikacja form zdaniowych:

• klasa P: formy zdaniowe spełnione przez wszystkie elementy zbioru A, wartości zmiennej x.

• klasa F: formy zdaniowe, które nie są spełnione porzez żaden element zbioru A, żadną wartość zmiennej x.

• Klasa T: formy zdaniowe spełnione przez niekóre lecz nie wszystkie elementy zbioru A, wartości zmiennej x.

Formy zdaniowe mogą mieć postać złożoną. Zdania atomowe, proste połączone odpowiednimi spójnikami zdaniowymi, funktorami zdaniotwórczymi:

• p∧q(x)




• p(x)∧q(x)

• p∨q(x) p(x)∨q(x)

• p=>q(x) p(x)=>q(x)

• pq(x) p(x)q(x)

• ∼p(x)

• ∼q(x)

p	q	p∧q(x)	p∨q(x)	P=>q(x)	P(x)=>q
1	P	P	P	P	P
1	F	F	P	F	P
1	T	T	P	T	P
0	P	F	P	P	F
0	F	F	F	P	P
0	T	F	T	P	T

Tabele wartości logicznych form zdaniowych:

p(x)	q(x)	P(x)∧q(x)	p(x)∨p(x)	P(x)=>q(x)	P(x)q(x)
P	P	P	P	P	P
P	F	F	P	F	F
P	T	T	P	T	T
F	P	F	P	P	F
F	F	F	F	P	P
F	T	F	T	P	T
T	P	T	P	P	T
T	F	F	T	T	T
T	T	F,T	T,P	T,P	P,T,F

Kwantyfikator ogólny: ۸

dla każdego x x

Kwantyfikator szczegółowy: ۷

dla pewnego x x

Prawa rachunków kwantyfikatorów: (pod ۷ i ۸ piszemy x)

1. ۸ [p(x)=>q(x)]=>[ ۸ p(x)=> ۸ q(x)]

2. ۸ [p(x)=>q(x)]=>[ ۷ p(x)=> ۷ q(x)]

3. ۷ [p(x)∧q(x)]=>[ ۷ p(x)∧ ۷ g(x)

4. ۷ [p(x)∨g(x)]=>[ ۷ p(x)∨ ۷ g(x)

5. ۸ [p(x)q(x)]=>[ ۸ p(x) ۸ q(x)]

Kwantyikatory o ograniczonym zakresie:

۸ ۷ ۷ ۸

x∈A x∈C x∈N x∈R

Twierdzenie:

Jeżeli w danym prawie rachunku kwantyfikatorów, nie zawierającym zmiennych wolnych, zastąpimy kwantyfikatory ۷ ۸ odpowiednio kwantyfikatorami ۷ ۸ x x

x∈A x∈a

gdzie A jest niepustym zbiorem, to tak otrzymane wyrażenie będzie również prawem rachunku kwantyfikatorów.

p(x)	۸ p(x)	۷ p(x)
	x	x
P	1	1
F	0	0
T	0	1
p(x)	p(x)∨∼p(x)		۷ [p(x)∨∼p(x)
			X
P	P		1
F	P		1
T	P		1

TEORIA MNOGOŚCI

Zbiory A, B, C, ...

x∈X x jest elementem X

x∉X x nie jest elementem X

Zbiór pusty: 0, ∅

Uniwersum: U

Działania na zbiorach:

Suma zbiorów A∪B A plus B A+B,

Iloczyn zbiorów A∩B A razy B A*B

Iloczyn kart. AxB

Różn. zbiorów A-B A minus B A\B

Różn. Symetryczna A÷B A∆B

Inkuzja zbiorów A⊂B A zawiera się w B

Negacja -A

Dopełnienie - uzupełnienie:

∅-(A) = A

-U = ∅

-∅ = U

A ∩ -A = ∅ oraz A ∪ -A = U

Suma zbiorów: A ∪ B

{x∈A∪B}{x∈A ∨ x∈B}

A ∪ B=B ∪ A

A∪A=A

(A∪B)∪C=A∪(B∪)

Iloczyn zbiorów:

{x∈A∩B}{x∈A ∧ x∈B}

A∩B = B ∩ A (przemienność)

A∩A = A

0∩A = 0

A∩B ⊂ B

A∩B ⊂ A

(A∩B) ∩ C=A ∩ (B∩C) (łączność)

Różnica zbiorów: A-B

{x∈A-B}{x∈A ∧ x∉B)

A-B ⊂ A

A-(B∩C)=(A-B) ∪ (A-C)

A-(B∪C)=(A-B) ∩ (A-C)

A-(A-B)=A∩B

Różnica symetryczna zbiorów A÷B

A÷B=(A-B)

A÷B=(A∪B)-(B∩A)

A÷0=A

(A÷B)÷C=A÷(B÷C)

A∩(B÷C)=(A∩B)÷(A∩C)

Inkluzja zbiorów A ⊂ B

(A ⊂ B)<=>(۸x∈A=>x∈B)

x

Iloczyn Kartezjański zbiorów AxB

Prawa de'Morgan'a:

1. -(A∪B) = -A ∩-B

2. -(A∩B) = -B ∪-A

A∪B=B∩A przemienność

A∩B=B∪A

(A∩B)∩C=A∩(B∩C) łączność

(A∪B)∩C=A∩(B∪C)

A∩(B∪C)=(A∩B)∪(A∩C) rozdzielność

A∩(B∩C)=(A∪B)∩(A∪C)

A∩A=A idempotentość

A∪A=A identyczność

A∩∅=∅

A∪∅=A

A∩U=A

A∪U=U

-A(-A)=A podwójna negacja

A∩-A=∅ dopełnienie

A∪-A=U

-U=∅ -∅=U

Działaniem w zbiorze niepustym A nazywamy odwzorowanie f iloczynu kartezjańskiego (AxA) zbioru A w zbiór A:

f: A x A → A

۸a • b = c gdzie (a,b) ∈AxA c∈A

a,b∈A

Działania wewnętrzne oznaczamy addytywnie lub multiplikatywnie i nazywamy odpowiednio dodawaniem lub mnożeniem.

Jeżeli określone jest jedno działanie, to oznaczamy je na ogół multipkikatywnie, a addytywnie jedynie wtedy, gdy jest to działanie przemienne.

Gdy określone są dwa działania, to jedno z nich (przemienne) oznaczamy addytywnie, a drugie (przemienne lub nie) multiplikatywnie.

Działanie zewnętrzne zawsze oznaczamy multiplikatywnie stosując wyraźnie inne oznaczenia na zbiory i operatory.

Działanie • określone w zbiorze A nazywamy przemiennym jeśli:

۸ a • b = b • a

a,b∈A

Działanie • określone na zbiorze A nazywamy łączonym jeśli:

۸ (a • b) • c = b • (a • c)

a,b,c∈A

Element e∈A nazywamy neutralnym elementem działania jeśli:

۸ e • a = a • e = a

a∈A

Element a'∈ A nazywa się elementem odwrotnym do a jesli:

۸ ۷ a • a' = a' • a = e

a∈A a'∈A

a'=a^-1

Relacją dwuargumentową jest każdy zbiór par uprządkowanych (a,b).

Wyrazenie aRb czytamy:

• elementy a i b pozostają w relacji lub

• relacja R przyprządkowuje elementowi a element b,

• a i b spełniają relacje R.

Relacje określamy jako zbiory par uprządkowanych, pary uporządkowane jakozbiory dwu elementowe

(a,b) ∈ {x,y : xRy} aRb

Pojęcie relacji moze być sprowadzone do pojecia zbioru.Przykłady:

1. xR₁y xy = x+y 2. xR₂y x² - y² = 1

Zbiory D_L(R), D_p(R), P(R) noszą nazwę odpowiednio lewą i prawą dziedziną relacji R oraz polem relacji. Lewą i prawą dziedzinę relacji nazywa się często dziedzina i przeciwdziedziną.

x∈D_L(R) ۷ [(x,y)∈R]

y

y∈D_p(R) ۷ [(x,y)∈R]

x

P(R) = D_L (R)∩D_P(R)

Relacja równoważności

R ∈ zwr (X) ۸ xRx

x∈A Relacja R jest zwrotna w zbiorze X.

R ∈ sym (X) ۸ (xRy => yRx)

x,y∈A Relacja R jest symetryczna w zbiorze X.

R ∈ przech(X) ۸ (xRy ∧ yRz => xRz)

x,y,z∈A Relacja R jest przechodnia w zbiorze X.

Funkcje:

R ∈ funkcji ۸ (xRy ∧ xRz => y = z

x,y,z∈A

R ∈ funkcji ۸ x ∈ D_L(f) => [y = f(x) x f y]

ALGEBRA

ALGEBRA

Algebra stawia sobie za cel szczegółowe badanie struktur algebraicznych rozmaitych typów. Wybór tych typów podyktowany jest z jednej strony potrzebami innych działów matematyki, a z drugiej wewnętrzną logiką i budowa samej algebry.

Odwzorowanie iloczynu kartezjańskiego FxA w zbiór A nazywamy działaniem zewnętrznym określonym w zbiorze A.

F x A → A

Niech x∈F oraz a∈A. Działaniem zewnętrznym jest odwzorowanie g podporządkujace każdej parz (x,a) ściśle określony element zbioru A, który oznaczamy g(x,a) lub xa.

Podporządkowanie x→xa jest odwzorowaniem zbioru A w siebie.

Elementy zbioru F nazywamy operatorami a zbiór F zbiorem operatorów.

Strukturą algebraiczną określoną na zbiorz A nazywamy każdy zespół (A,F₁...F_m, h₁...,h_m, g₁...g_m) złożony ze zbioru A, z pewnej ilości działań wnętrznych:

h₁: AxA→A........h_n: AxA→A

i pewnej ilości działań zewnętrznych:

g₁: F₁ xA'→A, .......g_m :F_m xA' → A

Na ogół każde z działan h₁....h_n oraz g₁...g_m spełnia szereg warunków takich jak przemienność, łączność, istnienie elementu neutralnego, istnienie elementów odwrotnych itp.

Także na zbiorach operatorów F₁....F_m mogą być określane struktury algebraiczne.

Zespół tych warunków i związków wewnętrznych i zewnętrznych określa typ struktury algebraicznej. Jest siedem głównych typów struktur algebraicznych: 1. półgrupy, 5. moduły,

2. grupy 6. przestrzenie wektor.

3. pierścienie 7. algebry

4. ciała

W czterech pierwszych sa określane tylko działania wewnętrzne w półgrupach i grupach jedno, a pierścieniach i ciałach dwa.

W trzech pozostałych:

• moduły i przestrzenie wektorowe - jedno działanie zewnętrzne obok jednego wewnętrznego w zbiorze A.

• Algebry - jedno działanie zewnętrzne obok dwóch wewnętrznych w zbiorze A.

Półgrupa:

Nazywamy zespół (A,•) złożony ze zbioru A i określonego w nim działania spełniającego prawo łączności.

(a • b) • c = a • (b • c )

Grupa:

Nazywamy zespół (A,•) złożony ze zbioru A i określonego w nim działania spełniającego następujące warunki:

• Działanie jest łączne (a • b) • c = a • (b • c )

• Istnieje w A element neutralny, jednostkowy 1. a_n=1

• Dla każdego elementu a zbioru A istnieje element odwrotny a^-1.

Pierścień:

Nazywamy zespół (A,+,•) złożony ze zbioru A i określonych w nim dwu działań, dodawania i mnożenia, o następujących własnościach:

• Dodawanie jest działaniem przemiennym i łącznym;

• Istnieje w zbiorz A element neutralny - zero - 0;

• Dla każdego elementu a zbioru A istnieje element odwrotny a^-1 = -a

• Mnożenie jest działaniem łącznym

• Mnożenie jest działaniem rozdzielnym względem dodawania.

a^-1=-a a_n=0 (a + b) • c = a • c + b • c

(a • b) • c = a • (b • c) (a + b) + c = a + (b + c)

Pierścieniem nazywamy system składający się z trójki (A;f,g) przy czym A jest zbiorem; (A;f) jest grupą; (A;g) jest półgrupą i dodatkowo zachodzi: g(f(a,b),c) = f(g(a,c), g(b,c)) oraz:

g(c,f(a,b)) = f(g(c,a),g(b,c)) dla dowolnego elementu zbioru A. Działanie nazywamy dodawaniem w piersieniu a działanie g mnożeniem.

Ciało

Nazywamy zespół (A,+,•) złożony ze zbioru A i określonych w nim dwu działań, dodawania i mnożenia przmiennego, spełniającego warunki:

• Dodawanie jest działaniem przemiennym i łącznym;

• Istnieje w zbiorze A element neutralny zero 0;

• Dla każdego a zbioru A isnieje element odwrotny -a;

• Mnozenie jest działaniem łącznym;

• Mnozenie jest działaniem rozdzielnym wdględem dodawania;

• Isnieje w zbiorze A element neutralny, jednostkowy 1, różny od zera;

• Dla każdego elementu a zbioru A-{0} istnieje element odwrotny a^-1.

a^-1=-a a_n=0 b^-1; b≠0 b_n=1

(a + b) • c = a • c + b • c

(a • b) • c = a • (b • c)

(a + b) + c = a + (b + c)

Moduł:

Nazywamy zespół (A,F,+,•) złożony ze zbioru A, z pierścienia F z dodawania w zbiorze A i z działania zewnętrznego, spełnijących nastepujące postulaty:

• Dodawanie jest działaniem przemiennym i łącznym;

• Istnieje w zbiorze A element neutralny - zerowy 0;

• Dla kazdego elementu a zbioru A istnieje element odwrotny -a.

• Działanie zewnetrzne jest rozdzielne względem dodawania w zbiorze A to znaczy dla dowolnych elementów a,b ∈ A dowolnego x ∈ F jest x • (a + b) = x • a + x • b

• działanie zewnętrzne jest rozdzielne względem dodawania w pierścieniu F, to znaczy dla dowolnych elementów x,y ∈ F i dowolnego a ∈ A jest (x + y) • a = x • a + y • a,

• dla dowolnych elementów x,y ∈ F i dowolnego a ∈ A jest (x,y)•a = x (y • a)

• w pierścieniu F istnieje elem. neutralny, jednostkowy 1, I dla każdego elementu a zbioru A jest 1 • a = a

(a + b) • x = a • x + b • x

a = 1 • a

(x + y) • a = x • a + y • a

(x y) • a = x (y • a)

a_n=1;

a^-1;

x^-1=1;

x=1;

x_n=0

Przestrzeń wektorową:

Nazywamy zespół (A,F,+,•) złożony ze zbioru A, ciała F, z dodawania określonego w zbiorze A i mnożenia zewnętrzego spełniających warunki:

• dodawanie w zbiorze A jest działaniem przemiennym i łącznym;

• istniej w zbiorz A element neutralny zerowy 0;

• dla każdego elementu a zbioru A istnieje element odwrotny -a;

• działanie zewnętrzne jest rozdzielne względem dodawania w zbiorze A, to znaczy dla dowolnych elementów a,b ∈ A dowolnego x ∈ F jest x • (a + b) = x • a + x • b;

• działanie zewnętrzne jest rozdzielne względem dodawania w ciele F, to znaczy dla dowolnych elementów x,y ∈ F i dowolnego a ∈ A jest: (x+y) • a = x • a + y • a;

• dla dowolnych elementów x,y ∈ F i dowolnego a ∈ A jest (xy) • a = x (y • a)

• w ciele F istnieje element neutralny, jednostkowy 1 taki, że dla każdego elementu a zbioru A jest 1 • a = a

Agebrą:

Nazywamy zespół (A,F,+,•, ⊗) złożony ze zbioru A i z ciała F, dwu działań - dodawania i mnożenia, określonych w zbiorze A i mnożenia zewnętrzego spełniajacego warunki:

• dodawanie jest działaniem przemiennym i łącznym;

• istnieje w zbiorze A element neutralny - zerowy 0;

• dla każdego elementu a zbioru A istnieje element odwrotny a^-1;

• działanie zewnętrzne jest rozdzielne względem dodawania w zbiorze A to znaczy dla dowolnych elementów a,b ∈ A dowolnego x ∈ F jest x ⊗ (a + b) = x ⊗ a + x ⊗ b

• działanie zewnętrzne jest rozdzielne względem dodawania w pierścieniu F, to znaczy dla dowolnych elementów x,y ∈ F i dla dowolnego a ∈ A jest (x + y)a = xa + ya;

• dla dowolnych elementów x,y ∈ F i dowolnego a ∈ A jest x(ya)=(xy)a

• w ciele F istnieje element neutralny, jednostkowy 1 taki, że dla każdego elementu a zbioru A jest 1 • a = a

• mnożenie jest działaniem łącznym;

• mnożenie jest działaniem rozdzielnym względem dodawania;

• dla dowolnych elementów a,b ∈ A i dowolnego x ∈ F jest:

a • (x ⊗ b) = (x ⊗ a) • b = x ⊗ (a • b)

Każda grupa jest półgrupą, każde ciało jest pierścieniem oraz każda przestrzeń wektorowa jest modułem.

Jeżeli w pierścieniu abstrahować od określonego w nim mnozenia i uwzględniać tylko dodawanie, to otrzymujemy zeń grupę.

Podobnie z modułu i przestrzeni wektorowej abstrahując od określonego w nich działania zewnętrznego otrzymujemy również grupy.

Z algebry otrzymuje się:

- pierścień jeżeli uwzględniać tylko działania wewnętrzne lub

- przestrzeń wektorową jeżeli uwzglednic tylko dodawanie i mnożenie zewnętrzne, a pominąc mnożenie wewnętrzne.

Mówimy z tego powodu: każdy pierścień, moduł i przestrzen wektorowa jest grupą, a każda algebra jest równocześnie i pierścieniem i przestrzenią wektorową.

Mówimy z tego powodu ze: każdy pierscień, moduł i przestrzeń wektorowa jest grupą, a każda algebra jest równocześnie pierscieniem i przestrzenią wektorową.

Dołączając do postulatów występujących w definicji

półgrupy,

grupy,

pierścienia itd.

dalsze warunki przemienności, istnienia elementów neutralnych itp., otrzymujemy specjalne typy:

półgrup,

grup,

pierścieni itd.

Za każdym razem dołączenie do przyjętych już warunków dalszych postulatów i związków między działaniami wzbogaca rozpatrywaną strukturę algebraiczną - struktura grupy przemiennej jest bogatsza od struktury

grupy, struktura pierścienia przemiennego jest bogatsza

od struktury pierścienia itd.

Przykłady grup mnożenie dodawanie

Liczby całkowite półgrupa grupa

Liczby wymierne półgrupa grupa

Liczby wymierne różne od zera grupa półgrupa

Dodatnie liczby wymierne grupa półgrupa

Ujemne liczby wymierne ------ półgrupa

Liczby +1 i -1 {+1,-1} grupa -------

Liczba 0 {0} grupa grupa

Liczba 1 {1} grupa -------

Jeżeli w półgrupie można wykonać dzielenie , to półgrupa jest grupą. Grupę ( A,f ) nazywamy grupą przemienną lub abelową jeżeli działanie f jest przemienne: tzn. dla dowolnych elementów a i b grupy A spełniona jest równość:

f(a,b) = f(b,a)

a f b = b f a

Grupę ( B; g ) nazywamy podgrupą grupy ( A; f ) jeżeli B jest podzbiorem A oraz działania g i f są takie same.

Każda grupa posiada dwie trywialne podgrupy

Podgrupą każdej grupy jest podzbiór składający się z elementu jednostkowego. Nosi on nazwę podgrupy jednostkowej. Podgrupą każdej grupy jest sama grupa.

B₁ , B₂, B₃ ….

B₁ ⊂ A

B₂ ⊂ A

Każda podgrupa podgrupy grupy jest jednocześnie podgrupą grupy.

A ⊃ B1 ⊂ B2 ⊂ B3 ⊂ ..........

Podgrupę jednostkową i samą grupę nazywamy podgrupami niewłaściwymi: wszystkie pozostałe podgrupy nazywamy podgrupami właściwymi.

Elementy, które znajdują się w każdej z dwóch lub więcej podgrup grupy, same tworzą podgrupę danej grupy. Powyższa własność podgrupy umożliwia znalezienie najmniejszej podgrupy zawierającej pewne z góry dane

elementy grupy. Wspólną część wszystkich podgrup zawierających

elementy a, b, c, ... pewnej grupy nazywamy podgrupą generowaną przez te elementy i oznaczamy ją przez { a, b, c, ....}.

GENEROWANIE ELEMENTÓW

Niech podgrupa {a, b, c, ...} zawiera np.. trzy elementy a, b, c tej podgrupy. Do tej podgrupy należy też element jednostkowy.

Na podstawie własności grupy należy do niej zaliczyć wraz z elementami a, b, c każdą ich potęgę o wykładniku będącym liczbą całkowitą oraz iloczyn tych potęg: aⁱ bⁱ cⁱ .... (przy czym i_n są liczbami całkowitymi.

GENERATRY GRUP

Podgrupa generowana przez pewne elementy jest najmniejszą podgrupą, która zawiera każdy z rozpatrywanych elementów. Jeżeli podgrupa generowana przez elementy a, b, c, ... pokrywa się z całą grupą, to mówimy, że te

elementy tworzą układ generatorów grupy. Jeśli grupa ma jednoelementowy układ generatorów, to grupę tę nazywamy grupą cykliczną.

ODWZOROWANIA

Jeżeli odwzorowanie f przyporządkowuje różnym elementom zbioru A różne elementy i każdy element zbioru A jest obrazem jakiegoś elementu, to mówimy, że f jest odwzorowaniem wzajemnie jednoznacznym lub bijekcją.

Relacja jest wzajemnie jednoznaczna wtedy i tylko wtedy, gdy jest funkcją i gdy relacja do niej odwrotna jest także funkcją.

R∈1-1=> R, R^-1 ∈ funkc

Relacja R jest wzajemnie jednoznaczna jest równoważne stwierdzeniu, że relacja jest funkcją różnowartościową.

Własności relacji wzajemnie jednoznacznej:

• 
  

• 
  

• 
  

Wzajemnie jednoznaczne odwzorowania zbioru na siebie tworzą grupę ze względu na złożenie.

DEINICJA:

Dane są: zbiór A z działaniem
oraz zbór B z

działaniem ∇ . Odwzorowanie g: A --> B nazywa się izomorfizmem , jeśli:

• g jest wzajemnie jednoznacznym odwzorowaniem, czyli funkcją różnowartościową bijekcją

• 
  

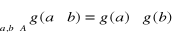
Grupa ( B;f ) jest izomorficzmym obrazem grupy ( A;f ),

gdy istnieje takie wzajemnie jednoznaczne odwzorowanie

grupy A w B , które zachowuje działanie, czyli:

• Jeśli a, b są różnymi elementami grupy A, to g(a) i g(b) są także różnymi elementami grupy B.

• Do każdego elementu a' ∂ B można znaleźć taki element a ∂ A, dla którego spełniona jest a' = g(a).

• Jeśli a' = g(a), b' = g(b) oraz c = f(a,b), to c'=f (a',b') = g(c) czyli g(f(a,b)) = f (g(a),g(b))

IZOMORIZM

Dwie grupy A i B są izomorficzne ( A ≈ B ), jeżeli pomiędzy ich elementami można ustalić wzajemno jednojednoznaczną odpowiedniość zachowaną przy działaniu grupowym.

Warunki izomrfizmu

• Różne elementy mają różne obrazy

• Każdy element jest obrazem pewnego elementu

• Zachowane są działania grupowe

MORFIZMY

Odwzorowanie spełniające jedynie warunek 3 -zachowanie działania - nosi nazwę homomorfizmu.

Odwzorowanie homomorficzne spełniające dodatkowo warunek 1 - różne elementy mają różne obrazy - nosi nazwę monomorfizmu

Odwzorowanie homomorficzne spełniające dodatkowo warunek 2 -każdy element jest obrazem pewnego elementu - nosi nazwę epimorfizmu

Istnieją cztery różne przypadki odwzorowań albo inaczej odwzorowanie homomorficzne i jego trzy specjalne odmiany:

Monomorfizm warunki 1, 3

1. 
   Różne elementy mają różne obrazy,

(3) zachowane sa działania grupowe

Epimorizm warunki 2, 3

(2). Każdy element jest obrazem pewnego elementu.

(3) Zachowane sa działania grupowe

Izomorfizm warunki 1,2,3

(1). Różne elementy mają różne obrazy

(2). Każdy element jest obrazem pewnego elementu

(3). Zachowane sa działania grupowe

ZBIORY RÓWNOLICZNE

Zbiory są równoliczne jeżeli mają tę samą ilość elementów. A rl_R B

Relacja R stwierdza równoliczność zbiorów A iB.

Warunki równoliczności:

• R ∈ 1 -1

• D_L (R) = A

• D_P (R) = B

Definicja równoliczności:

A rl_R B R ∈ 1 -1 ∧ [D₁ (R)=A] ∧ [D_P (R) = B]

Relacja równoliczności jest zwrotna, symetryczna i przechodnia w każdej rodzinie zbiorów:

A rlR A

A rlR B => B rlR A

A rlR B ∧ B rlR C => A rlR C

Relacja równoliczności jest relacją równoważności w każdej rodzinie zbiorów:

Równoliczność dwóch zbiorów A i B można sprawdzić dwiema metodami:

• można przeliczyć z osobna obydwa zbiory i porównać wyniki przeliczeń,

• polega na utworzeniu par ( a, b ) z elementów należących do obydwu zbiorów i sprawdzeniu czy pozostaje któryś z elementów bez pary.

Ta druga metoda pozwala na uogólnienie pojęcia równoliczności na zbiory nieskończone.

Dwa zbiory są równoliczne gdy istnieje odwzorowanie wzajemnie jednoznaczne jednego zbioru w drugi.

MOC ZBIORU

Każdemu zbiorowi A przyporządkowuje się pewien obiekt zwany liczbą kardynalną lub mocą oznaczany przez =

A

Dwóm zbiorom A i B przyporządkowana jest ta sama liczba kardynalna wtedy i tylko wtedy, gdy zbiory są równoliczne:

= =

A = B (A rl_R B)

Niepusty zbiór A jest zbiorem nieskończonym wtedy i tylko wtedy gdy, zbiory A i A-{a} są równoliczne dla dowolnego jego elementu a.

Zbiór nieskończony to taki zbiór, który jest równoliczny z

pewnym swoim właściwym podzbiorem

Zbiorami skończonymi są wszystkie zbiory, które nie są zbiorami nieskończonymi.

n jest liczbą naturalną wtedy i tylko wtedy, gdy jest mocą

dowolnego zbioru należącego do rodziny zbiorów

skończonych - Sk.

Liczby kardynalne, będące mocami zbiorów nieskończonych nazywamy liczbami pozaskończonymi.

Moc zbioru wszystkich liczb naturalnych N nazywamy mocą alef zero i oznaczamy ℵ

Zbiory skonczone i zbiory o mocy ℵ nazywamy zbiorami przeliczalnymi.

Moc zbioru wszystkich liczb rzeczywistych R nazywamy kontinuum.

Istnieje wiele liczb pozaskończonych.

Zbiory uporządkowane

Relecja R porządkuje zbiór A gdy A ⊂ P (R)

Relacja porządkuje pewien zbiór gdy jest spójna, asymetryczna i przechodnia

38

-A

A

A

B

C

A

B

B

a

(a,b)

B

B

A

A

B

B

A

B

A

A

A

-A

B

-A ∩ - B

B

-A∩-B

B

A

-B

B

A

-A

B

A

-(A∪B)

B

A

(A∪B)

B

A

A

-(A∪B)

B

A

-B

B

A

(A∩B)

B

A

B₂

B₁

( A, f )

(A,f)

B₂

B₁

B

A

B

A

B

A

B

A

B

A

---