Wszystkie obliczenia wykonałem na podstawie danych.... Z pośród ujętych w tym pliku zlewni wybrałem 17, od 9 do 25. Następnie ze wszystkich charakterystyk hydrologicznych wybrałem 8, są to:

• powierzchnia zlewni,

• gęstość sieci rzecznej,

• długość zlewni,

• średnia wysokość zlewni,

• średnie nachylenie,

• wskaźnik pokrycia lasami,

• wskaźnik nieprzepuszczalności gleb,

• opad średni.

1. Model regresyjny przepływu średniego

Tablica 1.1 Wielkości wybranych charakterystyk hydrologicznych.

Lp	Powierzchnia zlewni [km^2]	Gęstość sieci rzecznej [ ]	Długość zlewni [km]	Średnia wysokość zlewni [m]	Śr. nachylenie (K.) [%]	Wsk. pokrycia lasami [ ]	Wsk. nieprzepuszcz. gleb [ ]	Opad średni [mm]	Średni przepływ [m^3/s]
1	487,800	0,500	45,000	149,300	4,610	1,200	44,000	562,0	2,370
2	635,300	0,320	50,100	168,400	2,490	1,160	45,000	611,3	3,220
3	649,800	0,470	46,300	164,500	4,880	1,260	49,000	576,0	3,420
4	846,000	0,540	55,300	161,200	3,530	1,220	44,000	564,0	4,910
5	868,300	0,770	100,500	165,000	4,050	1,140	55,000	572,0	4,750
6	913,600	0,390	71,900	183,900	4,800	1,090	50,000	595,0	4,810
7	1049,700	0,350	52,300	184,600	3,280	1,150	43,000	589,6	5,150
8	1455,600	0,770	104,000	182,500	4,510	1,180	52,000	578,0	9,700
9	1816,600	0,390	90,300	165,100	2,970	1,200	38,000	610,2	8,750
10	1978,000	0,380	74,000	180,900	2,530	1,160	43,000	597,1	9,860
11	2322,400	0,500	76,800	175,800	3,260	1,180	47,000	580,0	12,490
12	3376,500	0,430	128,700	172,400	2,170	1,200	44,000	591,8	15,870
13	3561,900	0,660	104,800	156,150	1,910	1,130	43,000	583,5	21,490
14	4061,200	0,670	130,400	151,910	1,890	1,140	41,000	581,0	24,820
15	4302,300	0,430	181,800	166,700	2,050	1,210	43,000	585,6	20,400
16	4365,100	0,550	107,300	173,600	2,430	1,220	49,000	574,0	22,260
17	6900,400	0,590	149,300	175,500	2,190	1,230	48,000	576,0	33,570

Funkcja opisująca model regresyjny przepływu średniego ma postać:

, (1.1)

gdzie:

x₁,x₂,...,x_k - charakterystyki poszczególnych zlewni - zmienne wejścia;

b₀,b₁,...,b_k - estymator , B=[b₀,b₁,...,b_k] wyznaczam ze wzoru:

, (1.2)

X - macierz powstała z danych charakterystyk z dodana pierwsza kolumną samych jedynek,

Y - wektor wyjścia - przepływ średni,

ŷ - modelowana zmienna wyjścia,

k - ilość analizowanych charakterystyk zlewni.

Po wykonaniu obliczeń otrzymałem:

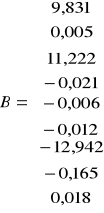
Funkcja opisująca model regresyjny przepływu średniego ma więc postać:

Sprawdziłem dodatkowo istnienie zależności
, która wynosi 207,84. Pozwala to stwierdzić, że wektor B jest dość dokładnym estymatorem wektora .

2. Przedziały ufności parametrów modelu zlewni (=0,10).

Wykorzystam tu statystykę:

(2.1)

gdzie:

b_i - kolejny element wektora B,

t_ - wartośc krytyczna z tablic t-studenta (ss=N-k-1=8, t_=1,86),

- wariancja resztkowa (wzór 2.2),

c_ii - elementy macierzy (X^TX)^-1,

_i - faktyczny parametr estymowany przez b_i.

Wzór na wariancje resztkową:

, (2.2)

która to, po potrzebnym do wzoru przekształceniu, ma wartość:

= 1,0652208

Tablica 2.1 Elementy C_ii macierzy (X^TX)^-1.

c00	540,029800000
c11	0,000000120
c22	10,244400000
c33	0,000155000
c44	0,001178000
c55	0,255547000
c66	50,997670000
c77	0,010768000
c88	0,000977000

Tablica 2.2 Obliczenia.

Lp	y	ŷ	(y-ŷ)^2
1	2,370	3,188446	0,669854
2	3,220	2,960278	0,067455
3	3,420	2,223582	1,431417
4	4,910	5,016055	0,011248
5	4,750	6,114793	1,862659
6	4,810	4,431889	0,142968
7	5,150	5,394654	0,059856
8	9,700	9,089037	0,373275
9	8,750	9,72943	0,959284
10	9,860	10,17233	0,097551
11	12,490	12,06756	0,17846
12	15,870	16,20089	0,109486
13	21,490	21,26945	0,048643
14	24,820	23,64803	1,373507
15	20,400	19,91148	0,238656
16	22,260	21,75599	0,254023
17	33,570	34,66499	1,199004
SUMA:	207,840	207,8389	9,077345

Tablica 2.3 Przedziały ufności i wektor B.

Dół		Góra
-36,2108	<β0<	55,8736
0,0045	<β1<	0,0059
4,8809	<β2<	17,5639
-0,0453	<β3<	0,0040
-0,0739	<β4<	0,0621
-1,0121	<β5<	0,9910
-27,0909	<β6<	1,2069
-0,3705	<β7<	0,0406
-0,0444	<β8<	0,0794

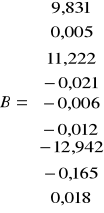
3. Weryfikacja istotności wyznaczonej funkcji regresji (=0,1)

Stosuję test:

, (3.1)

gdzie

, (3.2)

i

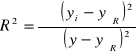
. (3.3)

Obliczone przeze mnie y_ŚR wynosi 12,226.

Testuję następującą hipotezę:

H₀: nieistotność funkcji regresji

H₁: istotność funkcji regresji

Tablica 3.1 Obliczenia.

Lp	y	ŷ	(ŷ-yśr)^2	(y-yśr)^2
1	2,37	3,188446	81,67526	97,13842
2	3,22	2,960278	85,85142	81,10592
3	3,42	2,223582	100,046	77,54356
4	4,91	5,016055	51,98161	53,52213
5	4,75	6,114793	37,34542	55,88882
6	4,81	4,431889	60,74633	54,99531
7	5,15	5,394654	46,66568	50,06811
8	9,7	9,089037	9,839797	6,380082
9	8,75	9,72943	6,232273	12,08176
10	9,86	10,17233	4,217068	5,597399
11	12,49	12,06756	0,025068	0,069758
12	15,87	16,20089	15,80066	13,27959
13	21,49	21,26945	81,7861	85,82388
14	24,82	23,64803	130,4655	158,6118
15	20,4	19,91148	59,06834	66,8162
16	22,26	21,75599	90,82302	100,6835
17	33,57	34,66499	503,5136	455,5714
SUMA:			1366,083	1375,178

Jak wynika z obliczeń:

R²=0,993387

więc:

F=150,21.

Odrzucam hipotezę o nieistotności funkcji regresji, gdyż F_KR=3,44 i jest mniejsze od obliczonej wartości F.

4. Weryfikacja istotności członów wyznaczonej funkcji regresji.

Dobór zespołu prognozującego przy zastosowaniu testu Snedecora.

Tablica 4.1 Po pominięciu jednej charakterystyki.

	bez 1	bez 2	bez 3	bez 4	bez 5	bez 6	bez 7	bez 8
B:	67,2311	53,2032	18,3584	10,0990	9,7414	-18,4130	6,0390	21,5597
		10,9544	0,0052	0,0049	0,0052	0,0052	0,0051	0,0052	0,0052
		0,0979	-0,0079	9,6683	11,4360	11,2266	13,3651	8,8091	10,4505
		0,1499	-0,0525	-0,0020	-0,0205	-0,0206	-0,0208	-0,0217	-0,0186
		-4,8237	-0,1217	-0,0318	-0,0256	-0,0060	0,0033	-0,0360	0,0006
		14,1972	-22,1914	-13,0491	-12,7597	-12,9676	-0,1683	-0,3158	-0,1100
		-0,1270	0,0076	-0,1744	-0,1748	-0,1658	-0,1637	-12,8660	-14,2895
		-0,1554	-0,0296	0,0024	0,0157	0,0177	0,0366	0,0236	-0,1721
R'^2	0,8275	0,9845	0,9914	0,9934	0,9934	0,9910	0,9916	0,9932
F	200,6240	10,8004	2,4065	0,0118	-0,0140	2,8749	2,2083	0,2619

Odrzucam współczynnik „średnie nachylenie zlewni”.

Otrzymałem model przepływu średniego z członami:

1. powierzchnia zlewni,

2. gęstość sieci rzecznej,

3. długość zlewni,

4. średnia wysokość zlewni,

5. wskaźnik pokrycia lasami,

6. wskaźnik nieprzepuszczalności gleb,

7. opad średni.

Tablica 4.2 Po pominięciu jednej charakterystyki.

	bez 1	bez 2	bez 3	bez 4	bez 5	bez 6	bez 7
B:	36,7395	52,3463	18,0943	9,8872	-20,8171	2,2218	22,3113
		13,9559	0,0053	0,0049	0,0052	0,0051	0,0054	0,0052
		0,1713	-0,0079	9,6795	11,4577	13,5039	8,5345	10,3803
		0,1588	-0,0541	-0,0024	-0,0205	-0,0209	-0,0221	-0,0184
		12,6604	-22,5286	-13,1267	-12,8144	0,0015	-0,0455	0,0001
		-0,7263	-0,0011	-0,1769	-0,1774	-0,1772	-13,7509	-14,8045
		-0,0960	-0,0272	0,0031	0,0162	0,0410	0,0327	-0,1830
R'^2	0,7177	0,9844	0,9914	0,9934	0,9909	0,9912	0,9931
F	375,9331	12,2452	2,7317	0,0317	3,3689	2,9566	0,3645

Odrzucam współczynnik „średnia wysokość zlewni”.

Otrzymałem model przepływu średniego z członami:

1. powierzchnia zlewni,

2. gęstość sieci rzecznej,

3. długość zlewni,

4. wskaźnik pokrycia lasami,

5. wskaźnik nieprzepuszczalności gleb,

6. opad średni.

Tablica 4.3 Po pominięciu jednej charakterystyki.

	bez 1	bez 2	bez 3	bez 4	bez 5	bez 6
B:	34,3962	63,2827	18,1287	-20,9482	-3,0643	22,3360
		7,6580	0,0052	0,0049	0,0051	0,0053	0,0052
		0,1796	-0,0035	9,7751	13,4511	9,1240	10,3725
		10,0190	-22,9944	-13,0656	-0,0210	-0,0216	-0,0184
		-0,4371	-0,0891	-0,1815	-0,1742	-12,3861	-14,8125
		-0,0591	-0,0540	0,0025	0,0415	0,0253	-0,1827
R'^2	0,7005	0,9822	0,9914	0,9909	0,9888	0,9931
F	442,0412	16,8827	2,9949	3,6973	6,9074	0,3685

Odrzucam współczynnik „opad średni”.

Otrzymałem model przepływu średniego z członami:

1. powierzchnia zlewni,

2. gęstość sieci rzecznej,

3. długość zlewni,

4. wskaźnik pokrycia lasami,

5. wskaźnik nieprzepuszczalności gleb.

Tablica 4.4 Po pominięciu jednej charakterystyki.

	bez 1	bez 2	bez 3	bez 4	bez 5
B:	-11,5779	21,3688	20,0904	4,9715	16,1516
		11,6417	0,0052	0,0049	0,0050	0,0053
		0,1745	-0,0065	9,6211	10,8241	7,2822
		17,7848	-17,1313	-13,3994	-0,0140	-0,0182
		-0,4209	-0,0113	-0,1823	-0,1907	-15,5500
R'^2	0,6972	0,9776	0,9914	0,9888	0,9882
F	473,8909	24,9231	2,7966	6,9326	7,9131

Odrzucam współczynnik „długość zlewni”.

Otrzymałem model przepływu średniego z członami:

1. powierzchnia zlewni,

2. gęstość sieci rzecznej,

3. wskaźnik pokrycia lasami,

4. wskaźnik nieprzepuszczalności gleb.

Tablica 4.5 Po pominięciu jednej charakterystyki.

	bez 1	bez 2	bez 3	bez 4
B:	-7,6911	20,5599	4,5114	13,9361
		34,3030	0,0051	0,0048	0,0050
		34,3943	-16,5434	10,2036	6,5433
		-0,8361	-0,0157	-0,1898	-14,1447
R'^2	0,2439	0,9773	0,9878	0,9865
F	1041,1859	19,5657	5,0481	6,8497

Taki model jest pełny, nie można już z niego usunąć żadnego nieistotnego współczynnika.

(4.1)

5. Prognoza.

Prognozuję wartość
korzystając z otrzymanej w punkcie 4 (wzór 4.1) funkcji regresji i obliczam błąd tej prognozy *
ze wzoru:

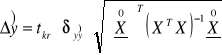
, (5.1)

w którym wykorzystuje wzór (2.2).

Na wstępie policzyłem prognozę podstawiając wartości średnie ze wszystkich 17 zlewni, otrzymałem:

=12,22

y=0,43.

Zmieniam teraz tylko jedną z charakterystyk, pozostałe są na poziomie średniej arytmetycznej dla wszystkich zlewni:

	Pow. zlewni x1		y	Gęst. sieci rzeczx2		y	Wsk. pokr. lasamx3		y	Wsk. nieprzep. gleb x4		y
min	487,8	3,23	0,66	0,32	10,4	0,86	1,09	13,4	1,05	38	13,6	1,05
max	6900,4	34,5	1,3	0,77	14,7	1,1	1,26	11,2	0,95	55	10,5	1,22

Wnioski

Z początkowo wybranych charakterystyk zlewni, po weryfikacji ich istotności, zostało tylko cztery.

Najistotniejszym współczynnikiem okazał się „powierzchnia zlewni”, dla której wartość obliczana F zawsze jest dużo większa od wartości krytycznej.

Drugim pod względem istotności współczynnikiem jest „gęstość sieci rzecznej”. Jej wartość również, przy każdej kolejnej weryfikacji, kilkakrotnie przewyższała F_KR.

Pozostałe istotne charakterystyki to wskaźniki „pokrycia lasami” i „nieprzepuszczalności gleb”.

Pozostałe, jak wynika z obliczeń, nie maja istotnego znaczenia dla wyznaczanej funkcji regresji.

Na podstawie przeprowadzonego prognozowania mogę stwierdzić, że:

• wraz ze wzrostem powierzchni zlewni przepływ średni zwiększy się. Jest to wynik mający odzwierciedlenie w rzeczywistości - im większy obszar zlewni tym więcej wody znajduje się na tym terenie;

• zachowując wielkość powierzchni, a zwiększając gęstość sieci rzecznej otrzymuję ta samą zależność - im więcej wody tym większy przepływ;

• zwiększając pokrycie terenu lasami zmniejszam przepływ średni przez zlewnię. Drzewa wykorzystują wodę, więc im ich jest więcej, tym więcej wody potrzebują do wegetacji;

• przy wzroście wskaźnika nieprzepuszczalności gleb otrzymuję zmniejszenie przepływu sredniego. Może to być spowodowane tym, że woda retencjonuje się na powierzchni gleby (np. po opadzie) i nie infiltruje wgłąb gleby, skąd zasiliłaby rzeki.

Mogę stwierdzić, że prognozowanie wykonane przeze mnie ma potwierdzenie w naturze, jest ono więc według mnie wiarygodne.

---