Laboratorium z Fizyki CMF PŁ

Dzień 15.01.2012r. godzina 18:15 grupa 1A2

Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki

semestr 1 rok akademicki 2011/2012

ocena _____

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie sie ze zjawiskiem dyfrakcji elektronów oraz pomiarem odległości międzypłaszczyznowych w polikrystalicznym graficie. Naszym zadaniem był pomiar średnicy okręgów w zależności od zmiany napięcia anodowego w przedziale od 4 kV do 9 kV, ze skokiem 0,4 kV.

Do wykonania ćwiczenia został wykorzystany układ widoczny na rysunku poniżej.

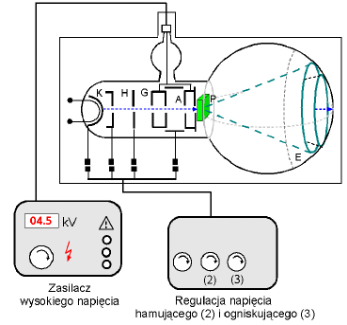
W szklanej lampie próżniowej znajdują się:

1. K - katoda (źródło elektronów)

2. H - cylinder Wehnelta (regulacja

natężenia wiązki elektronów)

3. G - elektrody ogniskujące wiązkę

4. A - anoda

5. P - grafit polikrystaliczny

6. E - ekran pokryty luminoforem

Do pomiaru średnicy okręgów widzianych na szklanej lampie próżniowej wykorzystaliśmy dostępną w zestawie ćwiczeniowym specjalną linijkę z miękkiego elastycznego materiału.

2. Wyniki pomiarów

Napięcie anodowe [kV]	Średnica I okręgu [mm]	Średnica II okręgu [mm]
4	22	42
4,5	21	40
5	21	37
5,5	21	35
6	19	34
6,5	19	33
7	18	32
7,5	17	31
8	17	29
8,5	16	28
9	15	28

3. Obliczenia (sin4Θ; Θ; sinΘ)

3a) Tabela wyników:

Obliczanie sin Θ następowało według następującego schematu:

• sin4 Θ=D/2R (gdzie D to średnica danego okręgu a R promień lampy (R=65 mm))

• 4 Θ i Θ

• sin Θ

Obliczenia dotyczące okręgów węższych	Obliczenia dotyczące okręgów szerszych
UA=4kV
sin 4Θ = 22/2*65 = 0,1846 4Θ =10˚40' Θ ≈ 2˚40' sin Θ ≈ 0,0467	sin 4Θ = 42/2*65 = 0, 3305 4Θ = 19˚48' Θ ≈ 4˚57' sin Θ ≈ 0,0863
UA=4,5kV
sin 4Θ = 21/2*65 = 0,1692 4Θ =9˚45' Θ ≈ 2˚26' sin Θ ≈ 0,0425	sin 4Θ = 40/2*65 = 0,3076 4Θ = 17˚54' Θ ≈ 4˚28' sin Θ ≈ 0,0780
UA=5kV
sin 4Θ = 21/2*65 = 0,1615 4Θ =9˚18' Θ ≈ 2˚21' sin Θ ≈ 0,0410	sin 4Θ = 37/2*65 = 0,300 4Θ = 17˚28' Θ ≈ 4˚22' sin Θ ≈ 0,0761
UA=5,5kV
sin 4Θ = 21/2*65 = 0,1538 4Θ =8˚51' Θ ≈ 2˚13' sin Θ ≈ 0,0386	sin 4Θ = 35/2*65 = 0,2796 4Θ = 16˚05' Θ ≈ 4˚01' sin Θ ≈ 0,0700
UA=6kV
sin 4Θ = 19/2*65 = 0,1462 4Θ =8˚24' Θ ≈ 2˚06' sin Θ ≈ 0,0366	sin 4Θ = 34/2*65 = 0,2692 4Θ =15˚37' Θ ≈ 3˚54' sin Θ ≈ 0,0680
UA=6,5kV
sin 4Θ = 19/2*65 = 0,1462 4Θ =8˚24' Θ ≈ 2˚06' sin Θ ≈ 0,0366	sin 4Θ = 33/2*65 = 0,2538 4Θ =14˚42' Θ ≈ 3˚40' sin Θ ≈ 0,0640

UA=7kV
sin 4Θ = 18/2*65 = 0,1384 4Θ =7˚57' Θ ≈ 1˚59' sin Θ ≈ 0,0346	sin 4Θ = 32/2*65 = 0,2461 4Θ =14˚15' Θ ≈ 3˚34' sin Θ ≈ 0,0622
UA=7,5kV
sin 4Θ = 17/2*65 = 0,1307 4Θ =7˚30' Θ ≈ 1˚52' sin Θ ≈ 0,0326	sin 4Θ = 31/2*65 = 0,2307 4Θ =13˚20' Θ ≈ 3˚20' sin Θ ≈ 0,0583
UA=8kV
sin 4Θ = 17/2*65 = 0,1230 4Θ =7˚04' Θ ≈ 1˚46' sin Θ ≈ 0,0308	sin 4Θ = 29/2*65 = 0,2230 4Θ =12˚54' Θ ≈ 3˚13' sin Θ ≈ 0,0561
UA=8,5kV
sin 4Θ = 16/2*65 = 0,1230 4Θ =7˚04' Θ ≈ 1˚46' sin Θ ≈ 0,0308	sin 4Θ = 28/2*65 = 0,2153 4Θ =12˚27' Θ ≈ 3˚08' sin Θ ≈ 0,0547
UA=9Kv
sin 4Θ = 15/2*65 = 0,1153 4Θ =6˚37' Θ ≈ 1˚39' sin Θ ≈ 0,0288	sin 4Θ = 28/2*65 = 0,2076 4Θ =12˚ Θ ≈ 3˚ sin Θ ≈ 0,0523

4. Graficzne opracowanie wyników

4a) Okręgi węższe:




	1/√ UA [V]	Sin Θ
1	0,01581	0,0467
2	0,01491	0,0425
3	0,01414	0,0410
4	0,01348	0,0386
5	0,01291	0,0366
6	0,0124	0,0366
7	0,01195	0,0346
8	0,01129	0,0326
9	0,01118	0,0308
10	0,01085	0,0308
11	0,01054	0,0288




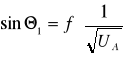
4b) Okręgi szersze:

	1/√ UA [V]	Sin Θ
1	0,01581	0,0863
2	0,01491	0,0780
3	0,01414	0,0761
4	0,01348	0,0700
5	0,01291	0,0680
6	0,0124	0,0640
7	0,01195	0,0622
8	0,01129	0,0583
9	0,01118	0,0561
10	0,01085	0,0547
11	0,01054	0,0523





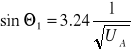
-0.005 Δa=0.14 Δb=0.008

Współczynnik korelacji 0.99222











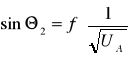
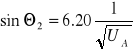
-0.012 Δa=0.18 Δb=0.002

Współczynnik korelacji 0.99637

5.Obliczenie odległości międzypłaszczyznowych d:




Gdzie:

h=6.626*10^-34 J*s

m=9,109*10^-31 kg

e=1.602*10^-`19 C

5a) Węższe pierścienie:

Dla a₁=3.24




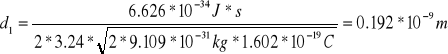
5b) Szersze pierścienie:

Dla a₂=6.20




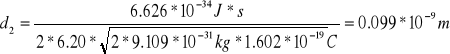
Obliczenie błędu Δd₁ metodą różniczki zupełnej

Gdzie













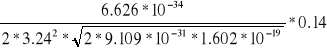
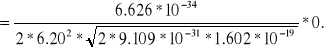
18

5. Dyskusja wyników:

5a. Błędy pomiarowe:

Na niedokładność pomiarów średnicy okręgów widzianych na szklanej lampie próżniowej wpływ miała przede wszystkim niska jakość linijki, z której ludzkie oko nie jest
w stanie odczytać dokładnych pomiarów. Poza tym pierścienie otrzymywane na ekranie nawet przy możliwości regulacji ostrości, nie były idealnie okrągłe, tak więc nie mogliśmy jednoznacznie określić ich średnic.

Kolejnym problemem na jaki natrafiliśmy podczas przeprowadzanego doświadczenia była niestabilność układu pomiarowego. Tak więc pomiary musiały być dokonywane jak najszybciej co wiąże się z możliwymi przeoczeniami.

Kolejnym aspektem wpływającym na błędy podczas opracowywania wyników była niemożność ustalenia dokładnej wartości sinusów kątów.

5b. Wnioski:

Otrzymane różniące się od siebie odległości międzypłaszczyznowe świadczą o nierównomiernym rozłożeniu płaszczyzn, jak również o różnym zorientowaniu sieci
w krysztale. Nasze wyniki międzypłaszczyznowe różnią się nieznacznie od rzeczywistych odległości wynoszących odpowiednio: 0,123 · 10^-9 m oraz 0,213 · 10^-9 m. Rozbieżność ta jest spowodowana wyżej wymienionymi błędami pomiarowymi.

Rafał Podlasek

imię i nazwisko

nr indeksu 172162

Jacek Kowalski

imię i nazwisko

nr indeksu 172157

Jarosław Jachimiak

imię i nazwisko

nr indeksu 153126

Kod ćwiczenia	Tytuł ćwiczenia
W3B	Dyfrakcja elektronów w polikrystalicznym graficie

---