I WB Gr.3 |
Gizler Kamil |
03.03.2009 |
Ćw. 1 |
Wyznaczenia przyśpieszenia ziemskiego za pomocą wahadła prostego oraz logarytmicznego dekrementu tłumienia wahadła fizycznego. |
|
Uwagi:
Teoria:
Przyśpieszenie ziemskie to swobodny spadek ciała na Ziemie. Uznano, że gdy nie występuje opór powietrza wszystkie ciała niezależne od ich kształtu, masy i składu chemicznego w tym samym punkcie na powierzchni Ziemi spadają z takim samym przyśpieszeniem.
Wahadło proste to kulka zawieszona na nieważkiej i nierozciągliwej nici .Aby wyznaczyć wartość przyspieszenia ziemskiego musimy wyznaczyć długość nici ,czas trwania 50 wahnięć oraz obliczyć okres wahań .Pomiary powtarzamy ,wyniki zestawiamy w tabeli i na podstawie wzoru na okres wahadła matematycznego
T=2Π obliczamy wartość przyspieszenia ziemskiego
Po pewnym czasie wartość wychylenia maleje wskutek tarcia i oporów powietrza .
Mamy tu do czynienia z ruchem tłumionym .Wykorzystując to zjawisko , możemy obliczyć tzw. logarytmiczny dekrement tłumienia ( jest to wielkość charakteryzująca drgania tłumione ) .Logarytmiczny dekrement tłumienia to logarytm naturalny stosunku dwóch amplitud w chwilach t i t+T .Aby wyznaczyć tą wielkość musimy odchylić wahadło od pionu i odczytywać amplitudy kolejnych wahnięć
Tabela pomiarów I
Rodzaj kuli |
Długość nici l [m] |
Średnica kuli d [m]
|
Długość wahadła L=(l+d/2) [m] |
Czas t trwania (30) okresów [s] |
Okres T [s] |
Średnia wartość okresu T [s] |
Stosunek L/T2 |
Przyśpieszenie g[m/s2] |
Metalowa I
|
0.4991 |
0.0304 0.0305 0.0306 |
0.5143 0.51435 0.5144 |
43.6 44.2 43.0 |
1.453 1.473 1.433 |
1.453 |
0.243 0.237 0.250 |
9.583 9.346 9.859 |
Metalowa II |
0.7891 |
0.0298 0.0298 0.0299 |
0.804 0.804 0.80405 |
54.2 54.2 54.4 |
1.806 1.806 1.813 |
1.808 |
0.246 0.246 0.244 |
9.701 9.701 9.622 |
Drewniana I |
0.5221 |
0.0298 0.0301 0.0301 |
0.537 0.53715 0.53715 |
44.6 44.6 44.4 |
1.486 1.486 1.480 |
1.484 |
0.2431 0.2432 0.2452 |
9.587 9.591 9.670 |
Drewniani I |
0.7751 |
0.0289 0.0284 0.0291 |
0.78955 0.7893 0.78965 |
54.4 54.4 54.6 |
1.813 1.813 1.820 |
1.815 |
0.2402 0.2401 0.2383 |
9.473 9.469 9.398 |
Tabela pomiarów II
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
An [mm] |
495 |
435 |
370 |
325 |
280 |
245 |
220 |
200 |
175 |
160 |
155 |
m=268.5g
∆m=0.5g
t=38.2; 38.0; 38.2 [s]
Błąd odczytu długości nici - 2mm
Błąd odczytu średnicy kuli - 0.1mm
Błąd odczytu czasu - 1s
Błąd odczytu amplitudy - 1cm
OBLICZENIA:
1. Wyznaczenie przyśpieszenia ziemskiego:
Okres wahań wahadła prostego ( matematycznego) określany jest następującym wzorem T=2Π. Po dokonaniu przekształceń otrzymujemy wzór na przyspieszenie ziemskie
g= 1/T2*4Π2
Wartość przyśpieszenia dla pierwszego wahadła (kula metalowa I):
g1=0.243*4*9.8596=9.583 m/s2
g2=0.237*4*9.8596=9.346 m/s2
g3=o.250*4*9.8596=9.859 m/s2
gśr=9.583+9.346+9.859/3=9.596 m/s2
Wartości przyśpieszenia dla drugiego wahadła (kula metalowa II)
g1=0,246*4*9.8596=9.701 m/s2
g2=0.246*4*9.8596=9.701 m/s2
g3=0.244*4*9.8596=9.622 m/s2
gśr=9.701+9.701+9.622/3=9.674 m/s2
Wartości przyśpieszenia dla trzeciego wahadła (kula drewniana I)
g1=0.2431*4*9.8596=9.587 m/s2
g2=0.2432*4*9.8596=9.591 m/s2
g3=0.2452*4*9.8596=9.670 m/s2
gśr=9.587+9.591+9.670/3=9.616 m/s2
Wartości przyśpieszenia dla czwartego wahadła (kula drewniana II)
g1=0.2402*4*9.8596=9.473 m/s2
g2=0.2401*4*9.8596=9.469 m/s2
g3=0.2383*4*9.8596=9.398 m/s2
gśr=9.473+9.469+9.398/3=9.446 m/s2
Średnia wartość przyśpieszenia ziemskiego wynosi:
gśr=9.583 m/s2
Odchylenia wyników poszczególnych pomiarów od wartości średniej
∆d1=│9.596-9.583│=0.013 m/s2
∆d2=│9.674-9.583│=0.091 m/s2
∆d3=│9.616-9.583│=0.033 m/s2
∆d4=│9.446-9.583│=0.137 m/s2
Błąd średni arytmetyczny wynosi:
Δ= = 0.013+0.091+0.033+0.137/4=0.0685 m/s2
Błąd średni kwadratowy wynosi:
ε= =![]()
Błąd względny pomiaru wynosi:
δ(Δ)=*100%=![]()
δ(ε)=*100%=![]()
Błąd metodą różniczki zupełnej:
![]()
g=![]()
![]()
+![]()
![]()
![]()
=![]()
![]()
![]()
=![]()
![]()
![]()
g=![]()
![]()
+![]()
![]()
Δl=2mm
ΔT==0,02s
∆g1=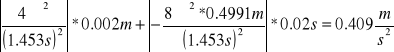
∆g2=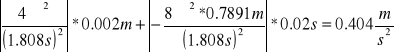
∆g3=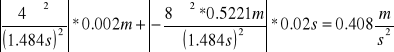
∆g4=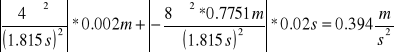
2. Wyznaczanie logarytmicznego dekrementu tłumienia:
Dekrementem tłumienia nazywamy wielkość równą logarytmowi naturalnemu ze stosunków dwóch kolejnych amplitud ![]()
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dekrement tłumienia jest wielkością stała dla danego wahadła i ośrodka. Otrzymane różnice wynikają z niemożliwości precyzyjnego odczytu amplitud poszczególnych wahnięć, dlatego jako dekrement tłumienia przyjąłem średnia arytmetyczną wartość poszczególnych dekrementów.
![]()
stąd stała tłumienia ![]()
Współczynnik oporu ośrodka jest równy ![]()
m-masa wahadła 268.5g
∆m=0.5g
t=38.2; 38.0; 38.2 [s]
![]()
![]()
![]()
3. Wnioski
Celem ćwiczenia było wyznaczenie wartości przyspieszenia ziemskiego oraz logarytmicznego dekrementu tłumienia .Uzyskana wartość przyspieszenia ziemskiego (9,583 ) nieznacznie odbiega od przyjmowanej wartości (9,81).Różnica ta może być spowodowana błędami pomiarów ,oraz tym , że wartość przyspieszenia ziemskiego nie jest stała , ale zależy od położenia punktu na powierzchni Ziemi.
Wychylenia wahadła tarczowego z położenia równowagi mają charakter gasnący. Wyznaczenie parametrów określających wielkości oporów zostało przeprowadzone w drugiej części ćwiczenia .Badane wahadło charakteryzuje się dekrementem tłumienia równym D=0,1157 .Wyliczona na jego podstawie stała tłumienia wynosi =![]()
,zaś współczynnik oporu ośrodka B=![]()
.
Wyszukiwarka