Matematyczny opis systemów
System o wielu wejściach i wyjściach (MIMO)
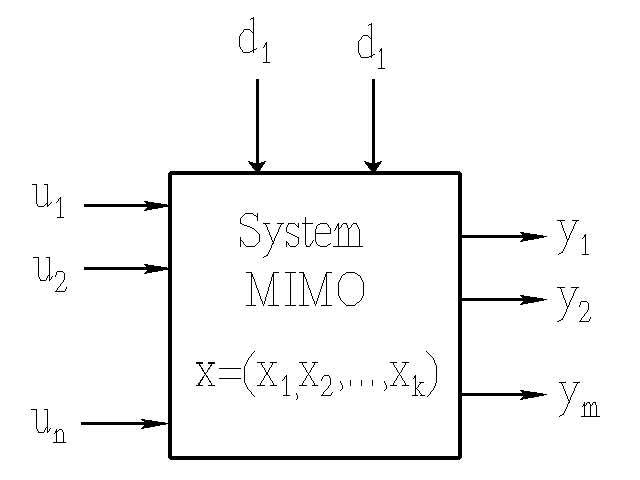
Opisywany jest przez:
u=(u1,u2,...,un) wektor wejść
y=(y1,y2,...,ym) wektor wyjść
x=(x1,x2,...,xk) wektor stanu
d=(d1,d2,...,dl) wektor zakłóceń
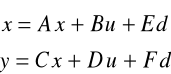
Zazwyczaj opisywany jest równaniami stanu w postaci
gdzie A, B, C, D, E, F są macierzami.
Rodzaje systemów
Skupione: Równania zależą tylko od czasu a nie od wymiarów przestrzennych. Nie rozpatrujemy rozprzestrzeniania się pól, np. fal EM.
Rozłożone: Zmienne zależą od geometrii układu i czasu.
Liniowe: Opisywane są równaniami różniczkowymi liniowymi.
Stacjonarne: Współczynniki lub macierze nie zależą jawnie od czasu.
SLS (skupione, liniowe, stacjonarne): Macierze zawierają tylko stałe.
Bez pamięci: Zmienne wyjściowe zależą tylko od aktualnej wartości zmiennych wejściowych a nie od ich wartości w poprzednich chwilach.
Przyczynowe: Skutek nie wyprzedza przyczyny, czyli sygnał wyjściowy w danej chwili nie zależy od przyszłych wartości sygnału wejściowego.
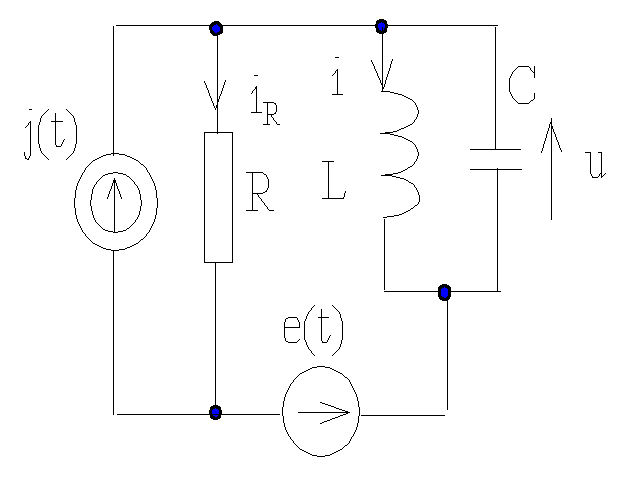
Przykład
Elementami gromadzącymi energię są L i C. Zatem zmiennymi stanu są prąd i w indukcyjności i napięcie u na pojemności.
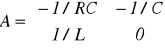
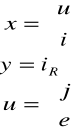
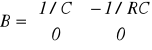
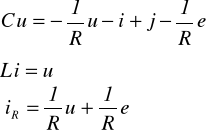
Wielkością wyjściową niech będzie iR. Równania różniczkowe mają postać
![]()
![]()
Traktując j(t) jako źródło zakłóceń (np. szumu termicznego) odpowiednio zmodyfikuj macierze. Jest to układ SLS. Gdyby R zależało od czasu, np. R=R0[1+0,2cos(ωt)] to układ jest skupiony, liniowy, niestacjonarny.
Kabel telekomunikacyjny jest układem o stałych rozłożonych.
Układy liniowe stacjonarne
Odpowiedź systemu
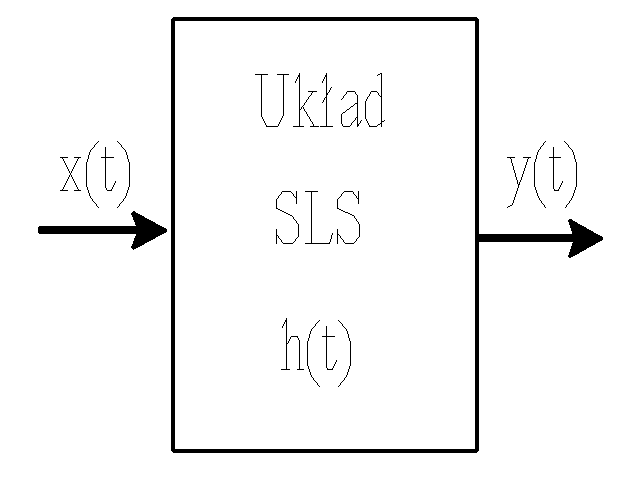
x(t) sygnał wejściowy
y(t) sygnał wyjściowy
h(t) odpowiedź impulsowa układu Odpowiedź impulsowa (na dystrybucję Diraca) określona jest następująco:
jeżeli x(t)=δ(t) to y(t)=h(t)
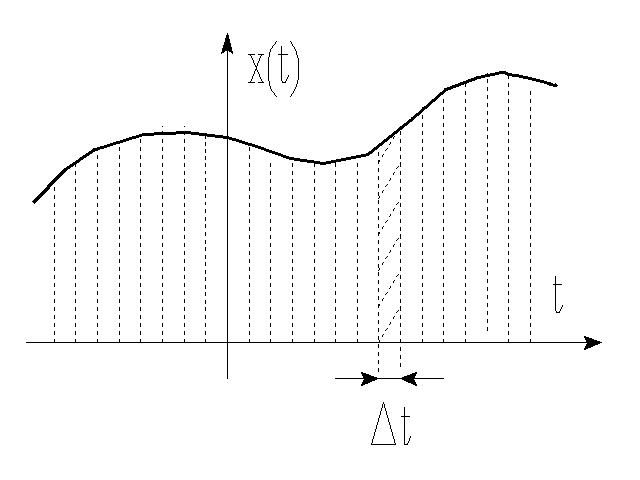
Odpowiedź na wąski impuls o szerokości Δt=tk+1-tk i wysokości x(tk) wynosi h(t)x(tk)Δt . Odpowiedź zależy tylko od odstępu czasu t-tk między przyłożeniem impulsu a chwilą obserwacji odpowiedzi (stacjonar-ność). Całkowita odpowiedź jest sumą (liniowość)
![]()
Przechodząc do granicy przy Δt→0
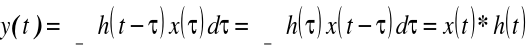
Odpowiedź układu jest splotem sygnału i odpowiedzi impulsowej układu.
Charakterystyki częstotliwościowe
Charakterystyką amplitudowo-fazową nazywamy transformatę Fouriera odpowiedzi impulsowej układu
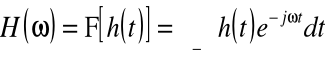
Charakterystyką amplitudową A(ω) nazywamy moduł
![]()
Jest to funkcja parzysta zmiennej ω, czyli A(ω)=A(-ω).
Charakterystyką fazową nazywamy argument
![]()
Jest to funkcja nieparzysta, czyli ϕ(ω)=-ϕ(-ω).
Charakterystyka amplitudowo-fazowa jest funkcją zespoloną zmiennej ω.
Wszystkie trzy charakterystyki nazywamy charakterystykami częstotliwoś-ciowymi.
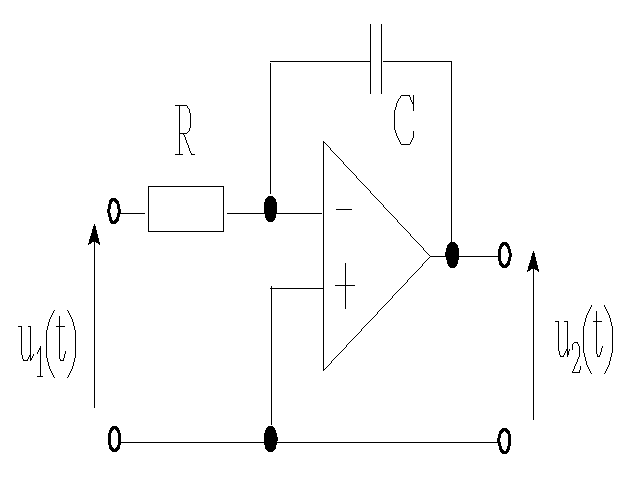
Przykład 1
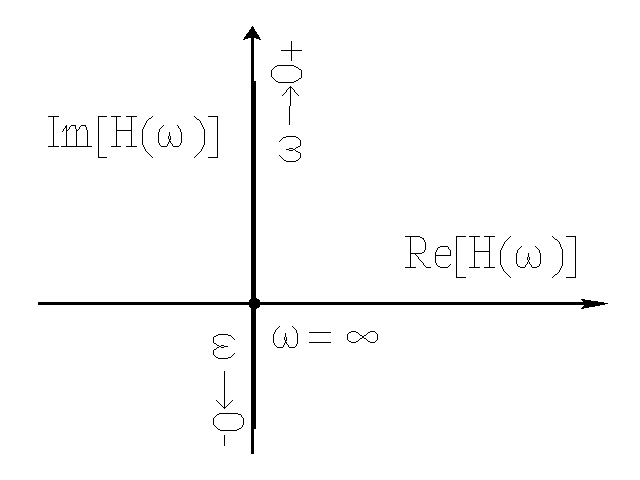
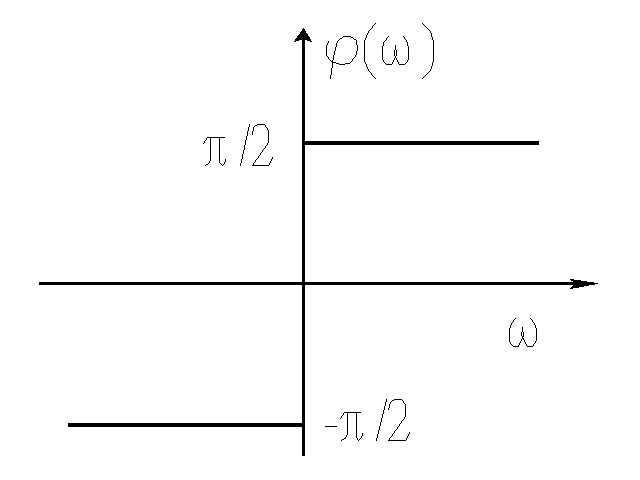
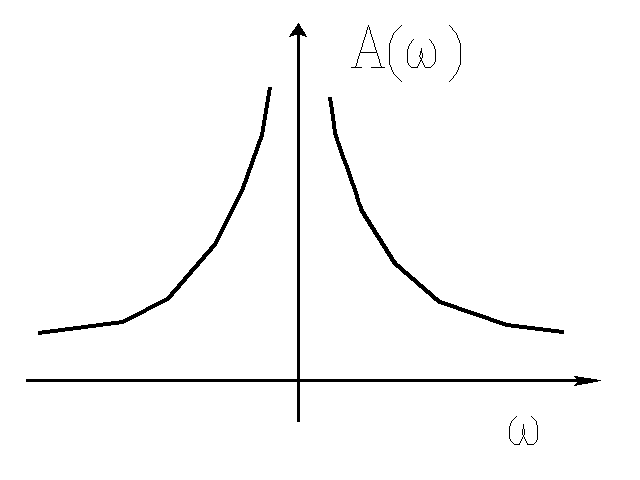
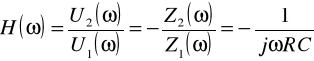
Układ całkujący z idealnym wzmacniaczem operacyjnym
Przykład 2
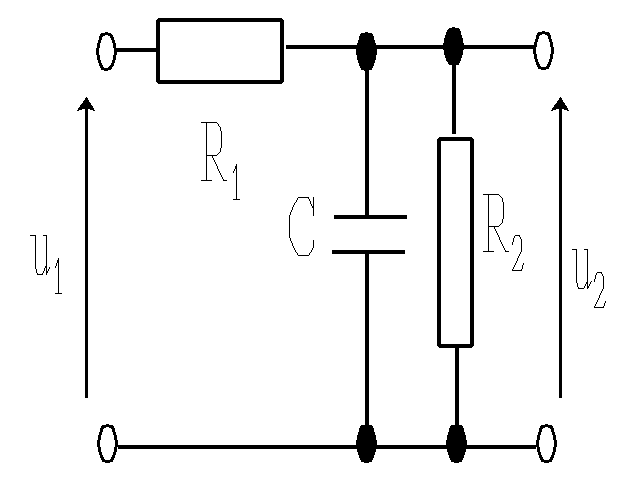
Filtr dolnoprzepustowy RC.
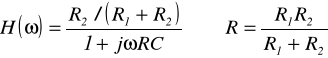
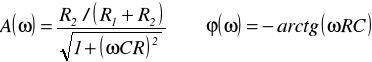
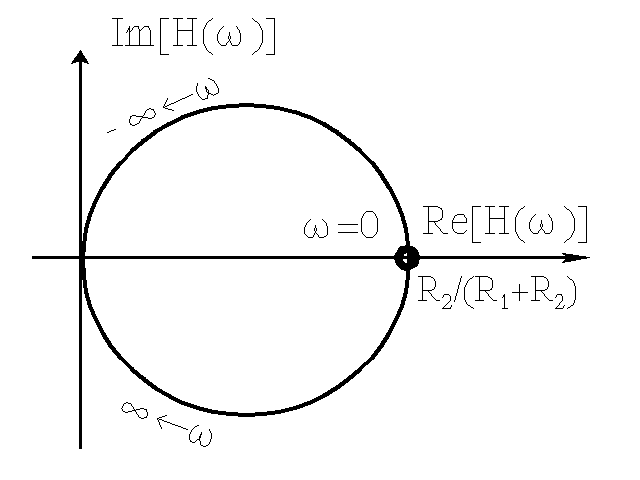
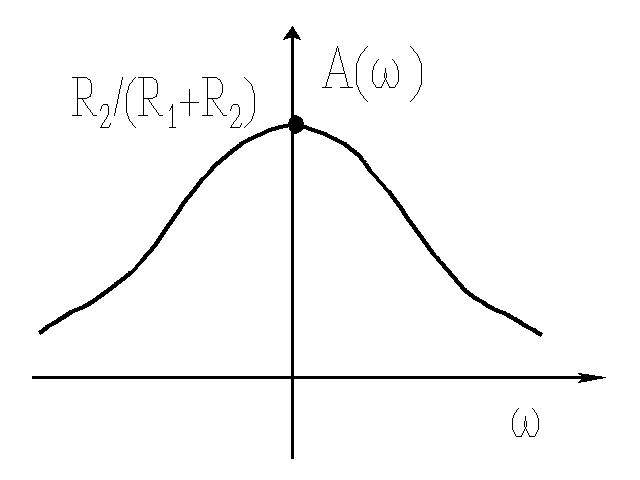
Przykład 3
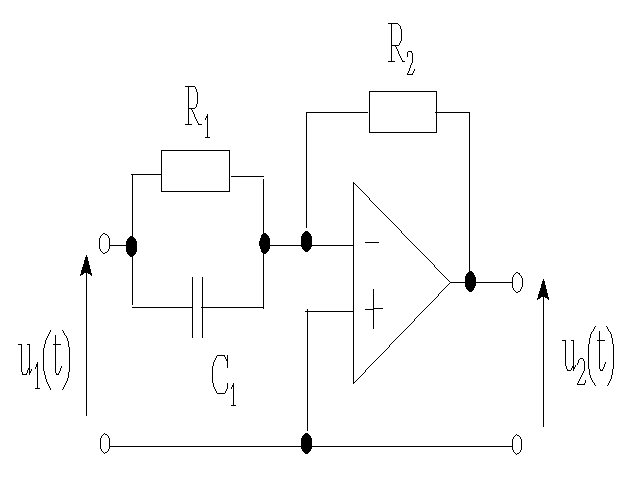
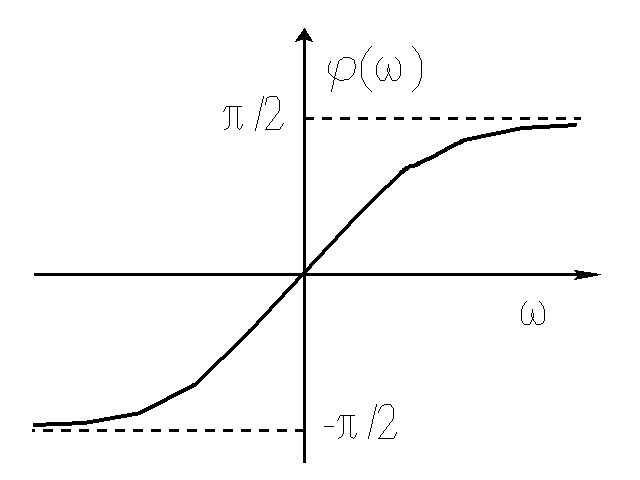
Jest to układ proporcjonalno-różniczkujący ze wzmacniaczem operacyjnym o charakterystyce
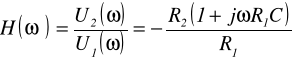
Wyznacz i narysuj wszystkie charakterystyki.
Przyczynowość
Jeżeli układ SLS jest przyczynowy to odpowiedź impulsowa h(t)≡0 dla t<0.
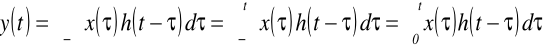
Ponadto, jeżeli x(t)≡0 dla t<0 wówczas odpowiedź y(t) przyjmuje postać
Transmitancja układu
W tej sytuacji, gdy układ SLS jest przyczynowy oraz x(t)≡0 dla t<0, wygodnie jest korzystać z przekształcenia Laplace'a
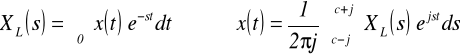
wówczas bowiem, o ile istnieją obie transformaty (Fouriera i Laplace'a), to
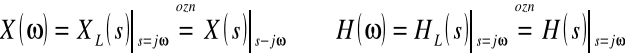
Funkcję H(s) zespolonego argumentu s nazywamy transmitancją układu.
Podstawiając s=jω dostajemy charakterystykę amplitudowo-fazową H(ω).
Z twierdzenia Borela o transformacie splotu otrzymujemy
![]()
Dla układów SLS transmitancja jest funkcją wymierną zmiennej zespolonej s
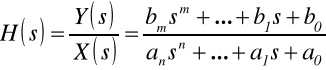
Przekształcając wyrażenie do postaci wielomianów i wyznaczając odwrotne transformaty Laplace'a otrzymujemy równanie różniczkowe układu SLS
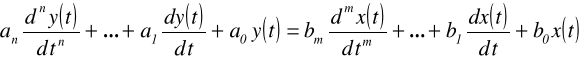
gdzie warunki początkowe są zerowe.
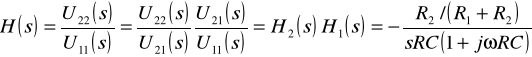
Operując transmitancjami można łatwo wyznaczać transmitancje układów złożonych. Np. dla połączenia łańcuchowego układów z przykładu 1 i 2 macierz łańcuchowa jest iloczynem [A]=[A1][A2], a ponieważ wzmacniacz operacyjny jest idealny to obciążanie go filtrem nie zmienia transmitancji napięciowej układu 1. Zatem współczynnik a11 macierzy [A] jest iloczynem współczynników a11 macierzy [A1] i [A2]. Stąd
Mianownik M(s)=ansn+...+a1s+a0 transmitancji H(s) nazywany jest wielo-mianem charakterystycznym i rozkład jego zer ma bardzo istotny wpływ na właściwości układu. Podobnie jest dla układu MIMO. Wyznaczając transformaty otrzymuje się
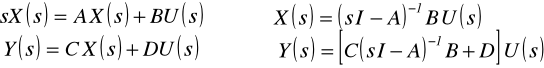
![]()
gdzie I jest jednostkową macierzą diagonalną. Wielomian charakterystyczny
SYSE_Folie Butkiewicz Bohdan
mso24E 1
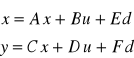
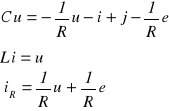
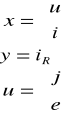
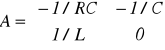
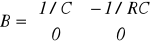
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
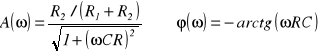
![]()
![]()
![]()
![]()
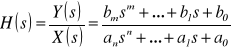
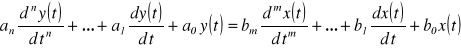
![]()
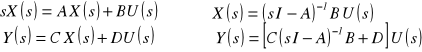
![]()
Wyszukiwarka